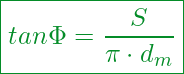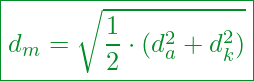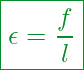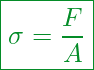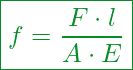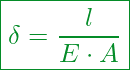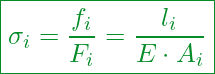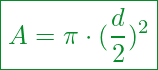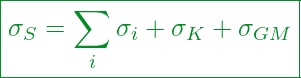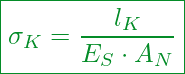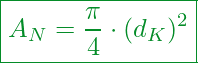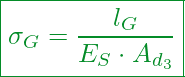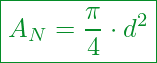Schraubenverbindung Teil 1 – Nachgiebigkeit

Grundlegendes

Die Schraubenverbindung zählt seit je her zu den wichtigsten Verbindungsarten im Maschinenbau und in der Industrie allgemein.

Speziell die Tatsache, dass es sich bei einer Schraubenverbindung um eine lösbare Verbindungsart handelt, macht sie so beliebt.

So ist es auch nicht verwunderlich, dass es sich bei Schrauben um die am meisten genutzten Verbindungselemente im Maschinenbau handelt.

Schraubenverbindung - Wichtigste Verbindungsart — Schraubenverbindung – Wichtigste Verbindungsart

Alleinstellungsmerkmal

Neben der Lösbarkeit der Verbindung, haben Schrauben selbst darüber hinaus den Vorteil, dass beinahe alle Schraubenarten weltweit genormt sind. Es ist also einfach Ersatzteile unter Kenntnis der Schraubenbezeichnung zu bestellen und das zudem zu relativ geringen Preisen und Beschaffungskosten.

Je nach Anwendungszweck kommen unterschiedlichste Schrauben zum Einsatz. Die Schraubenarten, die für uns eine besondere Relevanz besitzen, sind solche, die im Maschinenbau zum Einsatz kommen. Andere Schraubenarten, wie beispielsweise Holzschrauben, lassen wir außen vor.

Besondere Schraubenarten wie die Ösenschraube (zum Anheben von Maschinenteilen) oder das Spannschloss (Verspannen von Bauteilen wie Stahlseilen oder Drähten) sind zwar im Maschinenbau anzusiedeln aber werden auch hier nicht näher thematisiert.

Schraubenverbindung - Spannschloss — Schraubenverbindung – Spannschloss

Eine spezielle Schraubenart ist die Verschlussschraube. Diese nutzt man um Behälter (zumeist für Schmierstoffe, Öl) zu verschließen und ein Abfließen zu verhindern.

Schraubenverbindung - Verschlussschraube — Schraubenverbindung – Verschlussschraube

Beinahe alle Schraubenarten haben gemein, dass sie einen Kopf und ein Gewinde besitzen.

Abseits von diesen beiden Punkten, jedoch zeigt sich die besondere Vielfalt an Schrauben.

Schraubenbestandteile

Schraubenkopf

So ist der Schraubenkopf einer Schraube ein gutes Unterscheidungskriterium. Manche Schrauben lassen sich nur mit einem Sechkantschlüssel (innen / außen), andere nur durch einen Vielzahnschlüssel (innen / außen) einschrauben. Passt der Schraubenkopf nicht zum Werkzeug, so lässt sich kein Drehmoment erzeugen.

FUNFACT: Der INBUS-Schlüssel ist nichts anderes als der Sechskantinnenschlüssel. Hinter dem Wort INBUS steckt ein Herstellername: (- Innensechskantschraube Bauer und Schaurte)

Im Flugzeugbau kommen sehr häufig Schrauben zum Einsatz, die einen Vielzahnkopf besitzen. Denn der Vielzahnkopf erlaubt die Übertragung von sehr hohen Drehmomenten.

Gewinde

Einige Schrauben haben ein kurzes Gewinde, andere Schrauben zeichnen sich durch ein besonders langes Gewinde aus. Neben der Gewindelänge zeigen sich auch deutliche Unterschiede in der Gestaltung des Gewindes. So sind einige Gewinde sehr fein, andere Gewinde fallen eher grob aus.

Mutter

Die Mutter ist das „Gegenstück“ zu Schrauben und weist ein zum Außengewinde der Schraube passendes Innengewinde auf.

Vorteile und Nachteile eine Schraubenverbindung

+ Schrauben sind genormte Teile

+ Schraubenverbindung lässt sich lösen

+ Schraubenkräfte (Vorspannkraft) lässt sich genau einstellen

+ Schrauben und Mutter aus jeweils unterschiedlichen Materialien lassen sich paaren

+ Schrauben sind kostengünstig

+ Schrauben sind weltweit verfügbar

+ Die Herstellung einer Schraubenverbindung ist durch Laien möglich

+ Lieferzeiten für Schrauben sind vergleichsweise kurz (Lagermaterial)

– Bei der Herstellung einer Schraubenverbindung ist ein erhöhter Platzbedarf zu berücksichtigen für die Schraube und das passende Werkzeug.

– Handelt es sich nicht um eine Holzschraube, so ist die Erzeugung eines Gegengewindes zum Schraubengewinde erforderlich.

– Gegen ein Losdrehen ist die Schraube mit einer speziellen Sicherung zu sichern.

Schraubenarten

Schrauben sind nicht nur in ihrer Form vielfältig, sondern auch in Bezug auf ihren Verwendungszweck. Wir unterscheiden Schrauben als Verbindungselemente, Arbeitselemente & Stellelemente.

Verbindungselemente

Hier steht die Erzeugung von Vorspannkräften zwischen mind. zwei Bauteilen im Fokus. Daraus ergeben sich dann Reibkräfte und Dichtkräfte zwischen den Bauteilen.

Arbeitselemente

Hier nutzt man Schrauben zur Kraftwandlung mit Drehmomenten und hohen Momentübersetzungen. Der Wagenheber stellt hier ein Paradebeispiel dar.

Stellelemente

Hier steht die Bewegungswandlung in linearer Richtung im Vordergrund, zumeist ohne Kraftaufwand.

Bauformen und Verbindungsvarianten

Wie in der Abbildung zu erkennen ist, liegt hier eine dreifache Schraubenverbindung vor. Die Sechskantschrauben wurden in passende Gegengewinde innerhalb der Bauteile geschraubt. Die Reibfläche zwischen den beiden Bauteilen ist farblich markiert.

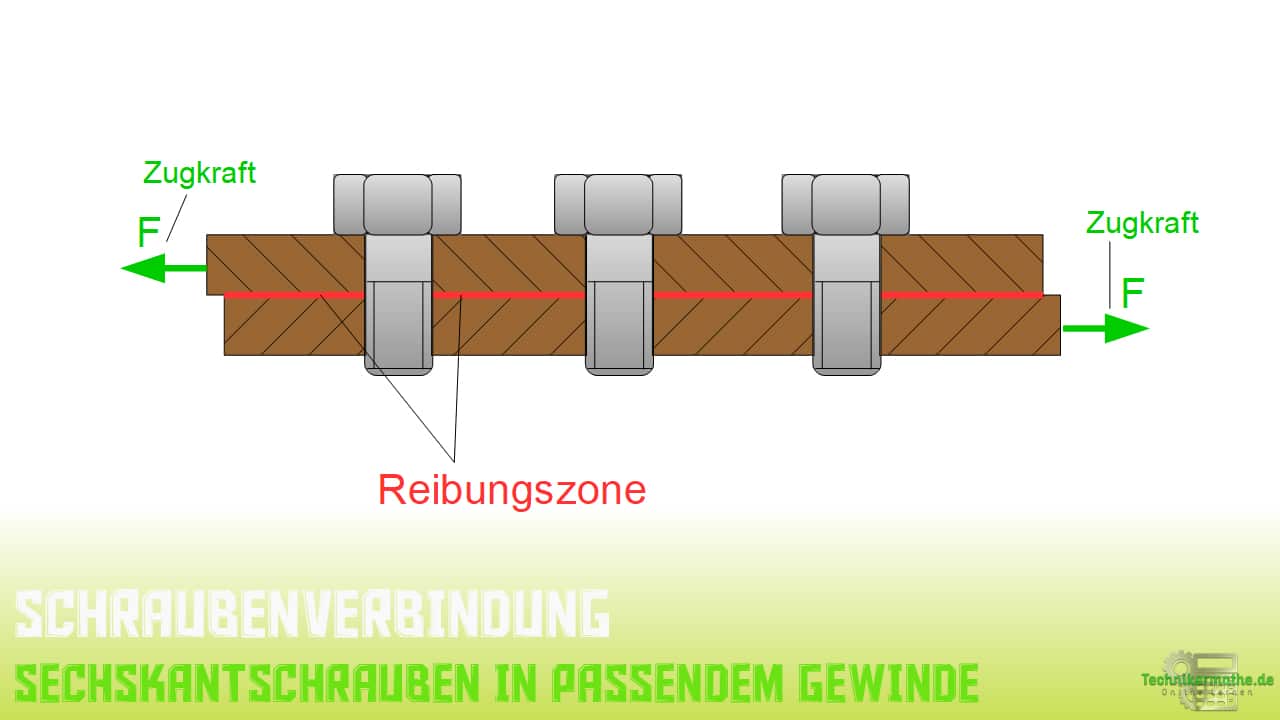
Auf dieser Fläche wirkt dann auch der Reibschluss infolge der Normalkraft, die über die Schrauben erzeugt wird (=Schraubenkraft). Wir sprechen dann von einem Kraftschluss. Ein Formschluss ist hier nicht gegeben.

Die gleiche Wirkung hat auch die Durchsteckschraube, die in der nächsten Abbildung dargestellt ist.

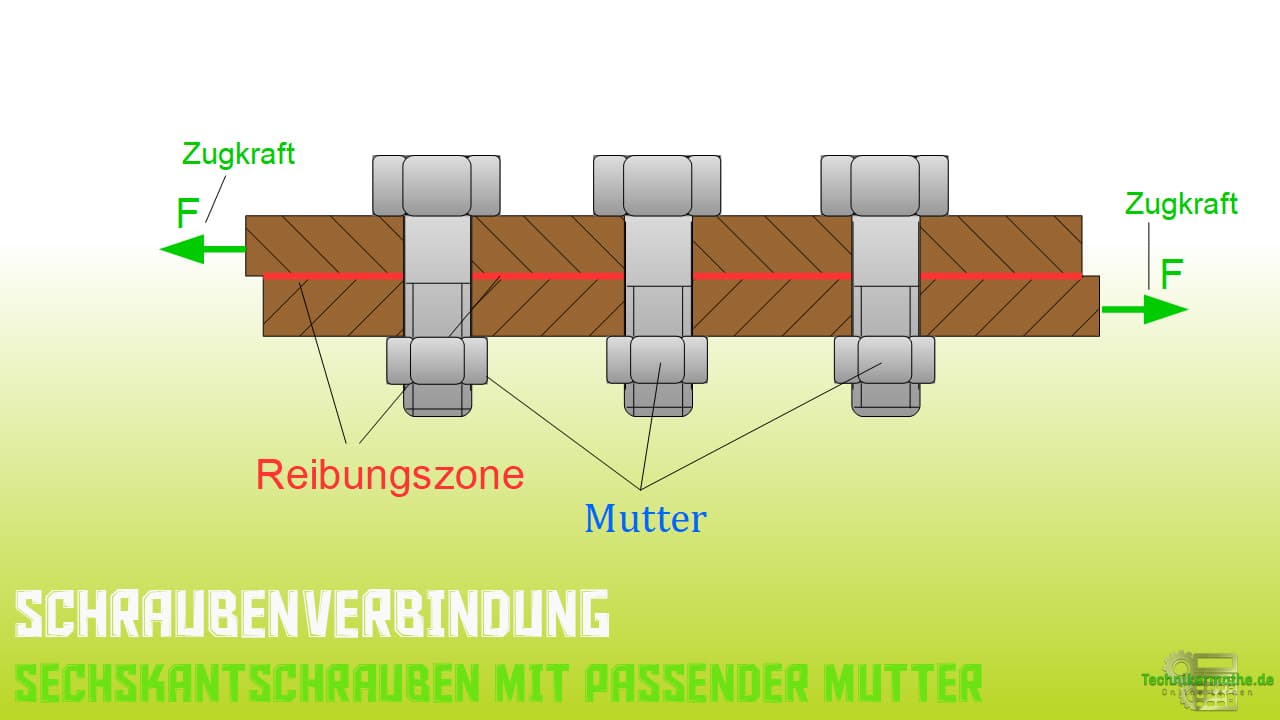
Nun haben die Bauteile jedoch keine eigenen Gewinde mehr. Das Gegengewinde der Schraube wurde über eine passende Mutter realisiert. Die Schraubenkraft erzeugt dabei wieder die Normalkraft, welche den Reibschluss zwischen den Bauteilen erzeugt.

Wir bereits oben erwähnt, existieren auch andere Schraubenarten wie das Spannschloss, welches in der nächsten Abbildung dargestellt ist.

Das Spannschloss ist sowohl Stell- als auch Arbeitselement. Als Stellelement fungiert es so lange keine Spannungen vorliegen. Sobald jedoch Spannungen auftreten, wirkt es als Arbeitselement.

Gewindearten

Dem Gewinde einer Schraube und einer Mutter (bzw. eingebrachtes Innengewinde in Bauteil) kommt eine besondere Rolle zu.

Denn nur wenn beide exakt zusammenpassen, ist es überhaupt die Herstellung der Schraubenverbindung möglich.

Unterschiedliche Gewindearten lassen sich nur selten in eine stabile Verbindung bringen.

Es gilt allgemein, dass jede Schraube am Bolzen ein Außengewinde und jede zugehörige Mutter ein passendes Innengewinde aufweist. Unterlegscheiben, die in vielen Schraubenverbindungen genutzt werden, übernehmen keine direkte Verbindungsfunktion.

Besonders außergewöhnlich ist das Gewinde der Verschlussschraube, da es ein kegeliges Feingewinde oder alternativ ein kegeliges Whitworth-Rohrgewinde. Das zugehörige Innengewinde ist hingegen zylindrisch.

Schraubenkennzeichnung

Die Schraubenkennzeichnung sieht wie folgt aus: M1, M2,…. M5, M6,…

Schraubenanforderung

Für eine passende Schraubenverbindung sind nachfolgende Kriterien zu erfüllen:

Steigungswinkel von Außen- und Innengewinde muss passen
Gewindedurchmesser von Außen- und Innengewinde muss passen
Passungen müssen berücksichtigt und eingehalten werden.
Es gilt immer Toleranzen zu berücksichtigen.

Da es sich bei Schrauben um Normteile handelt, liegen auch entsprechende Normen für das Gewindesystem vor. In diesen stehen Vorgaben für das Profil, den Durchmesser, die Steigung und die Toleranzen niedergeschrieben.

Profil: Normalgewinde, Feingewinde, Grobgewinde

Durchmesser: Gewindefuß, Nenndurchmesser, Flankendurchmesser

Steigung: Anstieg der Schraube bei einer 360° Umdrehung

Toleranzen: Angaben zu berücksichtigenden Maßen

Gewindearten – in Hinblick auf den Steigungswinkel

Um ein Gewinde eindeutig beschreiben zu können bedient man sich zweier Winkel. Wir trennen zwischen dem Steigungswinkel und dem Flankenwinkel.

Merk's dir!

Der Steigungswinkel wird immer entsprechend dem zukünftigen Einsatzzweck gestaltet. Der Flankenwinkel variiert je nach Gewindeart.

So kann eine Gewindeart unterschiedliche Steigungswinkel aufweisen, jedoch bleibt der Flankenwinkel immer gleich.

Steigungswinkel

Der Steigungswinkel $\Phi$ gibt an, wie stark das Gewinde mit einer 360° Drehung ansteigt. Gehen wir von einem regulären Gewinde aus, so beträgt der Steigungswinkel im Mittel 3°.

Man bildet bewusst den Mittelwert, da die Steigungswinkel von Innendurchmesser und Außendurchmesser des Gewindes unterschiedlich sind. Dazu bilden wir ganz einfach dem mittleren Durchmesser $d_m$ des Gewindes und lassen ihn in die Gleichung eingehen.

Für die Berechnung des Steigungswinkels verwenden wir die nachfolgende Gleichung:

$\boxed{ tan \Phi = \frac{S}{\pi \cdot d_m} }$

Kennzahlen:

$\Phi =$ Steigungswinkel

$S =$ Steigung (Ganghöhe)

$\pi =$ Kreiszahl (3,141..)

$d_m$ Mittlerer Durchmesser

Die Berechnung von $d_m$ erfolgt wie folgt:

$\boxed{ d_m = \sqrt{\frac{1}{2} \cdot (d_a^2 + d_k^2)} }$

Kennzahlen:

$d_a =$ Außendurchmesser des Gewindes

$d_k =$ Kerndurchmesser des Gewindes (= Innendurchmesser)

In der nachfolgenden Abbildung siehst du die gesuchten Größen der Gleichung nochmals eingezeichnet:

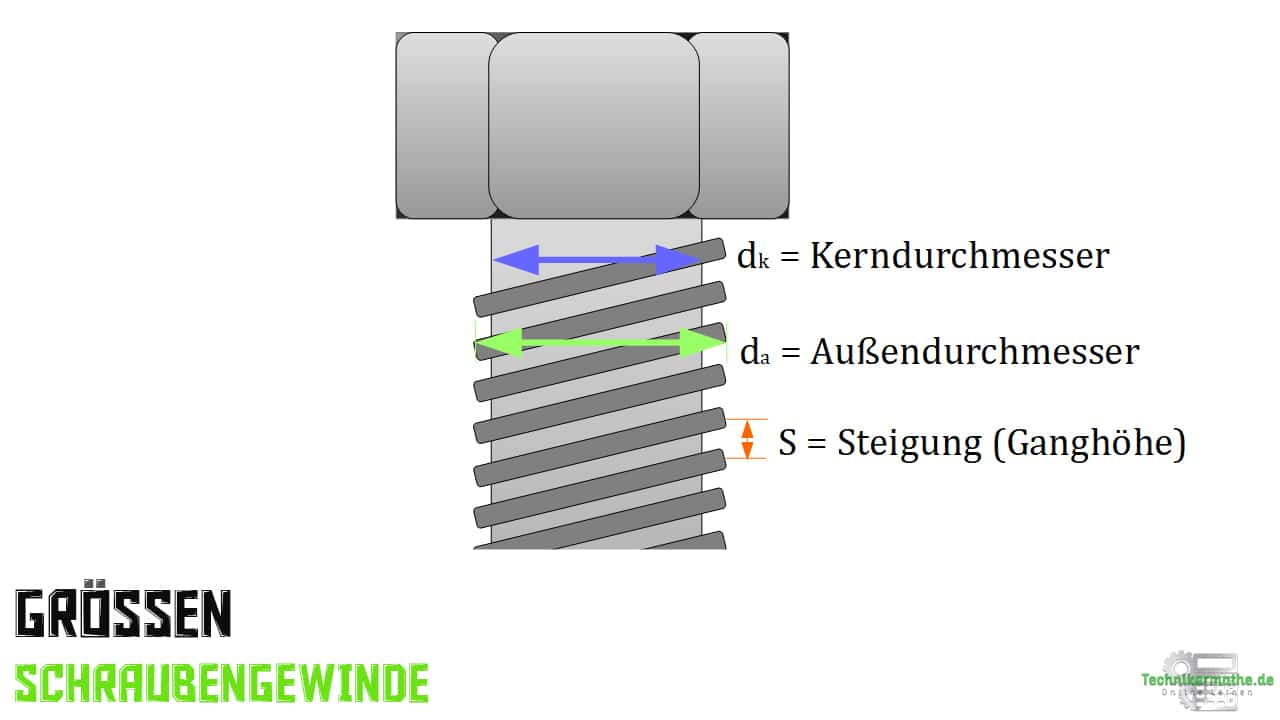
Flankenwinkel

Als zweite Winkelgröße ziehen wir den Flankenwinkel $\alpha$ heran. Der Flankenwinkel ist nichts anderes als der Winkel zwischen zwei benachbarten Flanken des Gewindes. Diese kann je nach Gewindeart unterschiedlich ausfallen. In manchen Fällen werden für ein Gewinde sogar zwei Flankenwinkel bestimmt (siehe Sägengewinde).

Aus diesem Grund siehst du in den kommenden Abbildungen exemplarisch die Darstellung von

einem Flachgewinde,
einem Trapezgewinde,
einem Sägengewinde und
einem Rundgewinde sowie
einem Spitzgewinde

inklusive den eingezeichneten Flankenwinkeln $\alpha$

Flachgewinde

Das Flachgewinde weist einen Flankenwinkel von $\alpha = 0^{\circ}$ auf.

Da das heute Anforderungsprofil für Gewinde zugenommen hat, kommt dem Flachgewinde im heutigen Maschinenbau keine spezielle Rolle mehr zu.

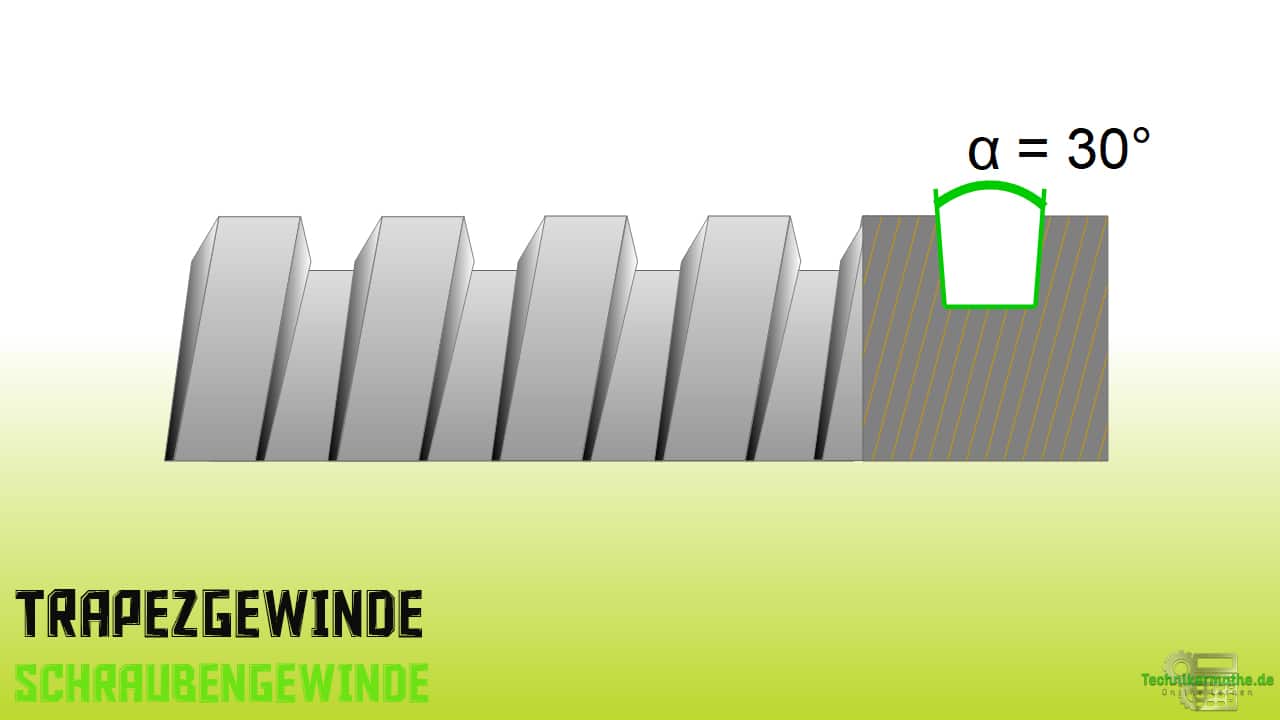
Trapezgewinde

Das Trapezgewinde besitzt einen Flankenwinkel von $\alpha = 30^{\circ}$ .

Der Vorteil dieser Gewindegestaltung liegt darin, dass es für die Ausführung von Bewegungen geeignet ist, weshalb man alternativ auch von einem Bewegungsgewinde spricht. Der Wagenheber arbeitet mit einem Trapezgewinde.

Sägengewinde

Das Sägengewinde besitzt die Besonderheit, dass hier zwei anstelle von einem Flankenwinkel angegeben werden. Die beiden Flankenwinkel betragen $\alpha = 30^{\circ}$ und $\alpha_1 = 3^{\circ}$ .

Ähnlich wie das Trapezgewinde wird es als spezialisiertes Bewegungsgewinde für eine Kraftrichtung eingesetzt, besitzt jedoch den Vorteil, dass es tragfähiger funktioniert und dadurch weniger Sprengkräfte verursacht, womit eine Schonung der zugehörigen Mutter einhergeht.

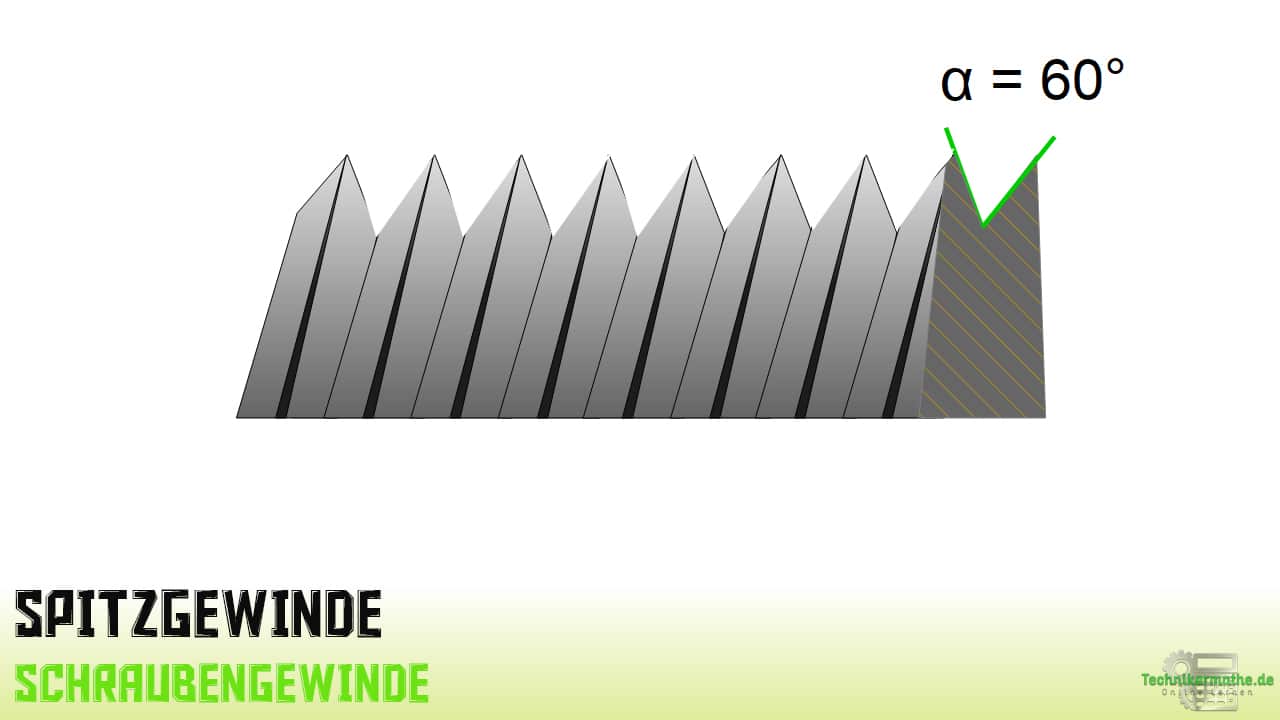
Spitzgewinde

Das Spitzgewinde besitzt mit $\alpha = 60^{\circ}$ den größten Flankenwinkel in dieser Gruppe.

Da es sich hervorragend für Verbindungen und Befestigungen eignet, wird besonders häufig im Maschinenbau eingesetzt.

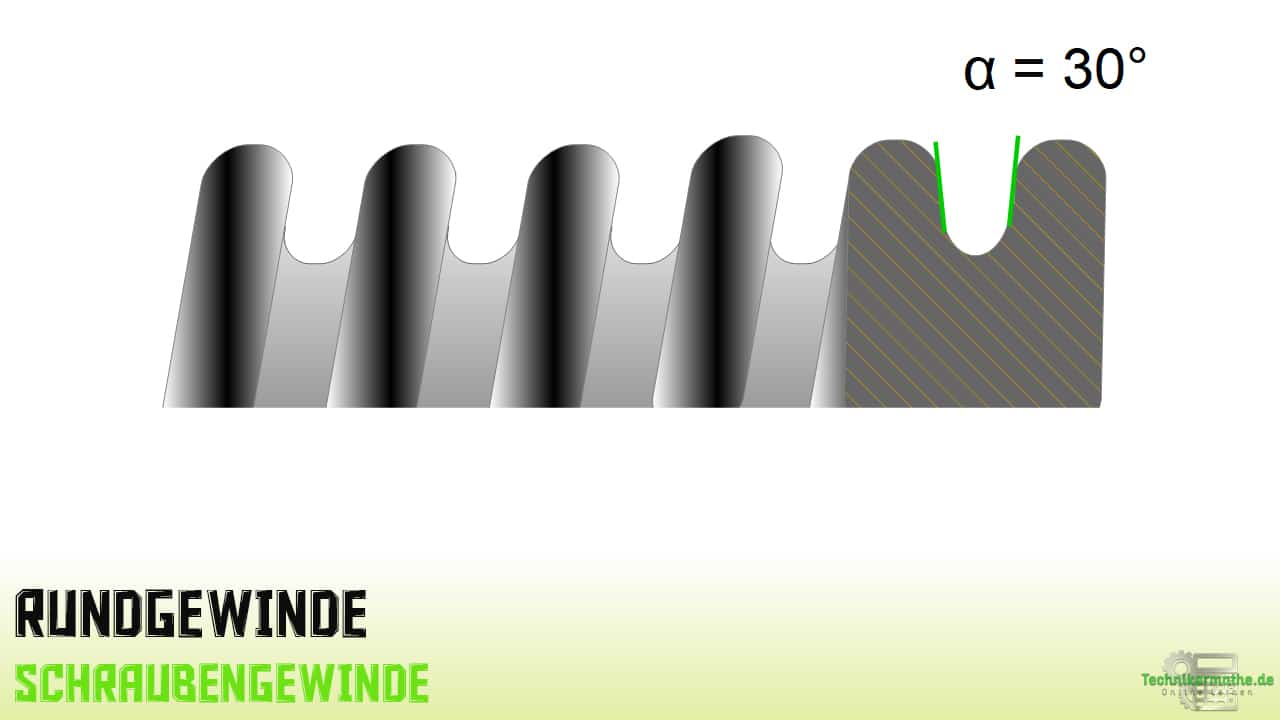
Rundgewinde

Das Rundgewinde besitzt einen Flankenwinkel von $\alpha = 30^{\circ}$

Im Gegensatz zu den anderen Gewindearten ist das Rundgewinde abgerundet, wodurch es weniger Schmutz empfindlich ist und eine geringe Kerbwirkung besitzt.

Auch die Herstellung dieser Gewindeart ist einfach und damit auch kostengünstiger.

Schraubenberechnung

Nun wenden wir uns den notwendigen Gleichungen für eine komplette Schraubenberechnung zu.

Da es unterschiedlichste Berechnungen für unterschiedlichste Schraubenarten gibt, stellen wir hier die Berechnungen für eine Befestigungsschraube vor. Die Berechnungen lassen sich aber auf andere Schraubenarten übertragen.

Befestigungsschrauben

Eine Befestigungsschraube wird immer dann eingesetzt, wenn eine vorgespannte Verbindung erzeugt werden soll. Diese Verbindung kann anschließend Betriebskräfte aufnehmen, welche in ihrer Wirklinie gleichgerichtet zur Schraubenachse verlaufen.

Je nach eingesetzten Komponenten sowie deren Nachgiebigkeit fällt die Beanspruchung der Schraubenverbindung unterschiedlich hoch aus.

Aus diesem genannten Grund ist die Kenntnis, der durch Kraft und Verformung erzeugten Zustände

die Voraussetzung für eine genaue Berechnung der erforderlichen Schraubenabmessungen.

Ausgangsgleichungen

Die nachfolgenden allgemeinen Gleichungen helfen uns für die spätere Berechnung der Nachgiebigkeit der Schraubenverbindung:

Elastische Nachgiebigkeit
Hooke’sches Gesetz

Elastische Nachgiebigkeit

Die elastische Nachgiebigkeit $\delta$ als Kehrwert der Federsteifigkeit erfasst das Verformungsvermögen eines Bauteils und kann für verschiedene Bestandteile einer Schraube ermittelt werden.

Ausgehend von der Gleichung zur Berechnung der wirkenden Kraft $F$ können wir die elastische Nachgiebigkeit durch zwei Teilschritte ermitteln.

$\boxed{ F = x \cdot c }$

Kennzahlen:

$F =$ Wirkende Kraft

$x =$ Weg

$c =$ Federsteifigkeit

Wobei gilt, dass

$x = f$ also Weg = Längenänderung

und

$c = \frac{1}{\delta}$ also Federsteifigkeit = Kehrwert der Elastischen Nachgiebigkeit

ist.

Setzen wir nun $f$ und $\frac{1}{\delta}$ stellvertretend für $x$ und $c$ ein und lösen die Gleichung nach $\delta$ auf, so erhalten wir:

$F = f \cdot \frac{1}{\delta}$

Auflösen nach $\delta$

$\delta = \frac{f}{F}$ (= Elastische Nachgiebigkeit)

Hooke’sches Gesetz

Das Hooke’sche Gesetz gibt uns Auskunft bezüglich der Relation zwischen mechanischer Spannung $\sigma$ und dem Produkt aus Elastizitätsmodul $E$ und relativer Längenänderung $\epsilon$ .

Formal sieht das wie folgt aus:

$\boxed{ \sigma = E \cdot \epsilon }$

Kennzahlen:

$\sigma =$ Mechanische Spannung

$E =$ Elastizitätsmodul [Werkstoffabhängiger Wert]

$\epsilon =$ Relative Längenänderung

Wobei die relative Längenänderung sich aus dem Quotienten von Längenänderung und Ausgangslänge errechnet.

$\boxed{ \epsilon = \frac{f}{l} }$

Kennzahlen:

$\epsilon =$ Relative Längenänderung

$f =$ Längenänderung

$l =$ Ausgangslänge

Eine andere Variante des Hooke’schen Gesetze stellt eine Relation zwischen der mechanischen Spannung $\sigma$ und dem Quotienten aus Kraft $F$ und Querschnittsfläche $A$ her.

Hier sieht die Gleichung wie folgt aus:

$\boxed{ \sigma = \frac{F}{A} }$

Kennzahlen:

$\sigma =$ Mechanische Spannung

$F =$ Wirkende Kraft

$A =$ Querschnittsfläche

In beiden Fällen zeigt sich, dass wir dir elastische Nachgiebigkeit allein durch Kenntnis von Geometriekennwerten und Werkstoffkennwerten berechnen können.

Für die Nachgiebigkeitsberechnung nehmen wir noch ein paar Anpassung an unseren bisherigen Gleichungen vor.

Zuerst setzen wir beide Varianten des Hooke’sche Gesetzes gleich:

$\sigma = E \cdot \epsilon = E \cdot \frac{f}{F}$

sowie

$\sigma = \frac{F}{A}$

Daraus ergibt sich:

$E \cdot \frac{f}{F} = \frac{F}{A}$

Anschließend lösen wir die Gleichung nach f (Längenänderung) auf und erhalten:

$\boxed{ f = \frac{F \cdot l}{A \cdot E}}$

Kennzahlen:

$f =$ Längenänderung

$F =$ wirkende Kraft

$l =$ Ausgangslänge

$A =$ Querschnittsfläche

$E =$ Elastizitätsmodul

Diese angepasste Gleichung setzen wir nun in die obige Gleichung für die elastische Nachgiebigkeit ein.

Aus

$f = \frac{F \cdot l}{A \cdot E}$

und

$\delta = \frac{f}{F} = f \cdot \frac{1}{F}$ (= Elastische Nachgiebigkeit)

wird

$\delta = f \cdot \frac{1}{F} = \frac{F \cdot l}{A \cdot E} \cdot \frac{1}{F}$

Im letzten Schritt können wir $F$ aus der Gleichung kürzen, wodurch die wirkende Kraft als Größe aus der Gleichung verschwindet.

Jetzt hängt die elastische Nachgiebigkeit lediglich von drei Größen ab.

$\boxed{ \delta = \frac{l}{E \cdot A} }$

Kennzahlen:

$\delta =$ Elastische Nachgiebigkeit

$l =$ Ausgangslänge (= Geometrischer Kennwert)

$A =$ Querschnittfläche (= Geometrischer Kennwert)

$E =$ Elastizitätsmodul (= Werkstoffabhängiger Kennwert)

Wie bereits erwähnt, gliedern wir die gesamte Schraube in ihre elastischen Teilbereiche. Damit wird die Nachgiebigkeitsberechnung der Schraube für uns einfacher und wir berücksichtigen dann auch jede spezifische Nachgiebigkeit der Teilbereiche.

Für ein besseres Verständnis schauen wir uns die nachfolgende Schraube genauer an.

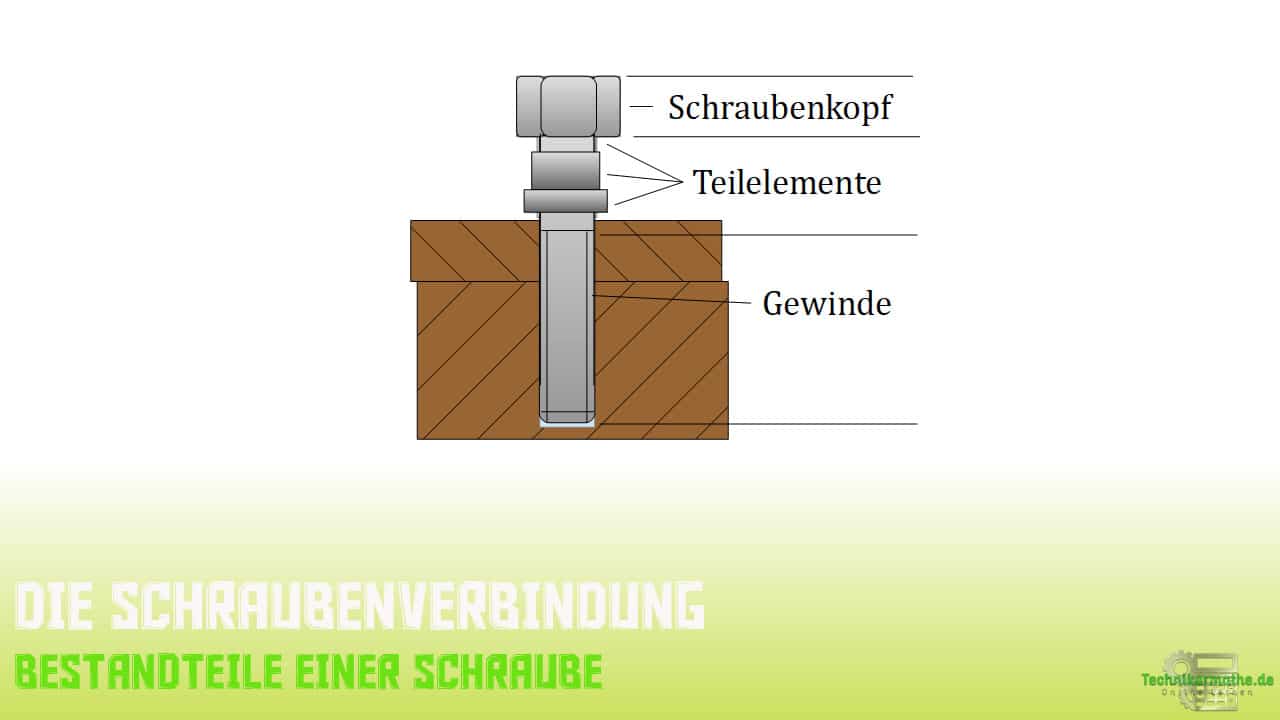
Schraubenverbindung - Schraubenbestandteile — Schraubenverbindung – Schraubenbestandteile

Es liegt uns eine Schraube mit Schraubenkopf, Teilelementen mit unterschiedlichen Durchmessern $d_i$ in verschiedenen Längen $l_i$ und dem Gewinde vor.

In der nächsten Abbildung haben wir die Durchmesser und Längen berücksichtigt.

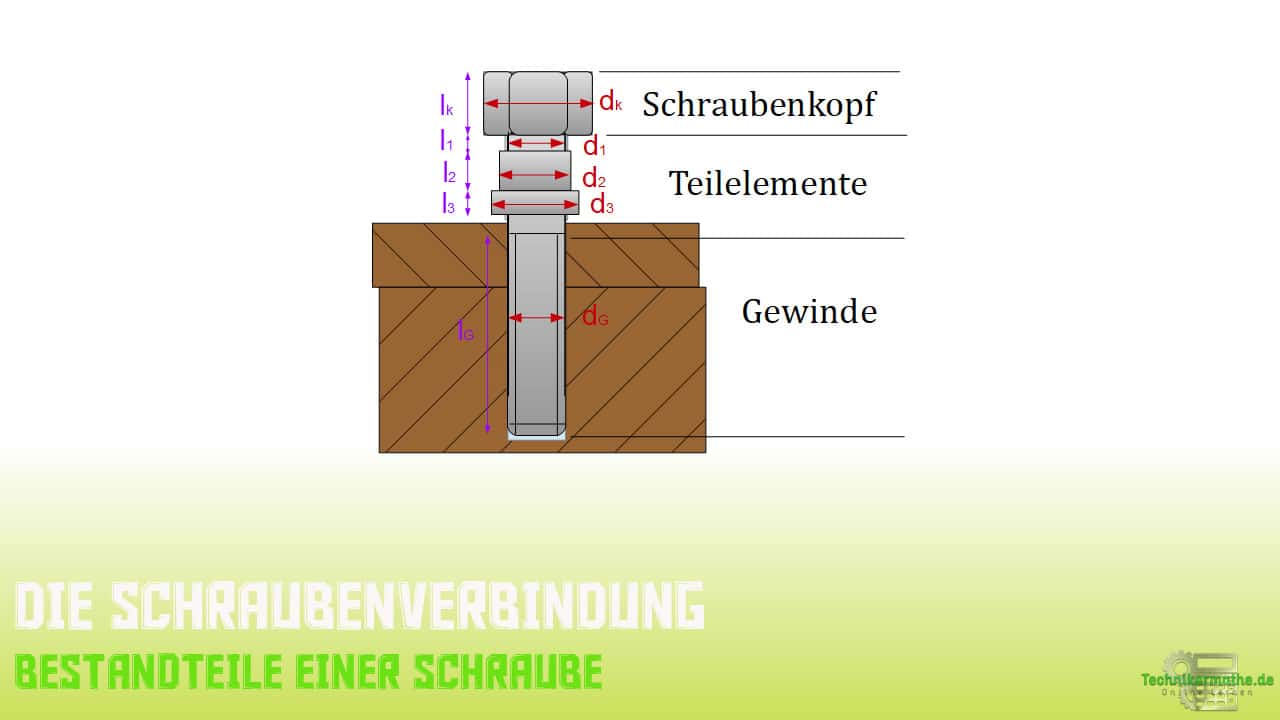
Schraubenverbindung - Bemaßung der Schraube — Schraubenverbindung – Bemaßung der Schraube

Kennen wir alle Angaben so können wir im ersten Schritt die Nachgiebigkeit der einzelnen Teilelemente mit der nachfolgenden Gleichung nacheinander berechnen:

$\boxed{ \sigma_i = \frac{f_i}{F_i} = \frac{l_i}{E \cdot A_i} }$

Kennzahlen:

$\sigma_i =$ Nachgiebigkeit eines Teilelements

$f_i =$ Längenänderung eines Teilelements

$F_i =$ Wirkende Kraft auf das Teilelement

$l_i =$ Ausgangslänge eines Teilelements

$E =$ Elastizitätsmodul des Schraubenwerkstoffes (gleichbleibend)

$A_i =$ Fläche eines Teilelements

Die Fläche eines Teilelements errechnet sich nach der bekannten Gleichung:

$\boxed{ A = \pi \cdot (\frac{d}{2})^2 }$

Oder

$\boxed{ A = \pi \cdot r^2 }$

Kennzahlen:

$A =$ Fläche

$\pi =$ Kreiszahl (3,141..)

$d =$ Durchmesser

$r =$ Durchmesser

Gesamtnachgiebigkeit der Schraube

Die Gesamtschraube können wir in drei Bereiche zerlegen und diesen Bereichen auch eine Nachgiebigkeit zuordnen:

Schraubenkopf: $\sigma_K$

Einzelne Abschnitte zwischen Schraubenkopf und Gewinde: $\sigma_i$

Gewinde (=Eingeschraubter Gewindeteil): $\sigma_{GM}$

Zusammen ergeben die einzelnen Nachgiebigkeiten dann die Gesamtnachgiebigkeit der Schraube $\sigma_S$ .

Formal sieht das dann wie folgt aus:

$\boxed{ \sigma_S = \sum_i \sigma_i + \sigma_K + \sigma_{GM} }$

Kennzahlen:

$\sigma_S =$ Gesamtnachgiebigkeit der Schraube

$\sum_i \sigma_i =$ Summe der Nachgiebigkeit der einzelnen Abschnitte

$\sigma_K =$ Nachgiebigkeit des Schraubenkopfes

$\sigma_G =$ Nachgiebigkeit des eingeschraubten Gewindeteils (= eingespannt in Mutter)

Nachgiebigkeit des Schraubenkopfes

In der nächsten Abbildung haben wir den Schraubenkopf der Schraube mit dem Durchmesser $d_K$ isoliert.

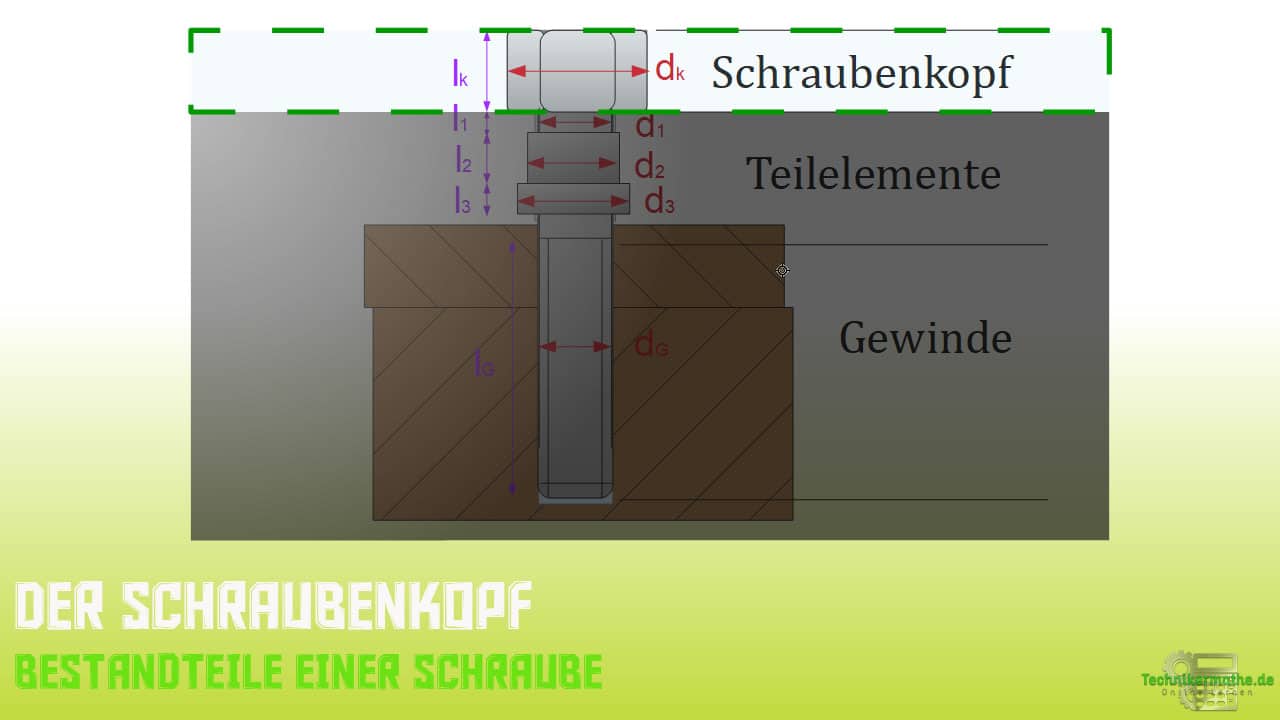
Schraubenverbindung - Schraubenkopf — Schraubenverbindung – Schraubenkopf

Die zugehörige Gleichung ist:

$\boxed{ \sigma_K = \frac{l_K}{E_S \cdot A_N} }$

Kennzahlen:

$\sigma_k =$ Nachgiebigkeit des Schraubenkopfes

$E_S =$ Elastizitätsmodul der Schraube

$A_N =$ Nennquerschnitt des Schraubenkopfes (= Aus Tabellenwerken ablesbar)

$l_K =$ Ersatzdehnlänge des Schraubenkopfes

Die Berechnung des Nennquerschnitts $A_N$ erfolgt über nachfolgende Gleichung:

$\boxed{ A_N = \frac{\pi}{4} \cdot (d_K)^2 }$

Kennzahlen:

$A_N =$ Nennquerschnitt

$\pi =$ Kreiszahl

$d_K =$ Außendurchmesser des Gewindes (Beispiel M6 = 6 mm oder M5 = 5 mm)

Die Berechnung der Ersatzdehnlänge $l_K$ hängt von der Schraubenkopfart ab:

Liegt eine Innensechskantschraube vor, dann

$\boxed{ l_K = 0,4 \cdot d_K }$

Liegt hingegen eine Sechskantschraube vor, dann

$\boxed{ l_K = 0,5 \cdot d_K }$

Kennzahlen:

$l_K =$ Ersatzdehnlänge des Schraubenkopfes

$d_K =$ Außendurchmesser des Gewindes (Beispiel M6 = 6 mm oder M5 = 5 mm)

Nachgiebigkeit des Gewindeteils

In der nächsten Abbildung haben wir den Gewindeteil der Schraube mit dem Durchmesser $d_G = d_{GM}$ isoliert.

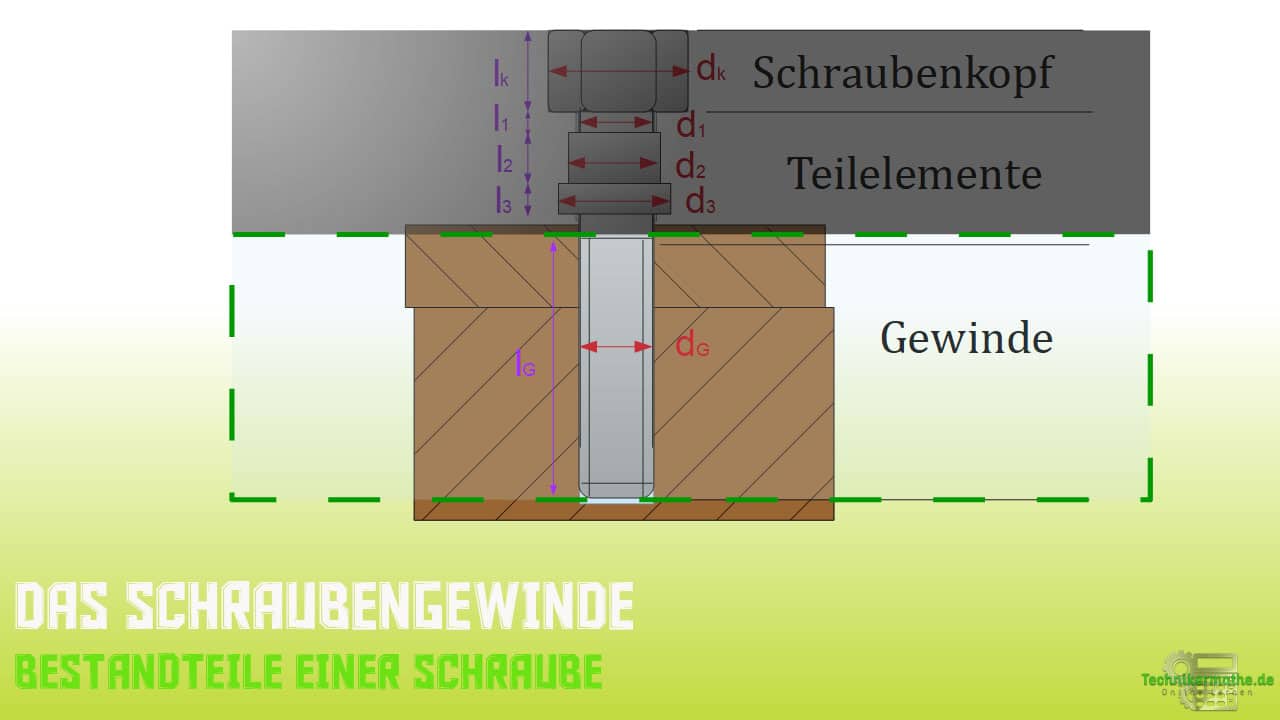
Schraubenverbindung - Schraubengewinde — Schraubenverbindung – Schraubengewinde

Wir können jetzt die bisherigen Werte verwenden um die Gleichung für die Nachgiebigkeit des eingeschraubten Gewindeteils $\sigma_{GM}$ zu formulieren.

Diese besteht zum einen aus dem Anteil für die Nachgiebigkeit des Schraubengewindekerns $\sigma_{G}$ und der Nachgiebigkeit des Einschraubgewindebereichs (Mutter) $\sigma_{M}$ .

Formal sieht das dann wie folgt aus:

$\sigma_{GM} = \sigma_{G} + \sigma_{M}$

Kommen wir nun zu der Einzelberechnung der Anteile.

Nachgiebigkeit des eingeschraubten Schraubengewindekerns

Für die Berechnung nutzen wir die nachfolgende Gleichung.

$\boxed{ \sigma_{G} = \frac{l_G}{E_S \cdot A_{d_3}} }$

Kennzahlen:

$l_G =$ Ersatzdehnlänge des eingeschraubten Schraubengewindekerns

$E_S =$ Elastizitätsmodul der Schraube

$A_{d_3} =$ Kernquerschnitt des Gewindes

$d_3 =$ Kerndurchmesser des Gewindes

Für $l_G$ gilt:

$\boxed{ l_G = 0,5 \cdot d }$

Kennzahl:

$d =$ Außendurchmesser des Gewindes

Für $A_{d_3}$ gilt:

$A_{d_3} = \frac{\pi}{4} \cdot (d_3)^2$

Nachgiebigkeit des Einschraubgewindebereichs (Mutter)

Hier unterscheiden wir zwischen einer Durchsteckschraubenverbindung / Stehbolzenverbindung und einer Einschraubverbindung / Sacklochverschraubung.

Formal gilt, dass die erste Gleichung für beide gleich ist und sieht das wie folgt aus:

$\sigma_M = \frac{l_M}{E_M \cdot A_N}$

Die einzusetzenden Größen variieren jedoch:

Größen einer Durchsteckschraubenverbindung / Stehbolzenverbindung:

$\boxed{ E_M = E_S }$

$\boxed{ l_M = 0,4 \cdot d }$

Größen einer Einschraubverbindung / Sacklochverschraubung:

$\boxed{ E_M = E_P }$

$\boxed{ l_M = 0,33 \cdot d }$

Kennzahlen:

$l_M =$ Ersatzdehnlänge der Mutter

$d =$ Außendurchmesser des Gewindes

$E_M$ Elastizitätsmodul der Schraube

$E_S =$ Elastizitätsmodul der Mutter

$E_P =$ Elastizitätsmodul des Werkstoffes des Einschraubgewindebereichs

$A_N =$ Nennquerschnitt (Wert aus Tabellenwerk)

$A_N$ kann ebenfalls berechnet werden mit:

$\boxed{ A_N = \frac{\pi}{4} \cdot d^2 }$

Nachgiebigkeit der verspannten Teile

Nachdem wir uns bisher die Schraube hinsichtlich der Nachgiebigkeit untersucht haben, folgt nun die Untersuchung der Nachgiebigkeit der verspannten Teile $\sigma_P$ .

Aber aufgepasst. Die Spannungsverteilung fällt im Bereich der Klemmung durch die Schraube nicht gleichmäßig aus, wodurch eine veränderliche Druckverteilung entsteht.

In der nächsten Abbildung siehst du erneut, die beiden Varianten der Schraubenverbindung. Links liegt eine Durchsteckverschraubung vor und rechts eine Sacklochverschraubung.

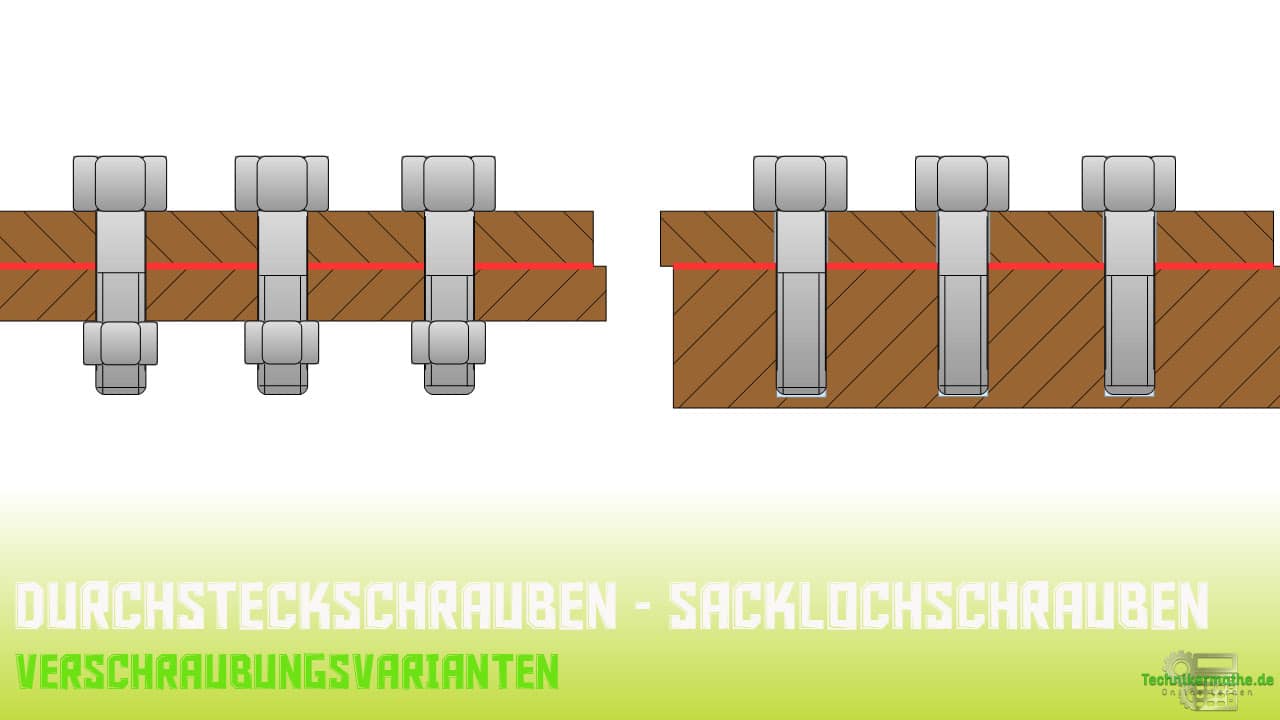
Bei beiden Ausführungen liegt eine veränderliche Druckverteilung vor:

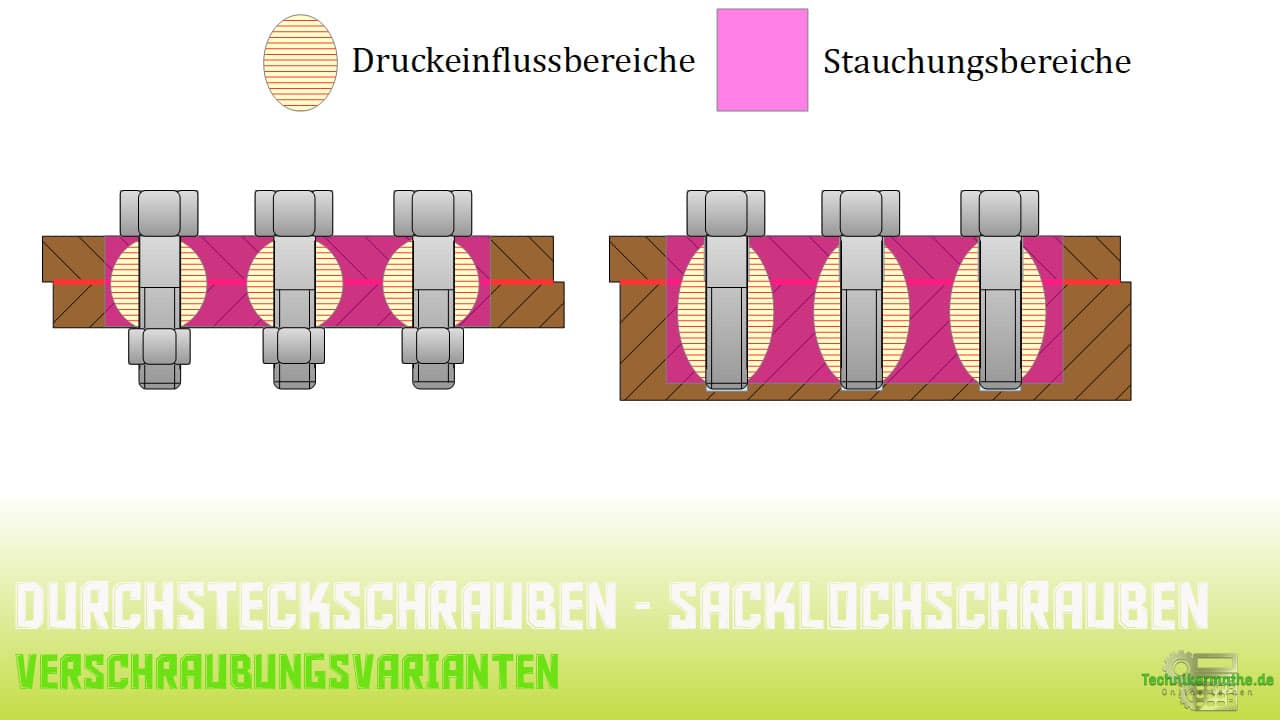
Druckeinflussbereiche - Stauchungsbereiche — Druckeinflussbereiche – Stauchungsbereiche

Die magenta umrandeten Bereiche erfahren infolge der Verschraubung eine Stauchung und müssen daher auf ihre Nachgiebigkeit hin untersucht werden.

Formal sieht das wie folgt aus:

$\boxed{ \sigma_P = \frac{f}{F} = \frac{l_K}{E_P \cdot A_{ers}} }$

Kennzahlen:

$l_K =$ Klemmlänge

$E_P =$ Elastizitätsmodul der verspannten Teile, sowie des Einschraubgewindebereichs

$A_{ers} =$ Ersatzquerschnitt

In Eurer Prüfung werden die notwendigen Größen zumeist angegeben, da eine Berechnung nur mit erhöhten Aufwand möglich ist und die rechnerische Lösung entsprechend langwierig ist.

Wie geht es weiter?...

Nachdem wir jetzt wissen, welche Berechnungen uns bei den Nachgiebigkeiten einer Schraubenverbindung begegnen können, führen wir im nächsten Schritt die Untersuchung der Schraubenverbindung im Montagezustand durch.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Übungsbereich

Demo–Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET1 (Grundlagen der Elektrotechnik) und
ET2 (Gleichstromtechnik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++