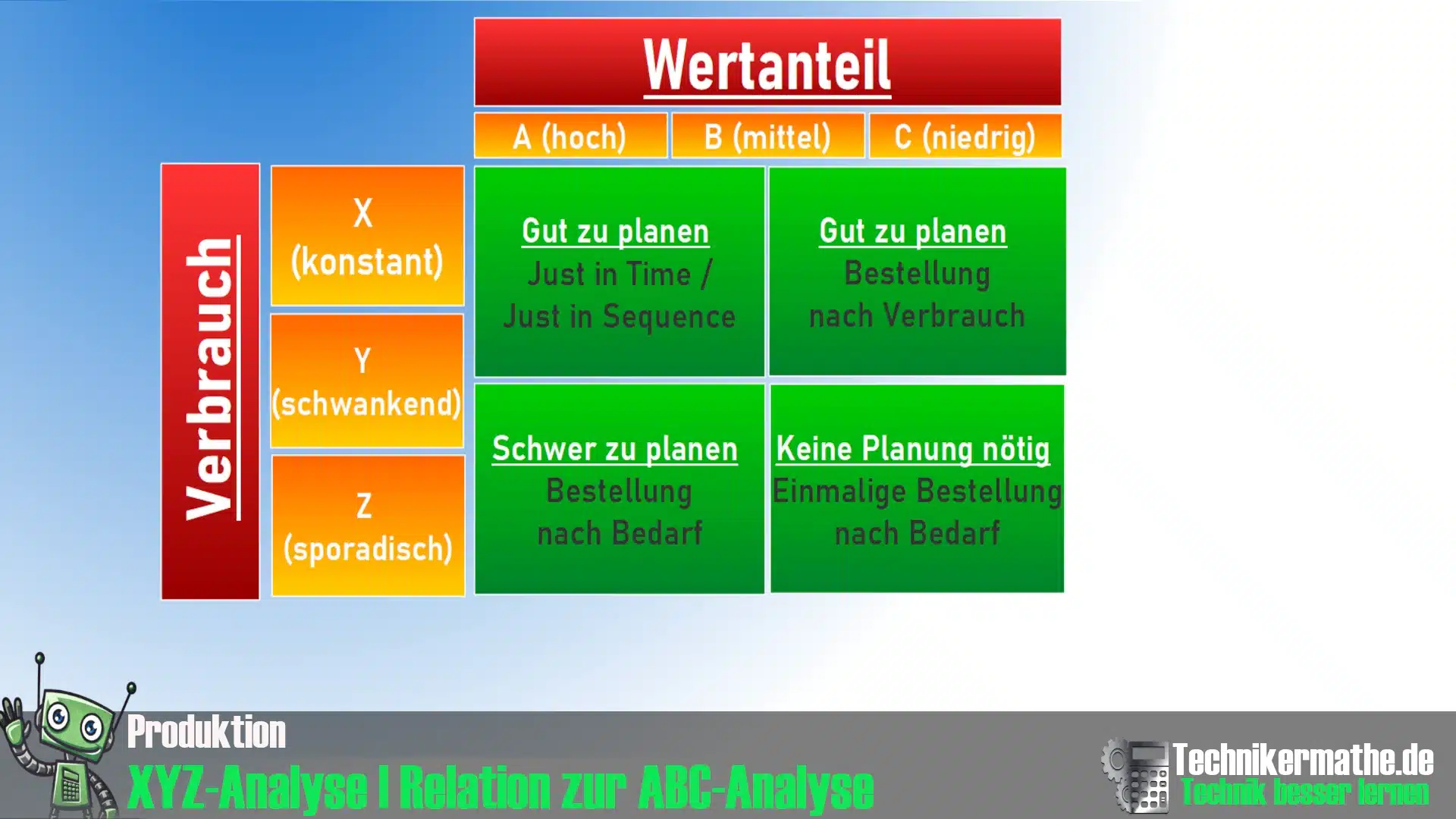
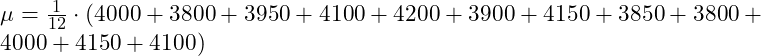PR2 – XYZ-Analyse [Definition, Beispiele, Berechnungen, Aufgaben]

Die XYZ-Analyse ist eine bedeutende Methode zur Bestands- und Materialplanung in der Produktion. Sie wird häufig in Kombination mit der ABC-Analyse verwendet, um sowohl den Verbrauch als auch die Schwankungen in der Nachfrage von Materialien oder Produkten zu bewerten. Während die ABC-Analyse den Fokus auf den Wert der Produkte legt, bewertet die XYZ-Analyse die Konstanz des Verbrauchs oder der Nachfrage.

XYZ-Analyse | RSU-Analyse [Verbrauchsverlaufsanalyse]

Was ist die XYZ-Analyse?

Definition

XYZ-Analyse?

Während die ABC-Analyse die Artikel nach ihrer finanziellen Bedeutung ordnet, klassifiziert die XYZ-Analyse die Materialien basierend auf ihrer Verlässlichkeit oder Vorhersagbarkeit des Bedarfs [Verbrauchsverhalten]. Die drei Kategorien in der Analyse sind X, Y und Z.

Übersicht der Kategorien der Verbrauchsverlaufanalyse

Hier ist eine Erläuterung der Kategorien:

X-Kategorie [alternativ: R] (Hoher Vorhersagbarkeitsgrad):

Materialien in der X-Kategorie sind sehr gut vorhersagbar. Die Nachfrage nach diesen Materialien kann mit hoher Genauigkeit prognostiziert werden. Diese Materialien haben einen stabilen und konsistenten Verbrauch. Die Bestände können effizient verwaltet werden, da die Bedarfsprognosen zuverlässig sind.

Beispiel: Standardprodukte mit konstantem Verbrauch, bei denen saisonale Schwankungen minimal sind.

Y-Kategorie [S] (Moderater Vorhersagbarkeitsgrad):

Materialien in der Y-Kategorie haben einen moderaten Grad an Vorhersagbarkeit. Die Nachfrage nach diesen Materialien kann schwanken, ist aber im Allgemeinen noch vorhersagbar. Die Bestandsverwaltung erfordert mehr Aufmerksamkeit als bei X-Kategoriematerialien, aber weniger als bei Z-Kategoriematerialien.

Beispiel: Produkte mit gelegentlichen Schwankungen in der Nachfrage, die jedoch insgesamt vorhersehbar sind.

Z-Kategorie [U] (Geringer Vorhersagbarkeitsgrad):

Materialien in der Z-Kategorie haben einen geringen Grad an Vorhersagbarkeit. Die Nachfrage nach diesen Materialien ist schwer vorhersehbar und kann unregelmäßig sein. Die Bestandsverwaltung erfordert intensive Überwachung und möglicherweise größere Sicherheitsbestände, um Engpässe zu vermeiden.

Beispiel: Saisonale oder trendige Produkte mit unregelmäßiger Nachfrage, die schwer vorhersehbar ist.

Klassifizierung:

Die XYZ-Kategorien können auf ähnliche Weise wie ABC in Prozentsätzen oder Mengen unterteilt werden. Typischerweise könnten die Top 20 % der Materialien als X, die nächsten 30 % als Y und die letzten 50 % als Z klassifiziert werden.

Die XYZ-Analyse unterstützt Unternehmen dabei, unterschiedliche Strategien für die Verwaltung ihrer Materialien zu entwickeln, je nach dem Grad der Vorhersagbarkeit der Nachfrage.

Bedeutung der XYZ-Analyse in der Produktion

Die XYZ-Analyse ist ein essenzielles Instrument, um eine präzise Bestandsplanung und Materialsteuerung zu gewährleisten. Sie hilft, den Lagerbestand basierend auf der Verbrauchskonstanz zu optimieren, und ermöglicht es Unternehmen, Engpässe zu vermeiden und die Verfügbarkeit kritischer Güter sicherzustellen.

Merk’s dir!

Mit der XYZ-Analyse lassen sich:

Bestellzyklen und Produktionsplanung besser an den tatsächlichen Bedarf anpassen.
Sicherheitsbestände für unregelmäßige Güter (Z-Güter) festlegen.
Lagerhaltungskosten durch gezielte Planung und Vorhersage des Bedarfs reduzieren.
Engpässe vermeiden, insbesondere bei schwer vorhersagbaren Produkten.

Variationskoeffizient

Die genaue Einteilung erfolgt rechnerisch mit dem Variationskoeffizient $Var_K$ . Der Variationskoeffizient (auch als relative Standardabweichung bezeichnet) ist ein statistisches Maß für die Streuung oder die relative Streuung einer Verteilung im Verhältnis zum Mittelwert.

Dieser Koeffizient gibt uns Auskunft darüber, in welchem Ausmaß ein Produkt im direkten Vergleich zu anderen Produkten von ungeplanten, unregelmäßigen Schwankungen betroffen ist.
Ein hoher Koeffizient zeugt im Vergleich zu einem geringer Koeffizient von einem starken unregelmäßigen Bedarf.

Formel

Der Variationskoeffizient wird oft in Prozent ausgedrückt.

Variationskoeffizient

$\text{Variationskoeffizient } = \frac{\text{Standardabweichung}}{\text{Mittelwert}} \cdot 100$

$\text{Var}_K = \frac{\sqrt{\sigma}}{\mu} \cdot 100$

mit

$Var_K =$ Variationskoeffizient in %
$\sigma =$ Standardabweichung
$\mu =$ Mittelwert

In der Fachliteratur spricht mal bei $\mu$ nicht selten von einem Erfahrungswert anstelle von einem Mittelwert. Beide stehen aber für die gleiche Aussage.

Schrittweise Berechnung des Variationskoeffizienten

Die Schritte zur Berechnung des Variationskoeffizienten sind:

Berechne den Mittelwert der Daten.
Berechne die Standardabweichung der Daten.
Teile die Standardabweichung durch den Mittelwert.
Multipliziere das Ergebnis mit 100, um den Variationskoeffizienten in Prozent auszudrücken.

Die Formel soll sicherstellen, dass der Variationskoeffizient unabhängig von den Einheiten der Daten ist, was es ermöglicht, die relative Streuung zwischen verschiedenen Datensätzen zu vergleichen, selbst wenn die Skalen unterschiedlich sind. Ein niedriger Variationskoeffizient deutet auf eine geringe relative Streuung hin, während ein hoher Koeffizient auf eine höhere Streuung im Verhältnis zum Mittelwert hinweist.

Beispiel zur Anwendung der XYZ-Analyse

Beispiel!

Wir betrachten erneut das Unternehmen aus dem Kursabschnitt ABC-Analyse.

Das Unternehmen hat nach der Konsultation eines externen Beraters entschieden, seine Materialwirtschaft zu überdenken. Es möchte die nachfolgenden Verbrauchspositionen in der Tabelle hinsichtlich ihres Bedarfsverhaltens überprüfen. Der betrachtete Zeitraum entspricht einem Kalenderjahr (Januar – Dezember).

Verbrauch der Teile (Produktionsfaktoren)
Kalendermonat	Spezialschrauben (1) [ $x_1$ ]	Scharniere (2) [ $x_2$ ]	Maschinenersatzteile (3) [ $x_3$ ]	Folie [Verpackung] (4) [ $x_4$ ]
Januar (2023)	4000	700	0	6000
Februar (2023)	3800	650	300	5500
März (2023)	3950	300	100	6000
April (2023)	4100	150	0	6500
Mai (2023)	4200	50	0	7000
Juni (2023)	3900	0	0	6000
Juli (2023)	4150	0	500	6800
August (2023)	3850	50	0	6000
September (2023)	3800	100	50	5700
Oktober (2023)	4000	150	0	6000
November (2023)	4150	300	0	6300
Dezember (2023)	4100	450	250	6200
Aufsummiert:	48000	2900	1200	74000

Lösung der Aufgabe

Im ersten Schritt errechnen wir für jede Verbrauchsposition

den Erwartungswert $\mu$ und
die Standardabweichung $\sigma$

Formal sieht das wie folgt aus:

$\mu = \frac{1}{12} \sum_{i = 1}^{12} x_i$

$\sigma = \sqrt{\frac{1}{12} \sum_{i = 1}^{12} (x_i - \mu)^2}$

Hier die Berechnung für den Erwartungswert $\mu$ der Spezialschrauben [Exemplarisches Beispiel]

$\mu = \frac{1}{12} \cdot (4000 + 3800 + 3950 + 4100 + 4200 + 3900 + 4150 + 3850 + 3800 + 4000 + 4150 + 4100)$

$\mu = \frac{1}{12} \cdot (48000)$

$\mu = 4000$

Die aufgerundeten Ergebnisse fassen wir in der nächsten Tabelle zusammen:

Produktionsfaktoren	Erwartungswert $\mu$	Standardabweichung $\sigma$
Spezialschrauben (1)	4000	135,4
Scharniere (2)	242	233,48
Maschinenersatzteile (3)	100	156,78
Folie [Verpackung] (4)	6167	410,96

Hier die Berechnung für den Standardabweichung $\sigma$ der Spezialschrauben [Exemplarisches Beispiel]

$\sigma = \sqrt{\frac{1}{12} \sum_{i = 1}^{12} (x_i - \mu)^2}$

$\sigma = \sqrt{\frac{1}{12} \cdot ((4000 - 4000)^2 + (3800 - 4000)^2 + (3950 - 4000)^2 + (4100 - 4000)^2 + (4200 - 4000)^2 + (3900 - 4000)^2}$

$\sqrt{+ (4150 - 4000)^2 + (3850 - 4000)^2 + (3800 - 4000)^2 + (4000 - 4000)^2 + (4150 - 4000)^2 + (4100 - 4000)^2)}$

$\sigma = \sqrt{\frac{1}{12} \cdot ((0)^2 + (-200)^2 + (-50)^2 + (100)^2 + (200)^2 + (-100)^2 + (150)^2 + (-150)^2 + (-200)^2 + (0)^2 + (150)^2 + (100)^2)}$

$\sigma = \sqrt{\frac{1}{12} \cdot (0 + 40000 + 2500 + 10000 + 40000 + 10000 + 22500 + 22500 + 40000 + 0 + 22500 + 10000}$

$\sigma = \sqrt{\frac{1}{12} \cdot (220000)}$

$\sigma = \sqrt{\frac{220000}{12}}$

$\sigma = \sqrt{18333,33}$

$\sigma = 135,40$

Im nächsten Schritt berechnen wir den Variationskoeffizient mit Hilfe der Ergebnisse aus der Tabelle:

$Var_K = (\frac{\sqrt{\sigma}}{\mu}) \cdot 100$

Hier die Berechnung für den Variationskoeffizienten der Spezialschrauben [Exemplarisches Beispiel]
$Var_K = (\frac{135,4}{4000}) \cdot 100$

$Var_K = (0,03385) \cdot 100 \approx 3,385 %$

Die Ergebnisse übertragen wir erneut in die Tabelle:

Produktionsfaktoren	Variationskoeffizient
Spezialschrauben (1)	3,39%
Scharniere (2)	96,45%
Maschinenersatzteile (3)	156,78%
Folie [Verpackung] (4)	6,67%

Die Festlegung der Klassengrenzen zur Zuordnung der individuellen Verbrauchsposten zu X-, Y- oder Z-Klassen variiert je nach Unternehmen. In diesem Fall werden die Klassengrenzen wie nachstehend definiert:

Klasse	Variationskoeffizient
X-Position	0 – 50 %
Y-Position	50 – 110 %
Z-Position	Ab 110 %

Im letzten Schritt ordnen wir die Produktionsfaktoren den Klassen zu:

Klasse	Produktionsfaktoren
X-Position	Spezialschrauben (1), Folie [Verpackung] (4)
Y-Position	Scharniere (2)
Z-Position	Maschinenersatzteile (3)

Die Bedarfe an Spezialschrauben und Folie zeigen nur geringe bis keine Schwankungen und sind daher gut vorhersehbar. Hier lässt sich beispielsweise durch die Einführung eines regelmäßigen Bestellrhythmus eine effiziente Kontrolle der Lagerhaltungskosten erreichen.
Im Gegensatz dazu unterliegt der Bedarf an Scharnieren erheblichen Schwankungen.
Die Maschinenersatzteile unterliegen einem äußerst unregelmäßigen Bedarf, was eine Planung kaum möglich macht.
In diesem Fall wird empfohlen, die Ersatzteile auf Lager zu halten, um jederzeit verfügbar zu sein. [/intense_content_box]

Vorteile der XYZ-Analyse

Bessere Vorhersagbarkeit: X-Güter lassen sich mit hoher Genauigkeit planen, was zu einer effizienteren Produktion und niedrigeren Lagerkosten führt.
Gezielte Bestandsplanung: Für Y- und Z-Güter kann durch höhere Sicherheitsbestände eine stärkere Absicherung erfolgen, um Engpässe zu vermeiden.
Ressourcenschonung: Unnötig hohe Lagerbestände für X-Güter können reduziert werden, da deren Verbrauch genau vorhersehbar ist.

Optimierung der XYZ-Analyse in der Produktion

Integration in ERP-Systeme: Moderne ERP-Systeme bieten automatisierte XYZ-Analyse-Module, die auf Echtzeitdaten basieren. Dies erleichtert die Analyse und hilft dabei, Änderungen im Verbrauchsmuster sofort zu erkennen.
Kombination mit der ABC-Analyse: Durch die Kombination der XYZ-Analyse mit der ABC-Analyse entsteht ein ganzheitlicher Ansatz. Zum Beispiel sind A-X-Güter sowohl wertvoll als auch konstant im Verbrauch, weshalb sie besonders sorgfältig verwaltet werden sollten.
Regelmäßige Aktualisierung: Wie bei der ABC-Analyse sollten auch die XYZ-Daten regelmäßig überprüft und aktualisiert werden, um den sich ändernden Marktbedingungen Rechnung zu tragen.

Herausforderungen der XYZ-Analyse

Unvorhersehbare Schwankungen: Z-Güter stellen eine große Herausforderung dar, da deren Verbrauch schwer planbar ist und hohe Sicherheitsbestände erforderlich machen.
Kostenintensive Bestandsführung für Z-Güter: Unternehmen müssen hohe Lagerbestände für Z-Güter halten, um mögliche Engpässe zu verhindern, was Lagerkosten erhöht.
Unvorhergesehene externe Faktoren: Externe Einflüsse wie Wirtschaftskrisen oder Lieferschwierigkeiten können die Vorhersagbarkeit von Y- und Z-Gütern erschweren.

Anwendung der XYZ-Analyse in der Produktion

Bestandsmanagement: X-Güter mit konstantem Verbrauch können präzise geplant und gelagert werden, während Z-Güter mit hohen Sicherheitsbeständen verwaltet werden müssen.
Lieferkettenoptimierung: Unternehmen können die XYZ-Analyse nutzen, um Lieferkettenentscheidungen zu treffen und Lagerbestände entsprechend anzupassen.
Produktionseffizienz: In der Produktionsplanung hilft die XYZ-Analyse, Materialien und Produktionskapazitäten auf Basis der Nachfragevorhersagbarkeit zu priorisieren.
Nachschubplanung: Durch die genaue Vorhersagbarkeit des Verbrauchs von X-Gütern können Nachschubpläne effizienter gestaltet und Kosten gesenkt werden.

XYZ-Analyse vs. ABC-Analyse

Die XYZ-Analyse und ABC-Analyse werden oft gemeinsam angewendet. Während die ABC-Analyse die Artikel nach ihrem Wert klassifiziert, bewertet die XYZ-Analyse die Vorhersagbarkeit ihres Verbrauchs. Eine Kombination dieser beiden Analysen führt zu einem ganzheitlichen Ansatz zur Produktions- und Lagerplanung. So lassen sich beispielsweise die wertvollsten und konstantesten Güter (A-X-Güter) effizient verwalten.

XYZ-Analyse in Relation zur ABC-Analyse | Wechselwirkungen | Verbrauchverlaufsanalyse — XYZ-Analyse in Relation zur ABC-Analyse | Wechselwirkungen | Verbrauchsverlaufanalyse

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Wann sollte die XYZ-Analyse angewendet werden?

Die XYZ-Analyse sollte insbesondere dann eingesetzt werden, wenn der Verbrauch von Produkten stark variiert und eine präzise Bestandsplanung entscheidend ist.

2. Wie oft sollte die XYZ-Analyse durchgeführt werden?

Die XYZ-Analyse sollte regelmäßig durchgeführt und an aktuelle Verbrauchsdaten angepasst werden, um Änderungen im Verbrauchsverhalten zu berücksichtigen.

3. Kann die XYZ-Analyse allein verwendet werden?

Die XYZ-Analyse kann allein verwendet werden, wird jedoch häufig mit der ABC-Analyse kombiniert, um sowohl Wert als auch Verbrauchsschwankungen zu berücksichtigen.

4. Wie wird der Variationskoeffizient berechnet?

Der Variationskoeffizient wird berechnet, indem die Standardabweichung des Verbrauchs durch den Mittelwert des Verbrauchs geteilt wird. Er gibt die Schwankungsintensität an.

5. Welche Maßnahmen ergreift man für Z-Güter?

Für Z-Güter, deren Verbrauch stark schwankt, sollte ein hoher Sicherheitsbestand vorgehalten werden, um Engpässe zu vermeiden.

Zusammenfassung

Die XYZ-Analyse ist ein wertvolles Instrument zur Optimierung der Produktions- und Lagerplanung. Sie hilft Unternehmen, Güter basierend auf ihrem Verbrauch und ihren Schwankungen zu klassifizieren, um Lagerbestände zu optimieren und Engpässe zu verhindern. In Kombination mit der ABC-Analyse kann die XYZ-Analyse einen ganzheitlichen Ansatz zur Verwaltung der wichtigsten Güter und Materialien bieten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++