[PR2] Minimalkostenkombination | Definition, Beispiele, Besonderheiten

Die Minimalkostenkombination ist ein entscheidendes Konzept der Produktionsökonomie, das Unternehmen dabei unterstützt, ihre Produktionskosten auf ein Minimum zu reduzieren, während sie eine bestimmte Produktionsmenge erreichen. In diesem Kursabschnitt erfährst du, wie du die Minimalkostenkombination berechnest und anwendest, um in deinem Unternehmen maximale Effizienz zu erzielen. Durch den gezielten Einsatz dieser Kombination kannst du deine Produktionskosten optimieren und gleichzeitig deine Wettbewerbsfähigkeit steigern.

Was ist die Minimalkostenkombination?

Definition

Was ist die Minimalkostenkombination?…

Die Minimalkostenkombination bezeichnet die optimale Kombination von Produktionsfaktoren, bei der ein bestimmtes Produktionsziel zu den geringstmöglichen Kosten erreicht wird. Dabei werden verschiedene Produktionsfaktoren wie Arbeit, Kapital und Rohstoffe so eingesetzt, dass die Gesamtkosten minimiert werden, ohne die Produktion zu verringern.

Minimalkostenkombination | Übersicht Tangentialpunkte, Isoquanten

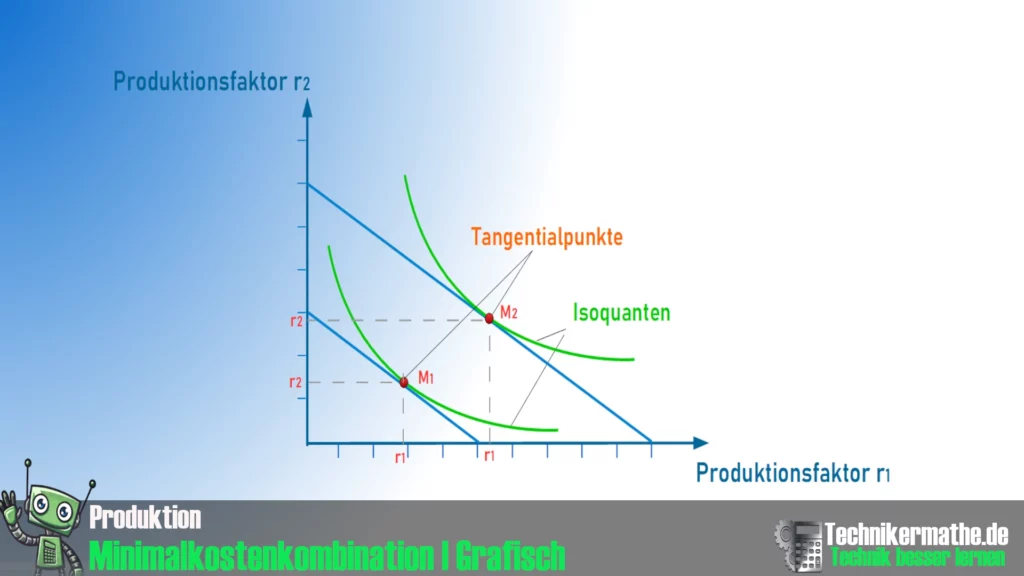
In der obigen Abbildung sind die roten Punkte, als jeweiliges Optimum gekennzeichnet.

Formel

Minimalkostenkombination

Mathematisch ausgedrückt bedeutet dies:

$\frac{MP_1}{P_1} = \frac{MP_2}{P_2} = …. = \frac{MP_n}{P_n}$

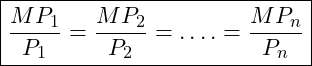
Dabei sind:

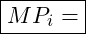$MP_i =$ Grenzprodukt des Faktors i
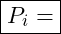$P_i =$ Preis des Faktors i

Kernelemente:

Optimale Faktorallokation:
- Die Produktionsfaktoren werden so kombiniert, dass die Kosten für die Produktion eines bestimmten Outputs minimal sind.
Grenzkostenbetrachtung:
- Es wird berücksichtigt, wie die Änderung der eingesetzten Menge eines Produktionsfaktors die Gesamtkosten beeinflusst, um die kostengünstigste Kombination zu ermitteln.
Effizienzsteigerung:
- Ziel ist es, die Effizienz in der Produktion zu maximieren, indem unnötige Kosten eliminiert werden.

Beispiel für eine Minimalkostenkombination

Beispiel!

Ein Unternehmen muss 1.000 Einheiten eines Produkts herstellen und hat die Wahl zwischen der Verwendung von mehr Arbeitskräften oder dem Einsatz von Maschinen. Die Minimalkostenkombination findet die kostengünstigste Kombination aus Arbeit und Maschinen, die diese Produktionsmenge sicherstellt.

Beispielaufgabe für eine Minimalkostenkombination

Aufgabenstellung

Angenommen ist die substitutionale Produktionsfunktion $x = \frac{1}{4} \sqrt{r_1} r_2$ , wobei die Faktorpreise $q_1 = 20$ und $q_2 = 16$ gegeben sind.

Gesucht ist die Faktorkombination, die zu minimalen Kosten führt.

Lösung

Zur Lösung leiten wir die Produktionsfunktion nach $r_1$ und $r_2$ ab:

$\frac{\partial x}{dr_1} = \frac{1}{4} \cdot 0,5 r_1^{-0,5} r_2$

$\frac{\partial x}{dr_2} = \frac{1}{4} r_1^{0,5}$

Setzen wir die Ableitungen in ein Verhältnis und setzen es mit den Faktorpreisen gleich:

$\frac{\frac{\partial x}{dr_1}}{\frac{\partial x}{dr_2}} = \frac{q_1}{q_2}$

$\frac{\frac{1}{4} \cdot 0,5 r_1^{-0,5} r_2}{\frac{1}{4} r_1^{0,5}} = \frac{20}{16}$

$\frac{0,5 r_2}{r_1} = \frac{20}{16}$

Durch Umformungen erhalten wir das Faktorverhältnis:

$\frac{r_2}{r_1} = 2,5 ; \rightarrow r_2 = 2,5r_1$

Das bedeutet, dass das optimale Faktorverhältnis $2,5 : 1$ beträgt oder anders ausgedrückt, $r_2$ ist das 2,5-fache von $r_1$ . Zum Beispiel, wenn $r_1$ mit 5 Einheiten in die Produktion einfließt, muss $r_2$ mit 12,5 Einheiten in die Produktion eingehen, um die Kosten zu minimieren.

Bedeutung der Minimalkostenkombination

Kostenreduktion und Gewinnsteigerung

Kostenoptimierung:
- Durch die Minimalkostenkombination können Unternehmen ihre Produktionskosten signifikant senken, was zu höheren Gewinnmargen führt.
Wettbewerbsvorteile:
- Unternehmen, die ihre Produktionsfaktoren optimal einsetzen, können Produkte zu wettbewerbsfähigeren Preisen anbieten und so Marktanteile gewinnen.
Ressourceneffizienz:
- Der effiziente Einsatz von Ressourcen trägt zur Schonung von Umweltressourcen bei und kann gleichzeitig Kosteneinsparungen fördern.

Vorteile für die Unternehmensstrategie

Flexibilität:
- Unternehmen können schnell auf Änderungen der Produktionsfaktorenpreise reagieren und ihre Produktionsprozesse entsprechend anpassen.
Langfristige Planung:
- Die Minimalkostenkombination hilft bei der Planung langfristiger Investitionen, indem sie die kosteneffizientesten Optionen identifiziert.
Risikomanagement:
- Durch die Optimierung der Produktionsfaktoren können Unternehmen Risiken besser managen, wie z.B. Preisschwankungen bei Rohstoffen.

Anwendung der Minimalkostenkombination in der Praxis

1. Bestimmung der Produktionsfaktoren

Um die Minimalkostenkombination zu berechnen, müssen zunächst alle verfügbaren Produktionsfaktoren identifiziert und ihre jeweiligen Kosten ermittelt werden.

Ziel:
- Die Faktoren identifizieren, die zur Herstellung des Produkts verwendet werden können.
Anwendung:
- Sammeln von Daten zu den Kosten aller relevanten Produktionsfaktoren (z.B. Lohnkosten, Materialkosten, Kapitalkosten).
Beispiel:
- Ein Produktionsunternehmen ermittelt die Kosten für Arbeitskräfte, Maschinenmiete und Rohstoffe, die für die Herstellung eines Produkts benötigt werden.

2. Kostenminimierung durch Faktorvariation

Unternehmen können durch die Variation und Kombination der Produktionsfaktoren die kosteneffizienteste Produktionsweise bestimmen.

Ziel:
- Die optimale Kombination von Produktionsfaktoren finden, die die geringsten Kosten verursacht.
Anwendung:
- Verwenden von Grenzkostenanalysen, um die Kostenänderungen bei Variation der Faktoreinsätze zu bewerten.
Beispiel:
- Durch den Vergleich der Kosten, die durch den Einsatz von mehr Maschinen oder mehr Arbeitskräften entstehen, ermittelt das Unternehmen die günstigste Produktionsmethode.

3. Langfristige Investitionsentscheidungen

Die Minimalkostenkombination kann auch als Grundlage für Investitionsentscheidungen verwendet werden, insbesondere wenn es um den Kauf von Anlagen oder Maschinen geht.

Ziel:
- Investitionen so planen, dass langfristig die Produktionskosten minimiert werden.
Anwendung:
- Bewertung der Amortisationszeiten von Investitionen und deren Einfluss auf die Produktionskosten.
Beispiel:
- Ein Unternehmen entscheidet sich für die Anschaffung neuer Maschinen, nachdem eine Analyse zeigt, dass dies langfristig die Gesamtkosten der Produktion senken wird.

Vorteile der Minimalkostenkombination

Effizienz und Kosteneinsparungen

Maximale Effizienz:
- Durch die Minimalkostenkombination wird sichergestellt, dass die Produktionsfaktoren optimal genutzt werden, was die Effizienz steigert.
Kostensenkung:
- Unternehmen können ihre Produktionskosten auf ein Minimum reduzieren, was direkt zu höheren Gewinnen führt.
Nachhaltige Produktion:
- Die effiziente Nutzung von Ressourcen fördert auch nachhaltige Produktionsmethoden.

Wettbewerbsvorteile und Marktvorteile

Preisvorteil:
- Unternehmen können durch niedrigere Produktionskosten ihre Produkte zu wettbewerbsfähigen Preisen anbieten.
Anpassungsfähigkeit:
- Die Flexibilität in der Kombination von Produktionsfaktoren ermöglicht es Unternehmen, schnell auf Marktveränderungen zu reagieren.
Investitionssicherheit:
- Unternehmen, die ihre Produktionsprozesse optimieren, können sicherer in neue Technologien oder Maschinen investieren, da die Kosten-Nutzen-Relation klar ist.

Herausforderungen und Lösungsansätze

Herausforderungen

Datenverfügbarkeit:
- Um die Minimalkostenkombination zu berechnen, sind umfassende und genaue Kostendaten erforderlich, die nicht immer leicht verfügbar sind.
Komplexität der Analyse:
- Die Analyse der optimalen Kombination von Produktionsfaktoren kann komplex und zeitaufwändig sein.
Dynamische Marktbedingungen:
- Preisschwankungen bei Produktionsfaktoren können die Optimierung erschweren.

Lösungsansätze

Einsatz moderner Analysetools:
- Moderne Softwarelösungen können bei der Sammlung und Analyse von Kostendaten unterstützen.
Schrittweise Implementierung:
- Unternehmen können die Minimalkostenkombination schrittweise einführen, um Risiken zu minimieren und Anpassungen vorzunehmen.
Regelmäßiges Monitoring:
- Kontinuierliches Monitoring der Produktionskosten und -faktoren hilft, die Optimierung anzupassen und auf Veränderungen zu reagieren.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Minimalkostenkombination?

Sie bezeichnet die optimale Kombination von Produktionsfaktoren, bei der ein Produktionsziel zu den geringstmöglichen Kosten erreicht wird.

2. Wie kann ich die Minimalkostenkombination in meinem Unternehmen berechnen?

Indem Sie die Kosten aller relevanten Produktionsfaktoren erfassen und dann die Kombination wählen, die die geringsten Gesamtkosten verursacht.

3. Welche Vorteile bietet die Minimalkostenkombination?

Sie ermöglicht signifikante Kosteneinsparungen, erhöht die Effizienz und verbessert die Wettbewerbsfähigkeit Ihres Unternehmens.

4. Kann die Minimalkostenkombination auch bei kleinen Unternehmen angewendet werden?

Ja, auch kleine Unternehmen können von der Anwendung der Minimalkostenkombination profitieren, da sie hilft, die Produktionskosten zu senken und Ressourcen effizient zu nutzen.

5. Welche Rolle spielt die Minimalkostenkombination bei Investitionsentscheidungen?

Sie hilft Unternehmen, Investitionen in neue Technologien oder Produktionsmethoden zu planen, indem sie die kosteneffizienteste Option identifiziert.

Zusammenfassung

Die Minimalkostenkombination ist ein leistungsstarkes Werkzeug, das Unternehmen dabei unterstützt, ihre Produktionskosten zu optimieren und ihre Effizienz zu maximieren. Durch die sorgfältige Analyse und Kombination von Produktionsfaktoren können Unternehmen ihre Wettbewerbsfähigkeit steigern und langfristige Kostenvorteile erzielen. Die Anwendung dieses Konzepts erfordert zwar eine gründliche Datenerhebung und Analyse, bietet jedoch erhebliche Vorteile in Form von Kosteneinsparungen, Effizienzsteigerungen und verbesserten Investitionsentscheidungen. Unternehmen, die die Minimalkostenkombination effektiv nutzen, sind in der Lage, ihre Produktionsprozesse kontinuierlich zu verbessern und ihre Position auf dem Markt zu stärken.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++