Die linear-limitationale Kostenfunktion ist ein zentrales Konzept in der Produktionswirtschaft, das Unternehmen hilft, ihre Kostenstrukturen zu verstehen und zu optimieren. In diesem Kursabschnitt erfährst du, wie diese Kostenfunktion funktioniert, wie sie angewendet wird und welche Vorteile sie für die Produktionsplanung bietet.

Was ist die linear-limitationale Kostenfunktion?
Definition
Die linear-limitationale Kostenfunktion beschreibt die Beziehung zwischen der Produktionsmenge und den dabei entstehenden Kosten, unter der Annahme, dass die Produktionsfaktoren in festen Proportionen eingesetzt werden. Diese Art von Kostenfunktion ist linear, was bedeutet, dass die Kosten direkt proportional zur Produktionsmenge steigen, solange die Kapazitätsgrenzen der Produktionsfaktoren nicht überschritten werden.
Alternative Bezeichnungen für die linear-limitationale Kostenfunktion sind:
- Proportionale Kostenfunktion
- Lineare Kostenfunktion
- Additive Kostenfunktion
Alle diese Begriffe drücken aus, dass die Kosten in einem festen Verhältnis zur Produktionsmenge stehen und sich aus der Summe der proportionalen Kosten der einzelnen Produktionsfaktoren ergeben.
Formel
![]()
Kennzahlen
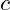 die Fixkosten,
die Fixkosten, die variablen Kosten pro Einheit des Faktors
die variablen Kosten pro Einheit des Faktors 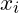 , und
, und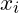 die Menge des Faktors i
die Menge des Faktors i
Diese Funktion ist limitational, da die variablen Kosten pro Einheit konstant sind. Die linear-limitatonale Kostenfunktion besitzt bereits eine vorgegeben Faktormengenkombination.
Grafische Darstellung

Das Konzept linear-limitational beschreibt eine Beziehung zwischen zwei Produktionsfaktoren [Hier r1 und r2], bei der diese in einem festen Verhältnis zueinander eingesetzt werden müssen, um eine bestimmte Outputmenge [hier x] zu produzieren. Das bedeutet, dass die Produktionsfaktoren nicht gegeneinander substituiert werden können. Wenn beispielsweise ein Produktionsprozess genau 2 Maschinenstunden und 3 Arbeitsstunden für die Herstellung eines Produkts erfordert, kann das Verhältnis nicht verändert werden, ohne die Produktion zu beeinträchtigen. Diese Art der Produktionsfunktion ist durch eine lineare Beziehung gekennzeichnet, bei der die Inputmengen direkt proportional zum Output steigen.

In der obigen Abbildung wird deutlich, dass die Erhöhung eines einzigen Produktionsfaktors [![]() oder
oder ![]() ] nicht zu einer Erhöhung der Produktionsmenge | Ausbringung [
] nicht zu einer Erhöhung der Produktionsmenge | Ausbringung [![]() ] führt. Siehe hierzu die roten gestrichelten Linien.
] führt. Siehe hierzu die roten gestrichelten Linien.
In unserer derzeitigen Überlegung gehen wir immer von zwei Produktionsfaktoren aus. Bei drei oder mehr Produktionsfaktoren gestaltet sich die grafische Darstellung wesentlich komplexer.
Kernelemente:
-
Linearität:
- Die Kosten steigen linear mit der Produktionsmenge, ohne dass Skaleneffekte auftreten.
-
Limitationalität:
- Produktionsfaktoren müssen in festen Proportionen kombiniert werden, z.B. eine bestimmte Menge Arbeitskraft pro Maschine.
-
Proportionalität:
- Kosten ändern sich proportional zur Veränderung der Produktionsmenge.
Beispiel für eine linear-limitationale Kostenfunktion
Angenommen, ein Unternehmen stellt ein Produkt her, bei dem für jede produzierte Einheit genau eine Arbeitskraft und eine Maschine benötigt werden. Die Kosten für die Arbeitskraft und die Maschine steigen proportional zur Produktionsmenge.
Bedeutung der linear-limitationale Kostenfunktion
Transparenz und Planbarkeit
-
Einfache Kostenprognose:
- Da die Kosten linear steigen, lassen sich zukünftige Kosten bei Produktionsänderungen leicht prognostizieren.
-
Klare Kostenstrukturen:
- Unternehmen können die Kosten für einzelne Produktionsschritte leicht nachvollziehen und optimieren.
-
Kalkulierbare Entscheidungen:
- Entscheidungen über Produktionsausweitungen oder -kürzungen können auf Basis klarer Kostenprognosen getroffen werden.
Vorteile für die Produktionsplanung
-
Effiziente Ressourcennutzung:
- Da die Kostenfunktion limitational ist, wird eine Übernutzung von Produktionsfaktoren vermieden.
-
Einfache Budgetierung:
- Unternehmen können ihre Budgets präzise planen, da die Kostensteigerungen linear und vorhersehbar sind.
-
Optimierungspotenzial:
- Identifikation von Kostensenkungspotenzialen durch Analyse der Kostenstruktur und Effizienzsteigerung.
Anwendung der linear-limitationale Kostenfunktion in der Praxis
1. Kostenkalkulation
Unternehmen nutzen die linear-limitationale Kostenfunktion, um die Gesamtkosten ihrer Produktion zu kalkulieren.
-
Ziel:
- Ermittlung der Gesamtkosten für verschiedene Produktionsmengen.
-
Anwendung:
- Aufstellen einer linearen Gleichung, die die Gesamtkosten in Abhängigkeit von der Produktionsmenge beschreibt (z.B. Gesamtkosten = Fixkosten + variable Kosten pro Einheit * Produktionsmenge).
-
Beispiel:
- Ein Unternehmen produziert 1.000 Einheiten eines Produkts. Die Fixkosten betragen 10.000 Euro, die variablen Kosten pro Einheit 50 Euro. Die Gesamtkosten sind: 10.000 Euro + 50 Euro * 1.000 Einheiten = 60.000 Euro.
2. Kapazitätsplanung
Die linear-limitationale Kostenfunktion hilft, die Kapazitätsauslastung optimal zu planen und Engpässe zu vermeiden.
-
Ziel:
- Sicherstellung einer effizienten Nutzung von Produktionsfaktoren ohne Überschreitung der Kapazitätsgrenzen.
-
Anwendung:
- Analyse der Kapazitätsauslastung, um die Produktionsmenge so zu planen, dass die lineare Beziehung zwischen Kosten und Produktion erhalten bleibt.
-
Beispiel:
- Ein Unternehmen hat eine maximale Maschinenkapazität von 2.000 Einheiten pro Monat. Wird diese Grenze überschritten, steigen die Kosten überproportional.
3. Break-even-Analyse
Mit der linear-limitationale Kostenfunktion können Unternehmen den Break-even-Punkt, also den Punkt, an dem die Kosten durch die Erlöse gedeckt werden, leicht berechnen.
-
Ziel:
- Bestimmung der minimalen Produktionsmenge, bei der das Unternehmen profitabel arbeitet.
-
Anwendung:
- Berechnung des Break-even-Punkts durch Setzen der Gesamtkosten gleich den Gesamterlösen.
-
Beispiel:
- Bei einem Verkaufspreis von 100 Euro pro Einheit und variablen Kosten von 50 Euro pro Einheit beträgt die Break-even-Menge: Fixkosten / (Verkaufspreis – variable Kosten).
Vorteile der linear-limitationale Kostenfunktion
Einfache Implementierung
-
Leichte Berechnung:
- Die lineare Struktur der Kostenfunktion macht die Berechnung und Analyse der Kosten einfach und intuitiv.
-
Klare Entscheidungsgrundlage:
- Die Vorhersehbarkeit der Kostenentwicklung bietet eine sichere Basis für Investitionsentscheidungen.
-
Geringer Planungsaufwand:
- Durch die Einfachheit der Funktion wird der Planungsaufwand minimiert.
Flexibilität und Anpassungsfähigkeit
-
Anpassung an Produktionsänderungen:
- Die lineare Kostenfunktion ermöglicht eine schnelle Anpassung an Veränderungen der Produktionsmengen.
-
Kosteneffiziente Produktion:
- Die Proportionalität der Kosten bietet Anreize für eine effiziente Produktionsplanung.
-
Vermeidung von Ressourcenverschwendung:
- Die Limitationalität der Funktion sorgt dafür, dass Produktionsfaktoren optimal eingesetzt werden, ohne Verschwendung zu verursachen.
Herausforderungen und Lösungsansätze
Herausforderungen
-
Begrenzte Anwendbarkeit:
- Die linear-limitationale Kostenfunktion ist nur bei linearen Kostenverläufen und festen Faktorproportionen anwendbar.
-
Ignoriert Skaleneffekte:
- Mögliche Kostenvorteile durch Skaleneffekte werden nicht berücksichtigt.
Lösungsansätze
-
Kombination mit anderen Kostenfunktionen:
- Bei nicht-linearen Kostenverläufen oder variablen Faktorproportionen sollten andere Kostenfunktionen oder hybride Ansätze verwendet werden.
-
Berücksichtigung von Skaleneffekten:
- Ergänzung der linearen Funktion durch Modelle, die Skaleneffekte berücksichtigen, um eine genauere Kostenanalyse zu ermöglichen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist die linear-limitationale Kostenfunktion?
- Eine Kostenfunktion, bei der die Kosten proportional zur Produktionsmenge steigen und Produktionsfaktoren in festen Proportionen kombiniert werden.
2. Wie unterscheidet sich die linear-limitationale Kostenfunktion von anderen Kostenfunktionen?
- Sie unterscheidet sich durch ihre lineare Struktur und die Annahme fester Proportionen bei den Produktionsfaktoren, was sie besonders einfach zu berechnen und zu interpretieren macht.
3. Welche Vorteile bietet die linear-limitationale Kostenfunktion?
- Sie ermöglicht eine einfache und transparente Kostenkalkulation, eine effiziente Kapazitätsplanung und eine klare Entscheidungsgrundlage für die Produktionsplanung.
4. In welchen Situationen ist die linear-limitationale Kostenfunktion besonders nützlich?
- Sie ist besonders nützlich, wenn die Produktionskosten linear zur Produktionsmenge steigen und die Produktionsfaktoren in festen Proportionen eingesetzt werden.
5. Wie kann die linear-limitationale Kostenfunktion in der Praxis angewendet werden?
- Sie kann zur Kostenkalkulation, Kapazitätsplanung und Break-even-Analyse eingesetzt werden, um Produktionsprozesse effizient zu gestalten und Kosten zu minimieren.
Zusammenfassung
Die linear-limitationale Kostenfunktion ist ein wertvolles Werkzeug für die Produktionsplanung, das Unternehmen eine einfache und transparente Kostenkalkulation ermöglicht. Durch ihre lineare Struktur und die feste Proportion der Produktionsfaktoren bietet sie eine klare Entscheidungsgrundlage für die Optimierung der Produktionsprozesse. Trotz ihrer begrenzten Anwendbarkeit in komplexeren Produktionsumgebungen bleibt sie eine effektive Methode zur Kostenkontrolle und Effizienzsteigerung in der Produktion. Unternehmen, die die linear-limitationale Kostenfunktion nutzen, können ihre Produktionskosten effektiv steuern und langfristig Wettbewerbsvorteile erzielen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






