Die Limitationalität ist ein grundlegender Begriff der Produktions- und Wirtschaftstheorie, der sich auf Situationen bezieht, in denen Produktionsfaktoren nur in einem festen Verhältnis kombiniert werden können, um eine bestimmte Menge an Output zu erzielen. Anders als bei der Substitutionalität fehlt hier die Flexibilität, einen Faktor durch einen anderen zu ersetzen.
Was ist die Limitationalität?
Definition
Die Limitationalität beschreibt ein starres Verhältnis zwischen den Produktionsfaktoren, bei dem jeder Faktor nur in einer bestimmten Kombination mit anderen Faktoren genutzt werden kann, um Output zu erzeugen. Ein Abweichen von diesem festen Verhältnis führt zu ineffizienter oder gar unmöglicher Produktion.
Beispielsweise kann in einem Produktionsprozess menschliche Arbeitskraft (Inputfaktor 1) durch Maschinen (Inputfaktor 2) ersetzt werden, solange die Effizienz des Outputs konstant bleibt. Diese Eigenschaft ermöglicht eine flexible Ressourcenallokation.
Dies wird in der folgenden Grafik verdeutlicht. Dem Faktoraustausch werden Grenzen (Limits!) gesetzt.
Jetzt sind keine Isoquanten als Produktionsfunktion vorhanden, sondern lediglich Punkte (blau), in denen die Produktionsfunktion erfüllt ist.
Wichtige Informationen zur Limitationalität
-
Faktorproportionen: Die Produktion erfordert ein fixes Verhältnis der Faktoren. Bei Abweichungen ist der Output limitiert.
Beispiel: Für die Montage eines Stuhls benötigt man exakt 4 Schrauben und 1 Sitzfläche. Fehlen Schrauben oder Sitzflächen, kann der Stuhl nicht vollständig hergestellt werden. -
Keine Substitutionsmöglichkeit: Ein Faktor kann nicht durch einen anderen ersetzt werden. Es gibt keine Flexibilität in der Kombination der Produktionsfaktoren.
-
Begrenzender Faktor (Engpassfaktor): Der Faktor, dessen Menge zuerst ausgeschöpft ist, bestimmt die Produktionsgrenze.
Beispiel: In einer Bäckerei, in der Mehl knapp ist, begrenzt die verfügbare Mehlmenge die Anzahl der produzierbaren Brötchen. -
Lineare Skalierbarkeit: Wenn die Inputfaktoren proportional erhöht werden, steigt der Output linear.
-
Bezug zu Leontief-Produktionsfunktionen: Limitationale Produktionsfunktionen werden oft durch Leontief-Produktionsfunktionen modelliert, die feste Faktorverhältnisse voraussetzen.
Anschauliche Beispiele für Limitationalität
1. Kuchen backen
Beim Backen eines Kuchens gibt es ein festgelegtes Rezept mit genauen Mengenangaben für Mehl, Zucker, Butter und Eier. Werden diese Proportionen nicht eingehalten, ist das Ergebnis kein genießbarer Kuchen. Beispielsweise führt das Verdoppeln des Mehls ohne Anpassung der anderen Zutaten zu einem unbrauchbaren Teig.
2. Autoproduktion
In einer Automobilfabrik erfordert die Fertigung eines Autos eine feste Menge an Karosserieteilen, Reifen, Motoren und Elektronik. Wenn ein Teil fehlt (z. B. die Reifen), kann das Fahrzeug nicht fertiggestellt werden.
3. Stromproduktion
In einem Kohlekraftwerk ist für die Stromproduktion eine bestimmte Menge Kohle und Sauerstoff erforderlich. Fehlt einer der beiden Faktoren, bricht der Produktionsprozess ab.
4. Teamarbeit
Ein Bauprojekt benötigt ein festes Team aus Architekten, Bauingenieuren und Arbeitern. Fehlt eine der Gruppen, kann das Projekt nicht abgeschlossen werden.
5. Landwirtschaft
Der Ertrag auf einem Feld hängt von der optimalen Kombination von Wasser, Dünger und Samen ab. Eine Überversorgung eines Faktors (z. B. Dünger) bringt keinen zusätzlichen Ertrag, wenn die anderen Faktoren limitiert sind.
Beispiel
Ein einfaches Beispiel verdeutlicht dies: das Backen eines Kuchens. Wenn man beim Zubereiten des Teigs den Anteil des Mehls halbiert und gleichzeitig den des Salzes verdoppelt, würde man nach dem Backvorgang ein ungenießbaren Kuchen erhalten, nur weil das vorgegebene Mischverhältnis nicht beachtet wurde.
Um 10 Brötchen zu backen, benötigt der Bäcker die doppelte Menge an Faktoreinsätzen im Vergleich zur Produktion von 5 Brötchen. Das bedeutet, dass jeder Inputfaktor, sei es Mehl (r1), Wasser (r2), Hefe (r3) oder Salz (r4), verdoppelt wird. Mathematisch ausgedrückt ergibt sich dies durch den Multiplikator λ = 2:
Hierbei stehen 
für die Mengen der einzelnen Faktoren (Mehl, Wasser, Hefe, Salz) für die Produktion von 5 Brötchen, und x repräsentiert die Outputmenge von 10 Brötchen.
Grenzfälle und mathematische Darstellung
In der Limitationalität gibt es keine substituierbaren Faktoren. Wenn eine Produktionsfunktion wie folgt aussieht:
kann man folgende Szenarien ableiten:
- Für
und ergibt sich 
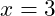. - Erhöht man
auf 8, bleibt der Output weiterhin bei 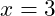, solange 
unverändert bleibt.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist der Unterschied zwischen Limitationalität und Substitutionalität?
- Bei der Limitationalität müssen Produktionsfaktoren in einem festen Verhältnis kombiniert werden.
- Bei der Substitutionalität können Faktoren flexibel ersetzt werden.
2. Warum ist Limitationalität in der Praxis wichtig?
Sie zeigt, dass der Output oft durch den knappsten Produktionsfaktor begrenzt wird (Engpassmanagement).
3. Welche Branchen sind von Limitationalität betroffen?
Praktisch alle Produktionsprozesse mit festen Rezepturen oder Standards, wie in der Lebensmittelindustrie, der Automobilproduktion und der Energiewirtschaft.
4. Gibt es Möglichkeiten, Limitationalität zu umgehen?
Ja, durch Innovationen und Prozessoptimierungen können neue Wege gefunden werden, Produktionsprozesse flexibler zu gestalten.
5. Was passiert, wenn ein Faktor knapp wird?
Der Output sinkt proportional zur Verfügbarkeit des limitierenden Faktors.
Zusammenfassung
Die Limitationalität beschreibt Produktionsprozesse, in denen ein festes Verhältnis zwischen den Produktionsfaktoren eingehalten werden muss. Dieses Konzept ist in vielen realen Szenarien relevant, von der Lebensmittelherstellung bis hin zur industriellen Fertigung. Anders als bei der Substitutionalität gibt es hier keine Flexibilität im Austausch der Faktoren. Die wichtigsten Punkte zusammengefasst:
- Feste Faktorproportionen sind notwendig.
- Ein limitierender Faktor (Engpassfaktor) bestimmt die maximale Produktionsmenge.
- Anschauliche Beispiele finden sich im Alltag (z. B. Kuchen backen) und in der Industrie (z. B. Autoproduktion).
- Limitationalität zeigt, dass Effizienz oft durch den knappsten Faktor begrenzt wird.
Mit diesem Wissen wird klar, wie wichtig ein Verständnis von limitationalen Prozessen für Unternehmen und Organisationen ist, um Engpässe zu vermeiden und die Produktion zu optimieren.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team
