Die Leontief-Produktionsfunktion ist eine spezielle Form der Produktionsfunktion, die lineare Beziehungen zwischen den Produktionsfaktoren darstellt.

Was ist die Leontief-Produktionsfunktion?
Definition
Die Leontief-Produktionsfunktion, benannt nach dem Ökonomen Wassily Leontief, beschreibt Produktionsprozesse, bei denen die Einsatzverhältnisse der Faktoren festgelegt sind. Diese Funktion geht davon aus, dass eine Substitution zwischen den Faktoren nicht möglich ist. Stattdessen wird die Produktionsmenge durch den knappsten Faktor, den sogenannten Engpassfaktor, begrenzt.
Schlüsselmerkmale
- Fixe Faktorverhältnisse: Kein Spielraum für Substitution.
- Engpassorientierung: Der knappste Faktor limitiert den Output.
- Effizienz im Einsatz: Alle Faktoren müssen in den optimalen Mengen vorliegen, um die maximale Produktionsmenge zu erreichen.
Formel
Die allgemeine Form der Leontief-Produktionsfunktion lässt sich wie folgt darstellen:
![]()
Bedeutung der Variablen:
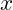 : Outputmenge (Produktionsmenge)
: Outputmenge (Produktionsmenge) : Einsatzmenge des Faktors
: Einsatzmenge des Faktors 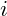
 : Feste Einsatzverhältnisse des Faktors
: Feste Einsatzverhältnisse des Faktors 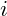
Der Output wird durch das Minimum der Verhältnisse der vorhandenen Faktorressourcen zu den notwendigen Einsatzverhältnissen bestimmt.
Dabei repräsentiert x die Outputmenge, ![]() sind die Mengen der verschiedenen Produktionsfaktoren, und
sind die Mengen der verschiedenen Produktionsfaktoren, und ![]() sind die fixen Faktoreneinsatzverhältnisse.
sind die fixen Faktoreneinsatzverhältnisse.
Die Leontief-Produktionsfunktion drückt aus, dass die Produktion durch den knappsten Faktor begrenzt wird, und es gibt keinen Spielraum für Substitution zwischen den Faktoren.
Die Berechnung des Outputs erfolgt durch das Minimum der Verhältnisse der Faktorenmengen zu den fixen Einsatzverhältnissen.
Beispiele
Angenommen, die Leontief-Produktionsfunktion lautet:
![]()
Wenn ![]() und
und ![]() sind, dann ist das Minimum min
sind, dann ist das Minimum min ![]() , was bedeutet, dass die Outputmenge aufgrund des knappsten Faktors (in diesem Fall
, was bedeutet, dass die Outputmenge aufgrund des knappsten Faktors (in diesem Fall ![]() ) auf 3 begrenzt ist.
) auf 3 begrenzt ist.
Wenn man die Leontief-Produktionsfunktion auf ein einzelnes Produktionsverfahren festlegt, lässt sie sich für die einstufige Produktion eines Produktes durch das folgende System von Faktorfunktionen darstellen:
![]()
![]()
…
![]()
mit ![]()
Hierbei sind ![]() konstante Produktionskoeffizienten. Die maximale Produktionsmenge lautet entsprechend:
konstante Produktionskoeffizienten. Die maximale Produktionsmenge lautet entsprechend:
![]()
mit ![]()
Greifen wir erneut das Beispiel mit den Brötchen auf:
Für die Produktion von 5 Brötchen (![]() ) benötigt man 400g Mehl (
) benötigt man 400g Mehl (![]() ), 200 ml Wasser (
), 200 ml Wasser (![]() ), 2 TL Salz (
), 2 TL Salz ( ![]() ) und 10 g Hefe (
) und 10 g Hefe (![]() ). Weitere Faktoreinsätze werden vernachlässigt.
). Weitere Faktoreinsätze werden vernachlässigt.
Die Faktorfunktionen für einen linear-limitationalen Fertigungsvorgang ergeben sich wie folgt:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Daraus lässt sich die maximale Produktionsmenge berechnen:
![]()
![]()
Diese Funktion repräsentiert die Produktionsfunktion mit effizientem Endprodukt. Anhand dieser kann nun der Output berechnet werden.
Angenommen, folgende Höchsteinsatzmengen für das obige Beispiel sind gegeben:
Höchsteinsatzmengen: 1200 g Mehl, 600 ml Wasser, 6 TL Salz, 20 g Hefe.
Zur Berechnung der maximalen Produktionsmenge benötigt man nun die obige Formel:
![]()
![]()
![]()
Es zeigt sich also, dass sich die Produktionsmenge nach dem Faktor richtet, welcher nach dem Input-Output Verhältnis am geringsten vorhanden ist.
Engpassfaktor
Dieser Faktor wird auch Engpassfaktor genannt. In diesem Beispiel könnten mit ![]() der Output verdreifacht werden (also 3x = 15 Brötchen hergestellt werden), allerdings ist die Hefe in diesem Beispiel der Engpassfaktor, der lediglich die Herstellung der doppelten Menge an Brötchen (also 2x = 10 Brötchen) zulässt.
der Output verdreifacht werden (also 3x = 15 Brötchen hergestellt werden), allerdings ist die Hefe in diesem Beispiel der Engpassfaktor, der lediglich die Herstellung der doppelten Menge an Brötchen (also 2x = 10 Brötchen) zulässt.
Erst wenn alle Einsatzfaktoren Engpassfaktoren darstellen, ist die effizienteste Kombination gefunden. In diesem Beispiel müsste die Hefe 30g betragen:
![]()
Erst jetzt sind die Faktoreinsätze effizient.
Isoquanten der Leontief-Produktionsfunktion
Die Isoquanten bei der Leontief-Produktionsfunktion haben eine ganz besondere Form, die ihre Eigenschaften gut verdeutlicht.
![Isoquanten der Leontief-Produktionsfunktion [L-Förmige Gestalt] Isoquanten der Leontief-Produktionsfunktion [L-Förmige Gestalt]](https://technikermathe.de/wp-content/uploads/2024/08/0031-Produktion-Leontief-Produktionsfunktion.webp)
Lass uns das genauer anschauen:
Definition der Isoquante
Eine Isoquante ist eine Linie, die alle Kombinationen von Inputs (z. B. Arbeit und Kapital) zeigt, mit denen dieselbe Produktionsmenge erreicht wird.
Bei der Leontief-Produktionsfunktion:
Die Inputs müssen in einem festen Verhältnis stehen, zum Beispiel:
![]()
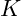 : Menge an Kapital
: Menge an Kapital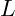 : Menge an Arbeit
: Menge an Arbeit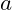 und
und 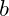 : feste Verhältnisse der Inputs
: feste Verhältnisse der Inputs
Form der Isoquanten:
- Rechteckig oder L-förmig:
- Der “Knick” der Isoquante [Siehe Bild oben] liegt genau dort, wo das Verhältnis
 erfüllt ist.
erfüllt ist. - Auf den senkrechten oder waagrechten Linien der Isoquante ändert sich die Produktionsmenge nicht, da der zusätzliche Input nicht genutzt werden kann.
- Der “Knick” der Isoquante [Siehe Bild oben] liegt genau dort, wo das Verhältnis
Beispiel:
Angenommen, ![]() (1 Einheit Kapital) und
(1 Einheit Kapital) und ![]() (2 Einheiten Arbeit) sind notwendig für 1 Einheit Output
(2 Einheiten Arbeit) sind notwendig für 1 Einheit Output ![]() .
.
Isoquante für ![]() :
:
Kapital = 1, Arbeit = 2 (![]() ) → “Knickpunkt” der Isoquante.
) → “Knickpunkt” der Isoquante.
Zusätzliche Arbeit (z. B. ![]() ) oder zusätzliches Kapital (z. B.
) oder zusätzliches Kapital (z. B. ![]() ) erhöhen
) erhöhen ![]() nicht.
nicht.
Isoquante für ![]() :
:
![]() (feste Verhältnisse verdoppelt).
(feste Verhältnisse verdoppelt).
Die Isoquanten sind also nicht glatt und abfallend wie bei anderen Produktionsfunktionen, sondern bestehen aus senkrechten und waagrechten Abschnitten mit einem Knick.
Interpretation:
- Auf der waagrechten Linie der Isoquante: Mehr Kapital bringt keinen zusätzlichen Output, da Arbeit limitiert ist.
- Auf der senkrechten Linie: Mehr Arbeit bringt keinen zusätzlichen Output, da Kapital limitiert ist.
So zeigen die Isoquanten der Leontief-Produktionsfunktion die strikten Mindestanforderungen für die Inputs, die eingehalten werden müssen.
Wichtige Informationen
- Engpassfaktor: Der Output hängt direkt vom knappsten Faktor ab.
- Keine Substitution: Faktoren können nicht durch andere ersetzt werden.
- Fixe Einsatzverhältnisse: Änderungen eines Faktors beeinflussen den Output nur dann, wenn andere Faktoren ebenfalls angepasst werden.
- Anwendungsgebiete: Die Funktion wird häufig in der linearen Programmierung und Input-Output-Analyse verwendet.
- Effizienz: Maximale Produktionsmengen werden nur erreicht, wenn alle Faktoren optimal kombiniert sind.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Warum ist die Leontief-Produktionsfunktion so wichtig?
Sie zeigt die Grenzen auf, die durch fixe Produktionsverhältnisse entstehen, und bietet eine Grundlage für Effizienzanalysen in der Produktion.
2. Was ist der Unterschied zwischen der Leontief- und der Cobb-Douglas-Produktionsfunktion?
Während die Leontief-Funktion keine Substitution zwischen Faktoren erlaubt, ermöglicht die Cobb-Douglas-Funktion eine flexible Anpassung der Faktoreinsatzmengen.
3. Wie wird der Engpassfaktor identifiziert?
Der Engpassfaktor ist derjenige mit dem niedrigsten Verhältnis aus verfügbarer Menge und festgelegtem Einsatzverhältnis.
4. Wo wird die Leontief-Funktion angewendet?
Hauptsächlich in der Input-Output-Analyse, um wirtschaftliche Zusammenhänge zwischen Sektoren zu untersuchen.
5. Kann die Leontief-Funktion in der Praxis abweichen?
Ja, in realen Produktionsprozessen gibt es oft Abweichungen durch Ineffizienzen oder Variationen bei den Einsatzfaktoren.
Zusammenfassung
Die Leontief-Produktionsfunktion beschreibt Produktionsprozesse mit fixen Einsatzverhältnissen, bei denen die Produktionsmenge durch den knappsten Faktor begrenzt wird. Sie eignet sich ideal zur Analyse von Produktionsengpässen und Effizienzsteigerungen. Durch die klare Struktur und Berechnungsmethode ist sie in der Wirtschaftsanalyse unverzichtbar.
In der Praxis zeigt die Leontief-Funktion ihre Stärke insbesondere in Bereichen wie der Agrarproduktion, der Nahrungsmittelindustrie und der Produktionsplanung. Sie bietet keine Flexibilität in der Faktorkombination, ist dafür jedoch ein präzises Werkzeug zur Optimierung von Ressourcen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






