[PR1] Gozintograph | Definition, Beispiele, Besonderheiten

Ein Gozintograph ist ein vielseitiges Werkzeug in der Produktionswirtschaft, das dazu dient, die Struktur und die Abläufe eines Produktionsprozesses grafisch darzustellen. Diese visuelle Methode ist essenziell, um Materialflüsse, Abhängigkeiten und Engpässe zu identifizieren und so die Effizienz von Produktionsprozessen zu steigern.

Was ist ein Gozintograph?

Definition

Was steckt hinter einem Gozintographen?

Der Begriff „Gozintograph“ leitet sich von der englischen Redewendung „goes into“ ab, was übersetzt „geht in“ bedeutet. Ein Gozintograph ist ein gerichteter Graph, bei dem:

Knoten Produktionsstufen oder Produkte repräsentieren.
Kanten die Inputs und Outputs zwischen den Produktionsstufen darstellen.

Das zentrale Ziel eines Gozintographen ist es, die Beziehungen zwischen einzelnen Fertigungsstufen zu verdeutlichen. Dabei gibt er an, welche Inputs (Rohstoffe, Halbfabrikate oder Baugruppen) in welchen Mengen erforderlich sind, um bestimmte Outputs (Zwischenprodukte oder Endprodukte) herzustellen.

Darstellung eines Gozintographen

Ein Gozintograph wird typischerweise als gerichteter Graph dargestellt. Die wichtigsten Elemente sind:

Knoten: Sie stehen für Produkte, Bauteile oder Produktionsstufen.
Kanten: Sie stellen die Verbindung zwischen den Knoten dar und geben an, wie viele Einheiten eines Produkts benötigt werden, um ein anderes Produkt herzustellen. Diese Werte werden häufig als Inputkoeffizienten bezeichnet.

Beispielhafte Darstellung:

In einem Produktionsprozess mit sechs Produkten (Knoten $y_1$ bis $y_6$ ) könnte ein Gozintograph wie folgt aussehen:

$y_1, y_2, y_3$ : Eingangsprodukte, die beschafft werden müssen.
$y_4, y_5$ : Zwischenprodukte, die aus $y_1, y_2, y_3$ hergestellt werden.
$y_6$ : Endprodukt, das aus den Zwischenprodukten $y_4$ und $y_5$ entsteht.

Die Materialflüsse zwischen den Produkten werden durch Pfeile dargestellt, die mit Stücklisten- oder Inputkoeffizienten versehen sind.

Merk’s dir!

Die Verwendung von Gozintographen kann in verschiedenen Phasen des Produktionsmanagements nützlich sein. In der Planungsphase ermöglicht der Gozintograph eine detaillierte Analyse der Fertigungsstruktur. Während der Produktion dient er als Referenzwerkzeug für die Steuerung und Überwachung von Materialflüssen. Auch bei der Optimierung von Produktionsprozessen können Gozintographen genutzt werden, um Effizienzsteigerungen zu identifizieren.

Insgesamt trägt der Gozintograph dazu bei, die Transparenz im Produktionsprozess zu verbessern und eine effiziente und effektive Produktionsplanung und -steuerung zu ermöglichen.

Damit du dir diesen Vorgang bildlich nachvollziehen kannst, stellen wir dir nun einen Gozintographen vor:

Im vorliegenden Diagramm sind sechs Produkte als Knoten repräsentiert. Die Materialflüsse zwischen diesen Produkten werden durch Pfeile dargestellt. Jeder Pfeil ist mit einer Zahl versehen, die die Stückmenge des in den nächsten Arbeitsschritt eingehenden Vorprodukts angibt.

Diese Zahlen werden als Stücklisten- oder Inputkoeffizienten bezeichnet ( $s_{ij}$ ), und die entsprechende Matrix $S = (s_{ij})_{6x6}$ wird als Stücklisten- oder Direktbedarfsmatrix bezeichnet:

Direktbedarfsmatrix

$S = \begin{pmatrix} 0 & 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 1 & 3 & 0 \\ 0 & 0 & 0 & 5 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 5 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}$ .

Die Matrix wird so gelesen: In der ersten Zeile ( $y_1$ ) gehen 6 Einheiten von $y_1$ in $y_5$ ein.)

Im unteren Teil der Knoten sind Outputmengen eingetragen, die entweder als Endprodukte oder Baugruppen auf den Absatzmarkt gelangen. Es ist deutlich erkennbar, dass die Knoten 1, 2 und 3 nicht direkt am Absatzmarkt verkauft werden. Stattdessen stellen sie Inputfaktoren dar, die beschafft werden müssen, um die Zwischenprodukte 4 und 5 herzustellen. Ein Teil dieser Zwischenprodukte wird am Absatzmarkt verkauft (z. B. Zwischenprodukt 4 mit 20 Einheiten), während ein anderer Teil für die Herstellung des Endprodukts benötigt wird (z. B. Zwischenprodukt 4 mit 2 Einheiten). Das Endprodukt wird schließlich am Absatzmarkt veräußert.

Stücklistenauflösung

Die Stücklistenauflösung bezieht sich auf den Prozess, in dem eine Stückliste oder ein Produktionsplan in seine einzelnen Bestandteile oder Komponenten aufgeschlüsselt wird. In der Produktionswirtschaft wird eine Stückliste verwendet, um die Materialien und Komponenten aufzulisten, die zur Herstellung eines bestimmten Produkts benötigt werden. Bei der Stücklistenauflösung wird diese Liste detailliert analysiert, um die genauen Mengen und Typen der erforderlichen Rohstoffe, Bauteile oder Baugruppen zu identifizieren.

Merk’s dir!

Die Stücklistenauflösung ist ein wichtiger Schritt in der Produktionsplanung und -steuerung. Sie ermöglicht es, den Bedarf an Materialien und Komponenten präzise zu ermitteln, was wiederum die Beschaffung, Lagerhaltung und Produktionsprozesse effizienter gestaltet.

Beziehen wir uns jetzt wieder auf unsere bisherige Betrachtung so folgt daraus:
Die Aufgabe der Stücklistenauflösung besteht darin, aus dem vorliegenden Primärbedarf $x_j$ mit (j=4, 5, 6) den gesamten Bruttobedarf y_i mit (i = 1, 2, 3, 4, 5, 6) zu berechnen.

Dabei repräsentiert der Bruttobedarf $y_i$ die Summe aus dem Primärbedarf $x_i$ und dem durch den Primärbedarf höherer Stufen verursachten Sekundärbedarf $s_i$ .

Formel

Formal lässt sich dies durch die Gleichung

Bedarf

$y_i = s_i + x_i$

mit (i = 1, 2, 3, 4, 5, 6) beschreiben.

Beispiel

Beispiel!

Die Berechnung des Bruttobedarfs beginnt auf der untersten Stufe des Gozintographen und führt zu einem Gleichungssystem mit sechs Gleichungen:

(1) $y_1 = 6 y_5 + 0$

(2) $y_2 = y_4 + 3 y_5 + 0$

(3) $y_3 = 5 y_4 + 0$

(4) $y_4 = 2 y_6 + 20$

(5) $y_5 = 2 y_6 + 15$

(6) $y_6 = 50$

Schreibt man diese Gleichungen als Matrizengleichung, erhält man $\vec{y} = S \vec{y} + \vec{x}$ mit

$\vec{y} : = \left(\begin{array}{c} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \end {array}\right)$ , sowie $\vec{x} : = \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end {array}\right) = \left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 20 \\ 15 \\ 50 \end {array}\right)$ .

Das Gesamtergebnis ergibt sich durch rückwärtiges Einsetzen:

(6) $y_6^* = 50$

(5) $y_5^* = 2 \cdot y_6 + 15 = 2 \cdot 50 + 15 = 115$

(4) $y_4^* = 2 \cdot y_6 + 20 = 2 \cdot 50 + 20 = 120$

(3) $y_3^* = 5 \cdot y_4 +0 = 5 \cdot 120 + 0 = 600$

(2) $y_2^* = y_4 + 3 \cdot y_5 + 0 = 120 + 3 \cdot 115 = 465$

(1) $y_1^* = 6 \cdot y_5 + 0 = 690$

Uns interessieren besonders die Werte $y_1^*,y_2^*,y_3^*$ , da sie die Verbrauchsfaktormengen $r_1 = y_1^*$ , $r_2 = y_2^*$ , $r_3 = y_3^*$ repräsentieren, die zur Produktion der Verkaufsprodukte $x_4=20, x_5 = 15$ und $x_6 = 50$ notwendig sind.

Diese Inputwerte ( $r_1, r_2 ,r_3$ ) werden auch als Einkaufsprogramm zum Produktionsprogramm ( $x_4 ,x_5, x_6$ ) bezeichnet, wobei $y_4^*$ und $y_5^*$ als Zwischenproduktmengen betrachtet werden.

Hinzunahme der Leontief-Produktionsfunktion

Zur Ermittlung der direkten Beziehung zwischen Enderzeugnissen und Vorprodukten wird die Leontief-Produktionsfunktion aufgestellt. Hierzu setzen wir $x_4 = x_5 = 0$ . (Das bedeutet, der Absatz der Baugruppen $y_4$ und $y_5$ wird nicht beachtet.)

Für die Enderzeugnisse gilt: $x_i \; \; ( i = 6)$

Für die Baugruppen gilt: $r_i \; \; ( i = 4,5)$

Für die Teile gilt: $r_i \; \; (i = 1,2,3)$

$r_1 = 6r_5$

$r_2 = r_4 + 3r_5$

$r_3 = 5r_4$

$r_4 = 2x_6$

$r_5 = 2x_6$

$r_1 = 6r_5 = 6(2x_6) = 18x_6$

$r_2 = r_4 + 3r_5 = 2x_6 + 3(2x_6) = 8x_6$

$r_3 = 5r_4 = 5(2x_6) = 10x_6$

Aus Produktionssicht bedeutet dies, dass zur Herstellung des Endprodukts 18 Einheiten von Rohstoff 1, 8 Einheiten von Rohstoff 2 und 10 Einheiten von Rohstoff 3 benötigt werden.

Wichtige Informationen über den Gozintographen

Stücklistenauflösung: Der Gozintograph ermöglicht eine detaillierte Analyse der Stücklisten, also der Auflistung aller Materialien und Komponenten, die für die Herstellung eines Produkts benötigt werden. Dies ist essenziell für die Planung von Materialbedarfen und Produktionsprozessen.
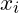Materialbedarfsberechnung: Mithilfe von Gleichungen wie $y_i = s_i + x_i$ lässt sich der gesamte Bruttobedarf berechnen, wobei $y_i$ den Gesamtbedarf, $s_i$ den Sekundärbedarf und $x_i$ den Primärbedarf beschreibt.
Leontief-Produktionsfunktion: Um die direkten Beziehungen zwischen Vorprodukten und Enderzeugnissen zu bestimmen, wird oft die Leontief-Produktionsfunktion angewendet. Diese ermöglicht die Berechnung der benötigten Rohstoffmengen auf Grundlage des geplanten Produktionsvolumens.

Anschauliche Beispiele für die Anwendung eines Gozintographen

Automobilindustrie: Ein Autohersteller verwendet einen Gozintographen, um die Beziehungen zwischen Rohstoffen (z. B. Stahl, Kunststoff), Baugruppen (z. B. Motor, Getriebe) und Endprodukten (Fahrzeuge) darzustellen. Dadurch kann der Hersteller Engpässe frühzeitig erkennen und die Materialflüsse optimieren.
Lebensmittelproduktion: In einer Bäckerei wird ein Gozintograph genutzt, um die Zutaten für verschiedene Backwaren zu planen. Beispielsweise zeigt der Graph, wie viel Mehl, Zucker und Butter benötigt werden, um bestimmte Mengen an Brot und Kuchen herzustellen.
Elektrogerätefertigung: Ein Hersteller von Smartphones verwendet einen Gozintographen, um die Beziehung zwischen elektronischen Bauteilen (z. B. Prozessor, Akku) und Baugruppen (z. B. Platinen, Gehäuse) darzustellen. Dies hilft, die Logistik und Lagerhaltung effizient zu gestalten.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

Wofür wird ein Gozintograph hauptsächlich verwendet?

Ein Gozintograph wird verwendet, um Produktionsprozesse zu visualisieren, Materialflüsse zu analysieren und Abhängigkeiten zwischen Produktionsstufen zu erkennen.

Welche Vorteile bietet ein Gozintograph?

Verbesserung der Transparenz in der Produktionsplanung.
Unterstützung bei der Identifikation von Engpässen.
Optimierung der Materialbedarfsplanung.

Wie wird ein Gozintograph erstellt?

Identifikation aller Produktionsstufen und Materialien.
Festlegung der Beziehungen zwischen Inputs und Outputs.
Erstellung eines gerichteten Graphen, der diese Beziehungen darstellt.

In welchen Branchen ist der Gozintograph besonders nützlich?

Der Gozintograph findet Anwendung in vielen Branchen, darunter Automobilindustrie, Maschinenbau, Lebensmittelproduktion und Elektronikfertigung.

Kann ein Gozintograph auch für Dienstleistungen verwendet werden?

Ja, in abgewandelter Form. Bei Dienstleistungen können Inputs (z. B. Arbeitsstunden) und Outputs (z. B. erbrachte Leistungen) ebenfalls grafisch dargestellt werden.

Zusammenfassung

Ein Gozintograph ist ein leistungsstarkes Werkzeug, um Produktionsprozesse zu planen, zu analysieren und zu optimieren. Durch die grafische Darstellung der Beziehungen zwischen Inputs und Outputs bietet er Einblicke in Materialflüsse, Abhängigkeiten und Engpässe. Dies ermöglicht Unternehmen, ihre Produktionsabläufe effizienter zu gestalten und Kosten zu senken.

Mit seiner Anwendung in verschiedenen Branchen, von der Automobilindustrie bis hin zur Lebensmittelproduktion, ist der Gozintograph ein unverzichtbares Hilfsmittel für moderne Produktionsplanung und -steuerung.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++