Die degressive Kostenfunktion beschreibt eine Situation, in der die durchschnittlichen variablen Kosten pro Einheit mit zunehmender Produktionsmenge abnehmen. Dieser Effekt resultiert aus verschiedenen Skaleneffekten, die Unternehmen nutzen, um ihre Produktionskosten zu senken.
Was ist eine degressive Kostenfunktion?
Definition
Die degressive Kostenfunktion spiegelt eine Situation wider, in der die Kosten pro Einheit abnehmen, je mehr Einheiten produziert werden. Dieser Effekt entsteht durch eine unterproportionale Zunahme der variablen Kosten im Vergleich zur Produktionsmenge. Anders ausgedrückt: Je mehr Einheiten produziert werden, desto geringer sind die durchschnittlichen variablen Kosten pro Einheit.
Ein klassisches Beispiel hierfür sind Rabatte bei hohen Bestellmengen, die Unternehmen dabei helfen, ihre Gesamtkosten zu reduzieren.
Formel
Die allgemeine Formel für die degressive Kostenfunktion lautet:
Hierbei sind:
die Gesamtkosten in Abhängigkeit von der Produktionsmenge x,
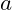ist eine positive Konstante, die die Ausprägung der degressiven Kosten beschreibt,
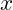ist die Produktionsmenge,
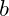sind die fixen Kosten.
Beispiel 1:
Angenommen, ein Unternehmen hat fixe Kosten von 500 Euro und eine degressive Variable-Kosten-Konstante von 100. Die degressive Kostenfunktion lautet:
Hierbei sind:
die Gesamtkosten in Abhängigkeit von der Produktionsmenge x,
repräsentiert die degressiven variablen Kosten (100 multipliziert mit der Wurzel der Produktionsmenge x),
sind die fixen Kosten.
Bedeutung:
Die degressive Kostenfunktion spiegelt eine Situation wider, in der die Skaleneffekte zu sinkenden variablen Kosten pro Einheit führen, wenn die Produktionsmenge zunimmt. Unternehmen können von dieser Funktion profitieren, da sie niedrigere Durchschnittskosten pro Einheit bei höheren Produktionsmengen ermöglicht. Dies kann die Wettbewerbsfähigkeit stärken und zu höheren Gewinnspannen führen. Das bedeutet, dass mit steigender Produktion die durchschnittlichen Kosten sinken. Grund dafür ist die Verteilung der Fixkosten auf die Menge (Fixkostendegression).
Beispiel 2:
Ein Unternehmen hat die folgende Kostenfunktion: 
.
Diese Funktion repräsentiert eine degressive Kostenfunktion.
Die variablen Kosten belaufen sich auf 100 € bei der Produktion einer Einheit und steigen auf 141 € bei der Produktion von zwei Einheiten. Bei einer Erhöhung der Produktionsmenge um 100% erhöhen sich die variablen Kosten lediglich um 41%. Dies deutet darauf hin, dass die variablen Kosten unterproportional zur Produktionsmenge ansteigen.
Die variablen Durchschnittskosten 
können durch die Funktion 
berechnet werden. Das bedeutet, dass die variablen Stückkosten mit zunehmender Produktionsmenge abnehmen.
Die Grenzkosten 
werden durch 
dargestellt. Auch die Grenzkosten zeigen einen abnehmenden Trend mit steigender Produktionsmenge.
Die gesamten durchschnittlichen Kosten 
setzen sich aus den variablen Kosten (
) und den fixen Kosten (
) zusammen.
In der Grafik kannst du erkennen, dass die Grenzkosten GK unter den durchschnittlichen variablen Kosten DVK liegen. Beide sinken mit steigender Produktionsmenge.
Beispiel 3:
Angenommen, ein Unternehmen stellt Laptops her, und die variablen Kosten pro Laptop betragen zu Beginn 800 €. Durch verbesserte Prozesse, effizientere Maschinen und Erfahrung in der Produktion sinken die variablen Kosten pro Laptop aufgrund von Skaleneffekten und Lernkurveneffekten. Nach einer bestimmten Produktionsmenge könnten die variablen Kosten pro Laptop beispielsweise auf 700 € fallen. In diesem Fall wäre die Kostenfunktion degressiv und könnte durch eine Formel wie 
dargestellt werden, wobei x die Anzahl der produzierten Laptops ist. Jeder zusätzliche Laptop würde dann geringere variable Kosten verursachen, was auf eine deg. Kostenfunktion hinweist.
Ursachen für eine degressive Kostenfunktion
-
Skaleneffekte und Spezialisierung: Mit steigender Produktionsmenge werden Ressourcen effizienter genutzt, und die Fixkosten verteilen sich auf eine größere Menge.
-
Economies of Scale: Größere Produktionsmengen senken die Durchschnittskosten pro Einheit, da Prozesse optimiert werden.
-
Lernkurveneffekt: Arbeiter und Maschinen werden mit der Zeit effizienter, was die Kosten weiter reduziert.
-
Rabatte und Mengenabnahme: Zulieferer bieten bei großen Bestellungen häufig Preisnachlässe an, die zu geringeren variablen Kosten führen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was unterscheidet die degressive von der progressiven Kostenfunktion?
Die deg. Kostenfunktion beschreibt abnehmende Durchschnittskosten pro Einheit mit steigender Produktionsmenge, während die progressive Kostenfunktion ansteigende Kosten pro Einheit darstellt, meist durch steigende variable Kosten bei erhöhter Produktion.
2. Welche Branchen profitieren besonders von einer degressiven Kostenfunktion?
Industriezweige wie die Automobil- oder Elektronikproduktion, bei denen Skaleneffekte und Lernkurven eine große Rolle spielen, profitieren besonders. Auch Handelsunternehmen, die von Mengenrabatten profitieren, können Vorteile erzielen.
3. Gibt es Einschränkungen der degressiven Kostenfunktion?
Ja, die deg. Kostenfunktion ist nicht unbegrenzt anwendbar. Nach einer bestimmten Produktionsmenge können Kosten nicht weiter sinken, oder es entstehen neue Fixkosten, z. B. durch die Anschaffung weiterer Maschinen.
4. Wie können Unternehmen die degressive Kostenfunktion nutzen?
Unternehmen können durch Prozessoptimierungen, Skaleneffekte und strategische Lieferantenauswahl ihre Durchschnittskosten senken und dadurch Wettbewerbsvorteile erzielen.
5. Welche Rolle spielen Fixkosten bei der degressiven Kostenfunktion?
Fixkosten sind ein zentraler Bestandteil, da sie sich bei steigender Produktionsmenge auf mehr Einheiten verteilen und so die durchschnittlichen Gesamtkosten reduzieren.
Zusammenfassung
Die degressive Kostenfunktion ist ein wichtiger Bestandteil der Kostenrechnung und hilft Unternehmen, ihre Produktionskosten zu analysieren und zu optimieren. Durch den Effekt sinkender Durchschnittskosten bei steigender Produktionsmenge können Unternehmen ihre Wettbewerbsfähigkeit stärken und Gewinne maximieren.
Ursachen wie Skaleneffekte, Economies of Scale und der Lernkurveneffekt spielen dabei eine entscheidende Rolle. Beispiele aus der Praxis zeigen, wie Unternehmen diese Funktion nutzen, um ihre Kostenstruktur zu verbessern. Die Kenntnis über die degressive Kostenfunktion ermöglicht es Unternehmen, strategische Entscheidungen zur Produktionsplanung und Prozessoptimierung zu treffen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team