PH1 – Kosinussatz

Der Kosinussatz stellt eine Beziehung zwischen den drei Seiten eines Dreiecks und einem Winkeln her. Ziel ist es also zum Beispiel aus zwei gegebenen Seiten und einem Winkel die dritte Seite zu berechnen. Wir betrachten hier keine rechtwinkligen Dreiecke mehr, sondern allgemeine Dreiecke.

Für ein optimales Verständnis hilft dir ein Videoclip zu dem Thema. Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH1 – Grundlagen der Physik.

Kosinussatz – Grundlagen

Der Kosinussatz stellt eine Beziehung zwischen den drei Seiten eines Dreiecks und einem Winkeln her. Ziel ist es also zum Beispiel aus zwei gegebenen Seiten und einem Winkel die dritte Seite zu berechnen. Wir betrachten hier keine rechtwinkligen Dreiecke mehr, sondern ein allgemeines Dreieck.

Der Kosinussatz wird außerdem innerhalb der Statik bei der Bestimmung der resultierenden Kraft aus zwei gegebenen Kräften (nicht rechtwinklig) benötigt. Innerhalb unseres Onlinekurses PH2 – Grundlagen der Statik wird gezeigt, wie mittels Kosinussatz die resultierende Kraft aus zwei Kräften mit Winkel bestimmt wird.

Allgemeines Dreieck zur Berechnung einer Seite - Kosinussatz — Allgemeines Dreieck

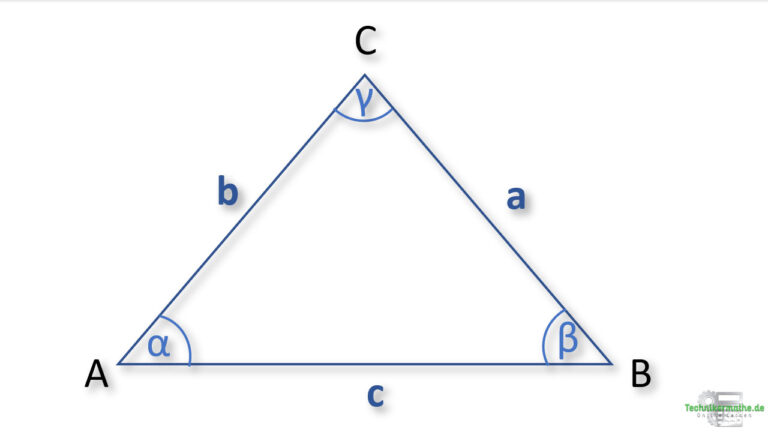
In der obigen Grafik ist das allgemeine Dreieck gegeben. Wir können mittels Kosinussatz eine Seite dieses Dreiecks berechnen, wenn zwei Seiten und ein Winkel gegeben sind.

Kosinussatz – Seite berechnen

Wollen wir zum Beispiel die Seite c berechnen, so müssen die Seiten a und b sowie der eingeschlossene Winkel γ gegeben sein. Der Kosinussatz lautet dann:

$c = \sqrt{a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(\gamma)}$ Berechnung von Seite c

Die anderen Seiten können natürlich ebenfalls mit dem Kosinussatz berechnet werden:

$a = \sqrt{b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(\alpha)}$ Berechnung von Seite a

$b = \sqrt{a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(\beta)}$ Berechnung von Seite b

Videoclip: Kosinussatz anwenden

Wie genau du mittels Kosinussatz eine Seite berechnest, zeige ich dir im folgenden Video:

Kosinussatz – Winkel berechnen

Wir können außerdem die Winkel im allgemeinen Dreieck berechnen, wenn wir drei Seiten gegeben haben. Dazu müssen wir die obigen Gleichungen nach den Winkeln umstellen:

$\cos(\gamma) = \dfrac{a^2 + b^2 - c^2 }{2 \cdot a \cdot b}$

$\cos(\alpha) = \dfrac{b^2 + c^2 - a^2 }{2 \cdot b \cdot c}$

$\cos(\beta) = \dfrac{a^2 + c^2 - b^2 }{2 \cdot a \cdot c}$

Auf der linken Seite steht nicht der Winkel, sondern der Kosinus vom Winkel. Um den Winkel zu erhalten, müssen wir die Umkehrfunktion des Kosinus anwenden, den Arkuskosinus.

Wir erhalten dann die drei Gleichungen zur Berechnung der drei Winkel im allgemeinen Dreieck:

$\gamma = \cos^{-1}(\dfrac{a^2 + b^2 - c^2 }{2 \cdot a \cdot b})$

$\alpha = \cos^{-1}(\dfrac{b^2 + c^2 - a^2 }{2 \cdot b \cdot c})$

$\beta = cos^{-1}(\dfrac{a^2 + c^2 - b^2 }{2 \cdot a \cdot c})$

Aufgaben zum Kosinussatz

Damit du eine Seite oder einen Winkel in einem allgemeinen Dreieck auf Anhieb berechnen kannst, betrachten wir im Folgenden vier Aufgaben zum Kosinussatz. Die oben angegebenen Gleichungen benötigst du, um die Aufgaben zum Kosinussatz lösen zu können. Versuche zunächst die Aufgaben selbstständig zu lösen, bevor du die Lösungen hinzuziehst.

Beispiel 1 : Seite berechnen

Aufgabenstellung

Aufgaben zum Kosinussatz — Beispiel 1: Kosinussatz

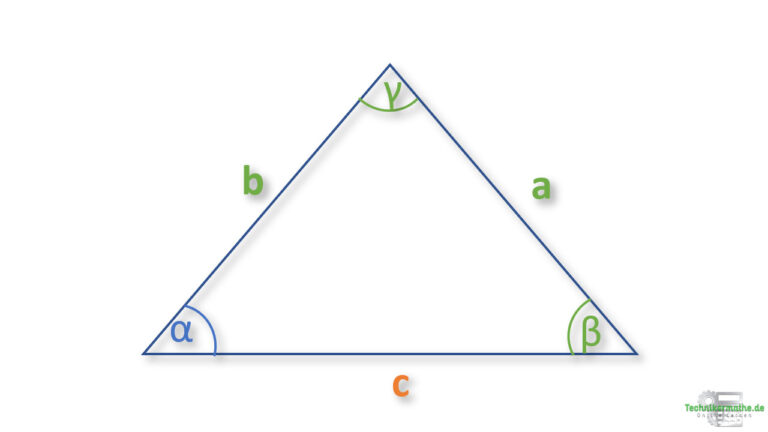
Gegeben sei das obige allgemeine Dreieck mit den Seiten a, b und c sowie den Winkeln α, β und γ.

Gegeben seien:

a = 6cm, b = 4,5 cm, γ = 60° und β = 40°.

Berechne die Seite c!

Lösung

Zur Berechnung der Seite c werden die Seiten a und b benötigt sowie der gegenüberliegende Winkel γ der gesuchten Seite c:

$c = \sqrt{a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(\gamma)}$

Danach setzen wir die gegebenen Werte ein:

$c = \sqrt{(6cm)^2 + (4,5cm)^2 - 2 \cdot 6 cm \cdot 4,5 cm \cdot \cos(60^\circ)} = 5,41 cm$

Die Angabe des Winkels β in der Aufgabenstellung erfolgte nur, um zu testen, ob du auch den richtigen Winkel auswählst.

Beispiel 2 : Winkel berechnen

Aufgabenstellung

Winkel in einem allgemeinen Dreieck berechnen - Aufgaben zum Kosinussatz — Aufgaben zum Kosinussatz

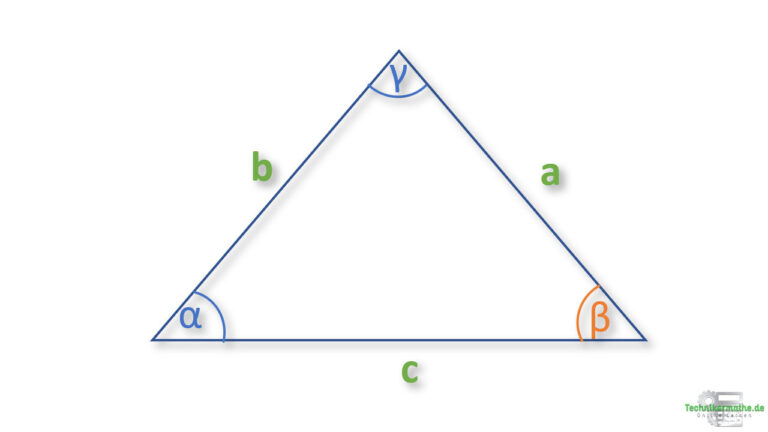
Gegeben sei das allgemeine Dreieck mit den Seiten a, b und c sowie den Winkeln α, β und γ.

Gegeben seien:

a = 5cm, b = 6,5 cm und c = 7 cm.

Berechne den Winkel β!

Lösung

Zur Berechnung des Winkels β werden alle drei Seiten benötigt. Es wird die folgende Gleichung verwendet:

$\beta = \cos^{-1} (\dfrac{a^2 + c^2 - b^2}{2 \cdot a \cdot c})$

Im Zähler addierst du zunächst die beiden quadrierten Seiten a² und b², die den Winkel $\beta$ einschließen. Danach ziehst du die dem gesuchten Winkel gegenüberliegender quadrierte Seite b² ab. Im Nenner tauchen nur die beiden Seite a und c auf, die den gesuchten Winkel $\beta$ einschließen.

Danach setzt du die gegebenen Werte ein:

$\beta = \cos^{-1} (\dfrac{(5 cm)^2 + (7 cm)^2 - (6,5 cm)^2}{2 \cdot 5 cm \cdot 7 cm}) = 63,03 ^\circ \approx 63 ^\circ$

Der Winkel $\beta$ beträgt 63°.

Beispiel 3 : Seite berechnen

Aufgabenstellung

Seite in einem allgemeinen Dreieck berechnen — Aufgaben zum Kosinussatz

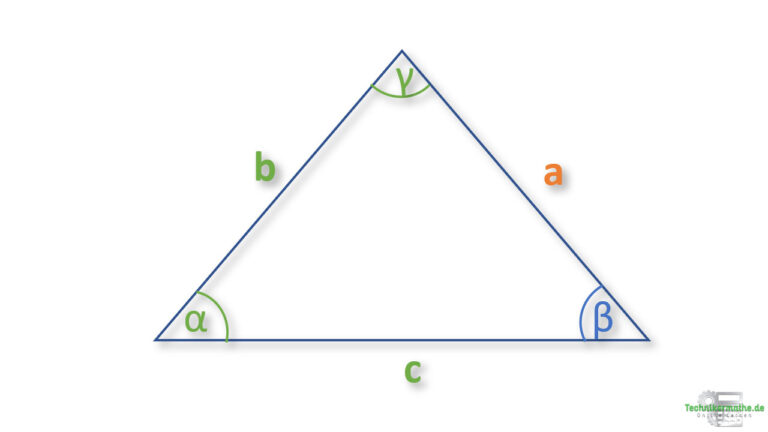
Gegeben sei das obige Dreieck mit den Seiten a, b und c sowie den Winkeln α, β und γ.

Gegeben seien:

b = 3,5 cm, c = 2 cm sowie α = 40° und γ= 70°.

Berechne die Seite a!

Lösung

Zur Berechnung der Seite a werden die Seiten b und c benötigt sowie der gegenüberliegende Winkel α der gesuchten Seite a:

$a = \sqrt{b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(\alpha)}$

Als nächstes setzt du die gegebenen Werte ein:

$a = \sqrt{((3,5 cm)^2 + (2 cm)^2 - 2 \cdot 3,5cm \cdot 2 cm \cdot \cos(40^\circ)} = 2,35 cm$

Die Seite a ist 2,35 cm lang.

Beispiel 4 : Seite berechnen

Aufgabenstellung

Aufgabe 4: Parallelogramm und Kosinussatz — Aufgaben zum Kosinussatz: Parallelogramm und Kosinussatz

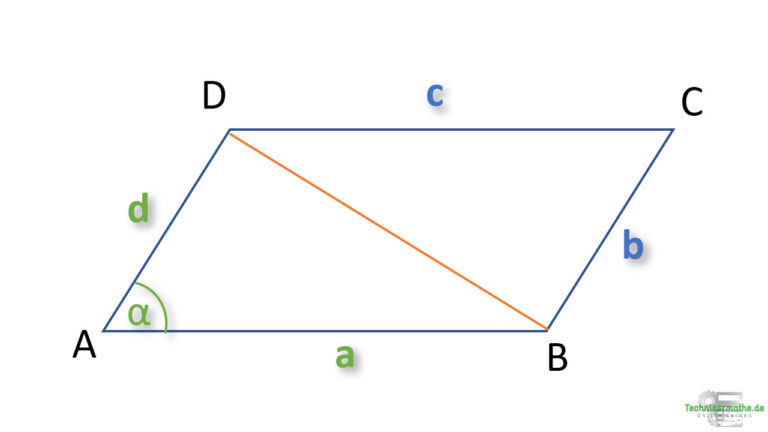
Gegeben sei das obige Parallelogramm. Gegeben seien die Seite $a = 12cm$ und $d = 4 cm$ . Der Winkel $\alpha$ beträgt 55°.

Berechne die Länge der Diagonalen DB!

Lösung

Wir können hier den Kosinussatz anwenden um die Länge der Diagonalen zu bestimmen. Die Diagonale teilt das Parallelogramm in zwei gleich große allgemeine Dreiecke. Wie haben die beiden Seiten $a$ und $d$ sowie den eingeschlossenen Winkel $\alpha$ gegeben.

Die Diagonale liegt also genau gegenüber von unserem gesuchten Winkel. Wir bezeichnen diese als $\overline{DB}$ und wenden den folgenden Kosinussatz an:

$\overline{DB} = \sqrt{a^2 + d^2 - 2 \cdot a \cdot d \cdot \cos(\alpha)}$

Einsetzen der gegebenen Werte:

$\overline{DB} = \sqrt{(12 cm)^2 + (4 cm^2)^2 - 2 \cdot 12 cm \cdot 4 cm \cdot \cos(55^\circ)}$

$\overline{DB} = 10,24 cm$ .

Die Diagonale hat eine Länge von 10,24 cm.

Tausende interaktive Übungsaufgaben

Übungsbereich

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++