[ME1] Zusammengesetzte Beanspruchung [Erklärung, Beispiele, Berechnungen]

In diesen Kursabschnitt befassen wir uns ausführlich mit dem Thema Zusammengesetzte Beanspruchung. Dabei gehen wir auf Normalspannungen, Schubspannungen, Spannungsaddition, Spannungstensor, Spannungszustände und Hauptspannungszustände sowie Vergleichsspannungen im Detail ein.

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Zusammengesetzte Beanspruchung – Grundlagen

Die “Zusammengesetzte Beanspruchung” ist ein wichtiges Thema in der Festigkeitslehre und bezieht sich auf die gleichzeitige Anwendung von verschiedenen Arten von mechanischen Belastungen auf ein Bauteil oder Material.

Unterliegt eine Konstruktion mehreren Grundbeanspruchungsarten zur gleichen Zeit, so führt dies infolge einer Überlagerung der einzelnen Beanspruchungen zu einer komplexen und mehrdimensionalen Spannungsverteilung.

Merk’s dir!

In der Festigkeitslehre wird untersucht, wie verschiedene Arten von Belastungen die strukturelle Integrität eines Bauteils beeinflussen können. Dabei gibt es zwei Haupttypen von Belastungen:

Zug (Spannung)
Druck (Druckspannung),
sowie Scherbelastung.

Die Zusammengesetzte Beanspruchung tritt auf, wenn ein Bauteil sowohl Zug- als auch Druckbelastungen sowie Scherbelastungen gleichzeitig erfährt.

Zusammengesetzte Beanspruchung - Bestandteile eines Spannungstensors — Zusammengesetzte Beanspruchung – Bestandteile eines Spannungstensors

Dies kann in realen Strukturen und Bauteilen häufig vorkommen.

Beispiel: Stahlträger

Zum Beispiel kann ein Träger in einer Brücke sowohl axial (in Längsrichtung) belastet sein als auch quer zur Längsrichtung durch Querkräfte (Scherkräfte).

In solchen Fällen müssen Ingenieure und Techniker die kombinierten Auswirkungen dieser Belastungen auf die Festigkeit des Bauteils berücksichtigen.

Wie lösen wir das Problem?

Die Festigkeitslehre bietet uns verschiedene Theorien und Ansätze, um die Auswirkungen der Zusammengesetzten Beanspruchung zu analysieren und sicherzustellen, dass ein Bauteil die erforderliche Festigkeit und Steifigkeit aufweist, um den Belastungen standzuhalten.

Dazu gehören

Mohrsche Spannungskreistheorie,
Maximale-Spannung-Theorie und
Tresca-Theorie,

die je nach den spezifischen Anforderungen und Materialien verwendet werden.

Ingenieure und Techniker verwenden diese Konzepte, um Bauteile zu entwerfen und zu analysieren, um sicherzustellen, dass sie den auftretenden Belastungen standhalten können, ohne zu versagen. Dies ist entscheidend in vielen Bereichen der Ingenieurwissenschaften, einschließlich des Bauwesens, der Luft- und Raumfahrt, der Maschinenbau und der Materialwissenschaften.

Normalspannungen

Die Normalspannung bezieht sich innerhalb der Festigkeitslehre auf die Spannungskomponente, die senkrecht zur Querschnittsfläche eines Materials oder Bauteils wirkt. Ursache: Zug-, Druck-, Biegebelastungen

Sie tritt auf, wenn eine mechanische Belastung in Richtung der Fläche wirkt, die senkrecht zu dieser Fläche steht.

Die Normalspannung wird oft mit dem griechischen Buchstaben $\sigma$ [Sigma] dargestellt und kann positiv oder negativ sein, abhängig davon, ob es sich um eine Zug- oder Druckspannung handelt.

Formen der Normalspannungen

Hier sind die Erläuterungen zur Normalspannung:

Zugspannung (positive Normalspannung): Wenn eine Kraft auf ein Material in Zugrichtung wirkt, dehnt sich das Material aus. Die Spannung in diesem Fall wird als Zugspannung bezeichnet und ist positiv. Sie wird in der Regel in Pascal (Pa) oder Megapascal (MPa) gemessen.
Druckspannung (negative Normalspannung): Wenn eine Kraft auf ein Material in Druckrichtung wirkt, wird das Material zusammengedrückt. Die Spannung in diesem Fall wird als Druckspannung bezeichnet und ist negativ. Sie wird ebenfalls in Pascal oder Megapascal gemessen, aber mit einem negativen Vorzeichen.

Berechnung der Normalspannungen

Normalspannungen

Die Berechnung der Normalspannung erfolgt mithilfe der folgenden Formel:

$\sigma = \frac{F}{A}$

Kennzahlen:

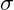$\sigma$ : Normalspannung in Pascal (Pa) oder Megapascal (MPa).
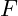$F$ : Die auf das Material wirkende Kraft in Newton (N).
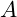$A$ : Die Querschnittsfläche des Materials, die von der Kraft durchquert wird, in Quadratmetern (m²).

Merk’s dir!

Es ist wichtig zu beachten, dass die Normalspannung nur eine der Spannungskomponenten ist, die in einem Bauteil auftreten können. In komplexen Belastungssituationen, wie der Zusammengesetzten Beanspruchung, müssen alle Spannungskomponenten berücksichtigt werden, um die Festigkeit und Stabilität eines Bauteils zu analysieren und zu bewerten.

Die Kenntnis der Normalspannung bildet die Grundlage für viele Festigkeitsberechnungen und -analysen in der Ingenieurwissenschaft.

Schubspannungen

Die Schubspannung bezieht sich auf die Spannungskomponente, die parallel zur Querschnittsfläche eines Materials oder Bauteils wirkt.

Anders als die Normalspannung, die senkrecht zur Fläche wirkt, verursacht die Schubspannung eine Verschiebung oder Scherung der Materialpartikel in der Fläche. Die Schubspannung wird oft mit dem griechischen Buchstaben $\tau$ (Tau) dargestellt und in Pascal (Pa) oder Megapascal (MPa) gemessen.

Formen der Schubspannung

Hier sind Erläuterungen zur Schubspannung:

Scherbelastung: Die Schubspannung tritt auf, wenn Kräfte in entgegengesetzte Richtungen auf benachbarte Materialpartikel wirken, die parallel zur Querschnittsfläche angeordnet sind. Dies führt dazu, dass die Materialpartikel in der Ebene gegeneinander verschoben werden, wodurch eine Scherbelastung entsteht.
Schubspannungsberechnung: Die Schubspannung wird berechnet, indem die auf das Material wirkende Schubkraft durch die Querschnittsfläche geteilt wird, die senkrecht zur Schubkraft steht.

Berechnung der Schubspannung

Schubspannungen

Die Berechnung der Schubspannung erfolgt mithilfe der folgenden Formel:

$\tau = \frac{F}{A}$

Kennzahlen

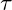$\tau$ : Die Schubspannung in Pascal (Pa) oder Megapascal (MPa).
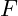$F$ : Die Schubkraft, die auf das Material wirkt, in Newton (N).
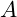$A$ : Die Fläche, die senkrecht zur Schubkraft steht, in Quadratmetern (m²).

Merk’s dir!

Die Schubspannung ist insbesondere wichtig bei der Analyse von Bauteilen, die Scherkräften ausgesetzt sind, wie zum Beispiel Balken, die sich unter Querbelastungen oder Torsion befinden. Sie spielt auch eine Rolle in der Zusammengesetzten Beanspruchung, wo sowohl Normalspannungen als auch Schubspannungen auftreten können.

Spannungsaddition

Die Spannungsaddition ist ein wichtiger Aspekt in der Festigkeitslehre und bezieht sich auf die Berechnung und das Verständnis der Gesamtspannung in einem Material oder Bauteil, das verschiedenen Arten von Belastungen ausgesetzt ist.

In vielen praktischen Anwendungen wirken gleichzeitig Normalspannungen (Zug- oder Druckspannungen) und Schubspannungen auf ein Bauteil. Die Spannungsaddition ermöglicht die Ermittlung der Gesamtspannung, die aus dieser Kombination von Belastungen resultiert.

Ansätze der Spannungsaddition

Es gibt zwei grundlegende Ansätze zur Spannungsaddition:

Betrag der Gesamtspannung (Von Mises-Spannung)

Die Von-Mises-Spannung oder auch äquivalente Spannung ist eine Methode zur Berechnung der Gesamtspannung in einem Bauteil, das sowohl Normalspannungen als auch Schubspannungen erfährt.

Diese Methode berücksichtigt die unterschiedlichen Spannungsarten und ihre relativen Einflüsse auf das Versagen des Materials.

Die Formel zur Berechnung der Von-Mises-Spannung lautet:

$\sigma = \sqrt{(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2 + 3 (\tau_1^2 + \tau_2^2 + \tau_3^2) }$

Kennzahlen:

$\sigma_1, \sigma_2, \sigma_3$ : Die Hauptnormalspannungen (Hauptspannungen) im Material.
$\tau 1, \tau_2, \tau_3$ : Die Schubspannungen (Scherspannungen) im Material.

Diese Methode geht davon aus, dass das Material bei Versagen nicht bei einer bestimmten Normalspannung oder Schubspannung versagt, sondern bei einer bestimmten äquivalenten Spannung, die aus allen auf das Material wirkenden Spannungen resultiert. Die Von-Mises-Spannung wird dann mit einem zulässigen Spannungsmaßstab verglichen, um zu beurteilen, ob das Material versagensgefährdet ist.

Maximale Spannungsaddition:

Ein anderer Ansatz zur Spannungsaddition besteht darin, die verschiedenen Spannungsarten (Normalspannungen und Schubspannungen) separat zu betrachten und ihre maximalen Werte zu ermitteln. Dies bedeutet, dass die größte Normalspannung und die größte Schubspannung unabhängig voneinander betrachtet werden, um sicherzustellen, dass sie innerhalb der zulässigen Werte liegen.

Die Spannungsaddition ist entscheidend, um die Sicherheit und Integrität von Bauteilen und Strukturen zu gewährleisten. Durch die Berücksichtigung aller auf das Material wirkenden Spannungen und die Anwendung geeigneter Kriterien können Ingenieure sicherstellen, dass ein Bauteil den erforderlichen Festigkeitsanforderungen entspricht und nicht versagt.

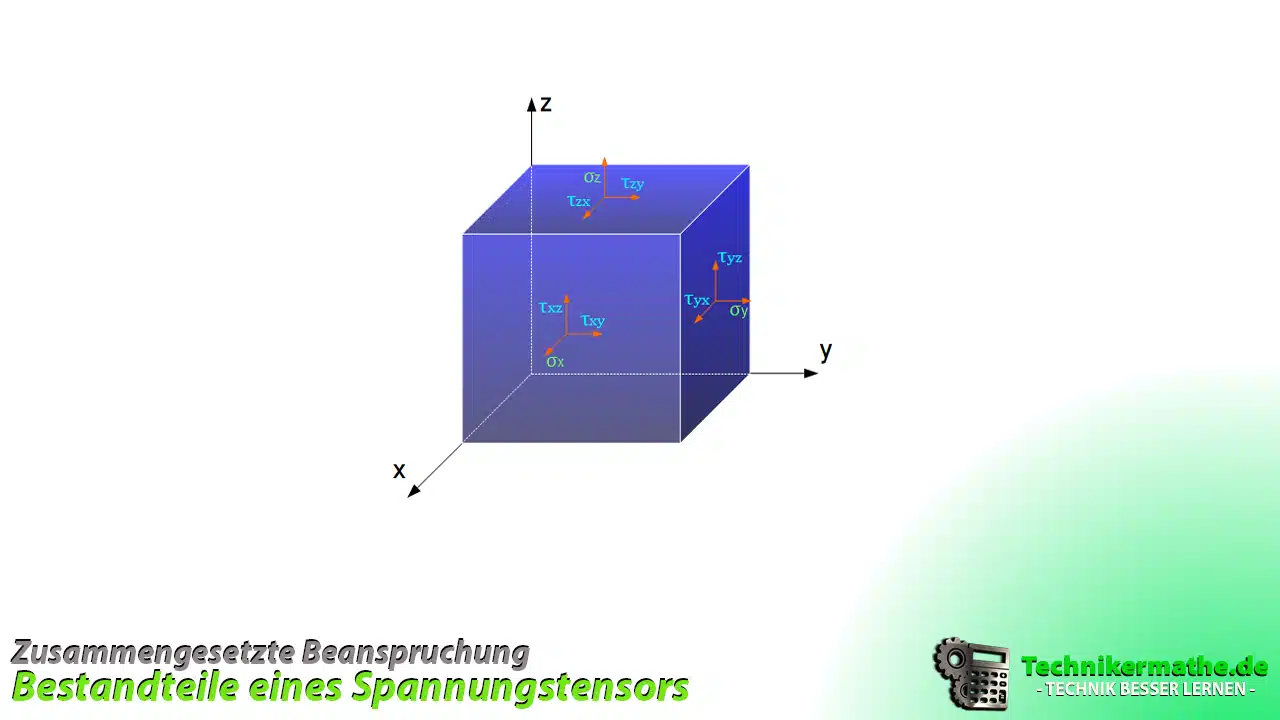
Spannungstensor

Addiert man die Spannungskomponenten miteinander, so ergibt sich daraus der Spannungszustand, der innerhalb eines Spannungstensors $\gamma$ zusammenfassend visualisiert wird.

Der Spannungstensor wird verwendet, um die Spannungsverteilung in einem dreidimensionalen Festkörper oder einem Kontinuum darzustellen. Der Spannungstensor ist ein mathematisches Instrument, das Ingenieure und Techniker verwenden, um die inneren Kräfte und Spannungen in einem Material zu analysieren und zu verstehen.

Darstellung des Spannungstensors

Der Spannungstensor ist eine Matrix, die die Spannungen in einem Material oder einem Festkörper in verschiedenen Raumrichtungen beschreibt. In einem dreidimensionalen Raum sind die Spannungen in der Regel durch eine 3×3-Matrix dargestellt.

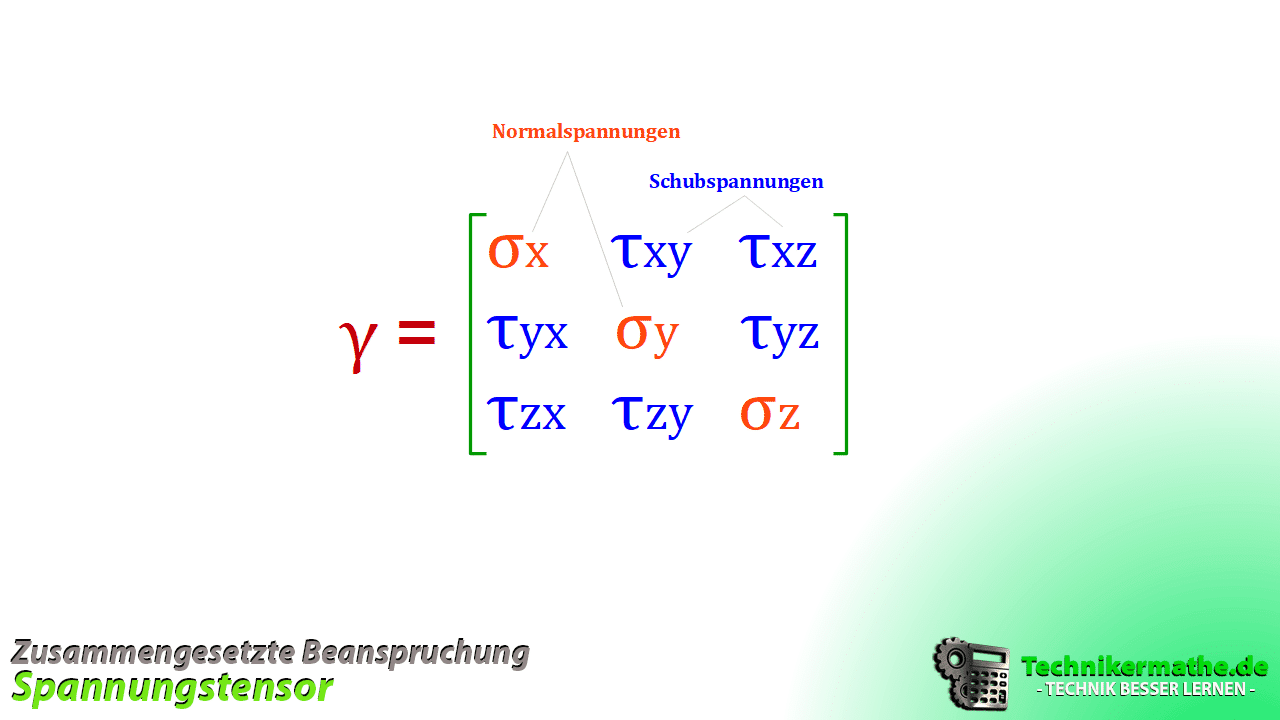
Spannungstensor mit 3x3 Matrix — Spannungstensor mit 3×3 Matrix

Spannungskomponenten des Spannungstensors

Der Spannungstensor enthält neun Hauptspannungskomponenten, von denen drei die Normalspannungen sind, die entlang der Hauptachsen des Koordinatensystems wirken, und sechs die Schubspannungen sind, die die Scherbelastungen in verschiedenen Richtungen repräsentieren.

Die Hauptnormalspannungen werden oft als σ_x, σ_y und σ_z bezeichnet, wobei x, y und z die Koordinatenachsen sind.
Die Schubspannungen werden als τ_xy, τ_yz, τ_zx, τ_yx, τ_zy und τ_xz bezeichnet.

Bilanzgleichung des Spannungstensors

Der Spannungstensor muss die statische und dynamische Gleichgewichtsbedingungen im Material erfüllen. Dies bedeutet, dass die Summe der Kräfte und Momente in jedem Materialvolumen gleich Null sein muss, um die Gleichgewichtsbedingungen zu erfüllen.

Spannungszustände

In der Praxis wird nicht selten auf die Berechnung des vollständigen Spannungszustands in der Praxis verzichtet, da diese sehr zeit- und rechenaufwendig ist.

So erfordert die Berechnung bei finiten Elementen mit räumlichen Elementen bedingt große Speicher und Rechenzeiten in EDV-Anlagen. Es wird daher im Vorfeld genau untersucht ob die Spannungen in mindestens einer von drei Richtungen vernachlässigbar klein ist.

Dies erlaubt eine Beschränkung auf
• einachsiger Spannungszustand (Eindimensionaler Spannungszustand (Axialspannung)) : Dies tritt auf, wenn eine Belastung axial, also in Längsrichtung, auf ein Bauteil wirkt. Das Material wird entweder gedehnt (positiv) oder zusammengedrückt (negativ) entlang seiner Längsachse. Die Normalspannung ist in diesem Fall die dominierende Spannungskomponente.
• zweiachsiger Spannungszustand (Zweidimensionaler Spannungszustand) : In diesem Zustand wirken Belastungen in zwei Richtungen. Zum Beispiel kann ein flacher Balken unter einer Biegebelastung stehen, wodurch Normalspannungen in der Höhe und Schubspannungen in der Ebene des Balkens entstehen.

vollständig ist die Liste mit:

dreiachsiger Spannungszustand (Dreidimensionaler Spannungszustand) : Hier wirken Belastungen in allen drei Raumrichtungen. Ein Beispiel ist eine Kugel unter innerem Druck, bei der alle neun Hauptspannungskomponenten des Spannungstensors relevant sind.
Torsion : Torsion tritt auf, wenn eine Drehkraft auf ein Bauteil wirkt. Dies erzeugt Schubspannungen in der Querschnittsebene des Bauteils.
Triaxialer Spannungszustand : In dieser Situation sind alle drei Hauptnormalspannungen unterschiedlich. Ein Beispiel dafür ist eine Probe, die sowohl axial gestaucht als auch seitlich eingeschränkt wird.
Hauptspannungszustand : Dies ist ein spezieller Zustand, bei dem die Spannungen nur entlang der Hauptachsen eines Koordinatensystems wirken. In diesem Zustand sind die Schubspannungen null.

Wir betrachten im Rahmen dieses Kurses speziell die blau gefärbten Zustände.

Einachsiger Spannungszustand

Dieser tritt in prismatischen Elementen wie Wellen, Profilen und Stäben auf. Die dabei entstehende Belastung wird dabei durch eine Grundbeanspruchungsart (Zug, Biegung,
Torsion, Schub) verursacht. Der Schnitt verläuft senkrecht zum Normalspannungsvektor. Der Spannungstensor hat bei einem einachsigen Spannungszustand die Form:

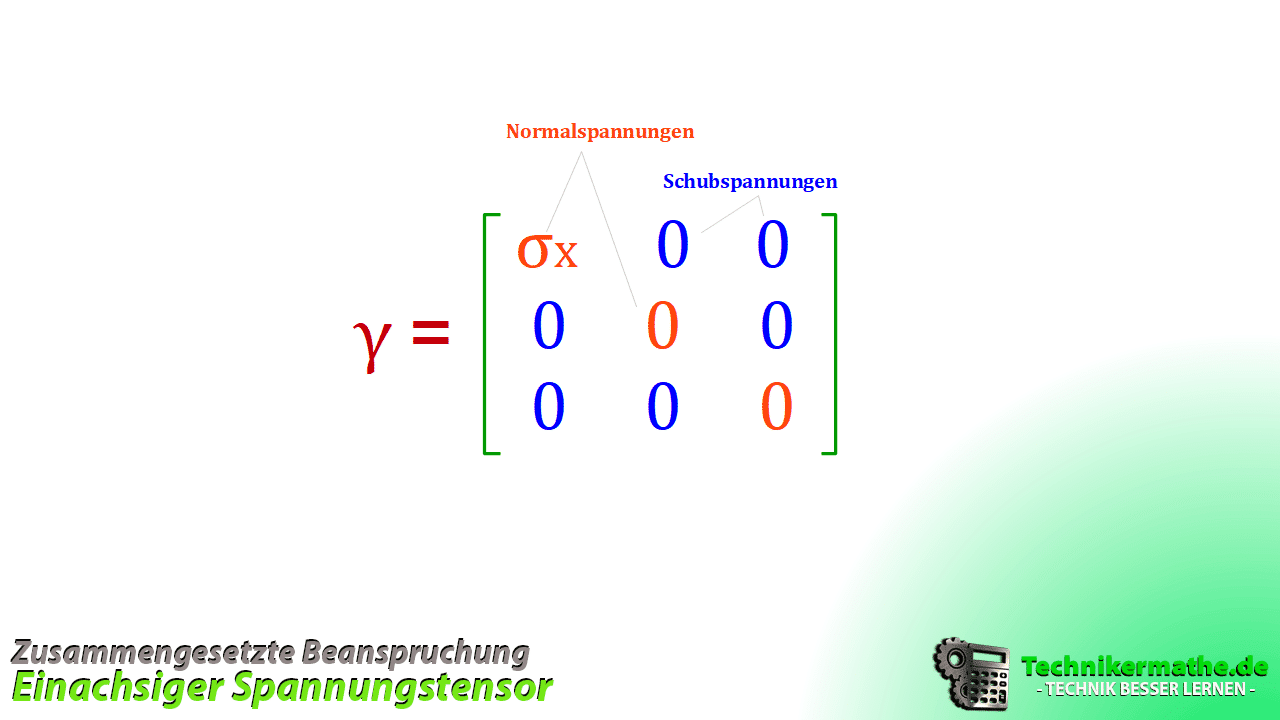
Zweiachsiger Spannungszustand

Der Zweiachsige Spannungszustand oder ebener Spannungszustand tritt hauptsächlich bei Scheiben oder dünnen Platten auf. Die Beanspruchungen wirken hierbei ausschließlich innerhalb der Scheibenebene /Plattenebene. Der Spannungstensor hat bei einem zweiachsigen Spannungszustand die Form:

Merk’s dir!

Zweiachsige Spannungszustände treten ebenfalls in prismatischen Objekten auf, insofern die gewählte Schnittebene nicht senkrecht zur Normalspannungsrichtung verläuft.

Das bedeutet: Der einachsige Spannungszustand entsteht aus dem zweiachsigen Spannungszustand durch entsprechende Wahl der Schnittlage.

Glücklicherweise sind mit dem zweiachsigen Spannungszustand die meisten Anwendungsfälle im Maschinenbau berechenbar, da im Bereich ungestörter Krafteinleitung in beinahe jedem Fall in einer Richtung die Beanspruchungen vernachlässigbar klein sind.

Räumliche Spannungszustände sind vornehmlich im Bereich der Lasteinleitung und der Kerben zu berücksichtigen. Diese sind die wesentliche Ursache für das Auftreten von dreiachsigen
Spannungszuständen.

Beispiele für Räumliche Spannungszustände!

Typische Beispiele sind
• Spannungen in Kerben mit Kraftumlenkungen und
• dickwandige Hohlzylinder mit Druckeinwirkung.

Hauptspannungszustände

Ziel der Berechnung der Hauptspannungszustände ist die Bestimmung der Beanspruchung, welche im Bauteil vorherrscht. Die Ergebnisse werden anschließend mit den Auswertungen von passenden Werkstoffversuchen [Zugversuch] verglichen. Hierzu verlagert man die gedachte Schnittebene in das Bauteil bei gegebenem Spannungszustand, so dass lediglich Normalspannungen auftreten.

Man wählt diese Vorgehensweise um einen Vergleich den Ergebnissen des Zugversuchs zu ermöglichen. Denn beim Zugversuch sind nachfolgende Eigenschaften gegeben:

Spannungszustand = einachsig
Belastung = Richtung Bauteilachse
Schnittebene = Senkrecht zur Spannungsrichtung

Vergleichsspannung

Die Vergleichsspannung wird verwendet um die Gesamtwirkung mehrerer Spannungen in einem Material oder Bauteil zu bewerten und zu vergleichen. Sie ist ein wichtiger Parameter bei der Beurteilung der Festigkeit und Sicherheit von Bauteilen, die verschiedenen Arten von Spannungen ausgesetzt sind.

Die Vergleichsspannung wird oft mit dem griechischen Buchstaben “σ_v” (Sigma sub v) dargestellt und dient dazu, die Spannungen aus verschiedenen Richtungen (z. B. Normalspannungen und Schubspannungen) in eine einzige Spannung umzuwandeln, die mit den festigkeitsbezogenen Eigenschaften des Materials verglichen werden kann.

Die allgemeine Formel zur Berechnung der Vergleichsspannung lautet:

$\sigma_v = \sigma_{von Mises} = \sqrt{ \sigma^2 + 3 \cdot \tau^2}$

$\sigma_v = \sigma_{von Mises}$ : Die Vergleichgsspannung / von-Mises-Spannung
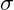$\sigma$ : Die Hauptnormalspannungen (Hauptspannungen) im Material.
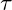$\tau$ : Die Schubspannungen (Scherspannungen) im Material.

Die Vergleichsspannung ist eine mathematische Zusammenfassung der Spannungen im Material und ermöglicht eine bessere Einschätzung der Festigkeit des Materials im Vergleich zu einer einzigen Spannungskomponente. Die Idee dahinter ist, dass das Material in einem bestimmten Spannungszustand versagt, wenn die Vergleichsspannung diesen kritischen Wert erreicht oder überschreitet.

Diese Methode bietet eine einfache Möglichkeit, die Festigkeit eines Materials oder Bauteils unter komplexen Belastungsbedingungen zu bewerten, indem sie die verschiedenen Spannungskomponenten berücksichtigt und sie in eine einzige äquivalente Spannung umwandelt.

Was kommt als Nächstes?

Nachdem wir uns mit dem Thema befasst haben, gehen wir im kommenden Kurstext auf das Thema Hypothesen ein. Darin enthalten sind: Versagenshypothesen mit Normalspannungshypothese, Schubspannungshypothese sowie Gestaltänderungshypothese.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++