[ME1] Zugbeanspruchung – Zug in der Maschinentechnik

In diesem Kurstext gehen wir auf die Zugbeanspruchung [Zug] in der Maschinentechnik näher ein. Die unterschiedlichen Beanspruchungsarten können einzeln oder in Kombination auftreten.

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Zugbeanspruchung – Definition der Zugkraft

Eine Zugbeanspruchung kann infolge der Schwerkraft (Eigengewicht) oder einer zusätzlichen Belastung durch passive Krafteinwirkung (Zusatzgewicht) oder aktiven Krafteinwirkung (Mechanik) auftreten.

Die Zugbeanspruchung kann je nach Konstruktion in jedem Winkel auf das Maschinenbauteil wirken.

Exkurs: Schwerkraft / Gewichtskraft

Die Schwerkraft, alternativ Gravitation oder Massenanziehung, ist auf der Erde annähernd konstant und wirkt vertikal zum Erdmittelpunkt.

Aufgepasst: Das betrachtete Objekt wird nicht allein von der Erde angezogen, sondern übt ebenfalls eine Anziehung auf die Erde aus.

Über die Gewichtskraft erfahren wir, wie intensiv ein Körper nach unten gezogen wird.

Gewichtskraft

Formal ermittelt sich die Kraft mit

$F_g = m \cdot g$

Kennzahlen:

$F_g =$ Gewichtskraft [in N]

$m =$ Masse [in kg]

$g =$ Ortsfaktor [in m/s²] oder [in N/kg]

Einheit Newton N – Umrechnung

$N = \frac{N}{kg} \cdot kg = \frac{kg \cdot m}{s^2}$

Die Gewichtskraft wird in Newton N angegeben. Um also einen Körper mit der Masse von 1 kg um einen m/s² zu beschleunigen, erfordert das 1 N.

Da es sich bei dem Ortsvektor g um eine Konstante (nicht veränderlich auf der Erde) handelt, hängt die Höhe der Gewichtskraft allein von der Masse m ab.

Merk’s dir!

Je mehr Masse ein Körper besitzt, umso größer ist auch seine Gewichtskraft.

Nimm es genau!

Wenn man es ganz genau nimmt, stimmt die obigen Aussage nicht. Denn die Gravitationsbeschleunigung am

Äquator bei 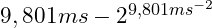$9,801 ms - 2^{9,801 ms^{-2}$ und an den
Polen bei $9,867 ms - 2^{9,867 ms^{-2}$ .

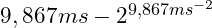$Die Masse hingegen ist überall gleich. Ein Gramm am Äquator ist auch an den Polen noch immer ein Gramm.$

$9,81 \frac{m}{s^2}$

Die Richtung, in welche die Gewichtskraft wirkt, ist immer die gleiche. Gäbe es diese Kraft insgesamt nicht, würdest du bei jedem Sprung ins Weltall aufsteigen ohne wie gewohnt wieder auf dem Boden zu landen.

Zugkraft – Anschauungsbeispiel: Aufgehängtes Rohr

In Industriehallen oder Parkgeragen finden sich beinahe immer Sprinkleranlagen. Fast das gesamte mit Wasser gefüllte Rohrsystem dafür befindet sich dicht unter der Decke, mit Stangen und Schelle angeschraubt.

Um jetzt die Beanspruchung einer Stange ermitteln zu können, müssen wir uns im Vorfeld überlegen welche Kräfte hier wirken.

Größen!

Das Gewicht des Wassers im Rohr wird mit 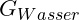$G_{Wasser}$ bezeichnet.
Das Eigengewicht des Rohrs wird mit 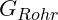$G_{Rohr}$ angegeben.
Beide Gewichte wirken vertikal nach unten [Stichwort: Gravitation]

Für ein besseres Verständnis führen wir nun einen Freischnitt durch:

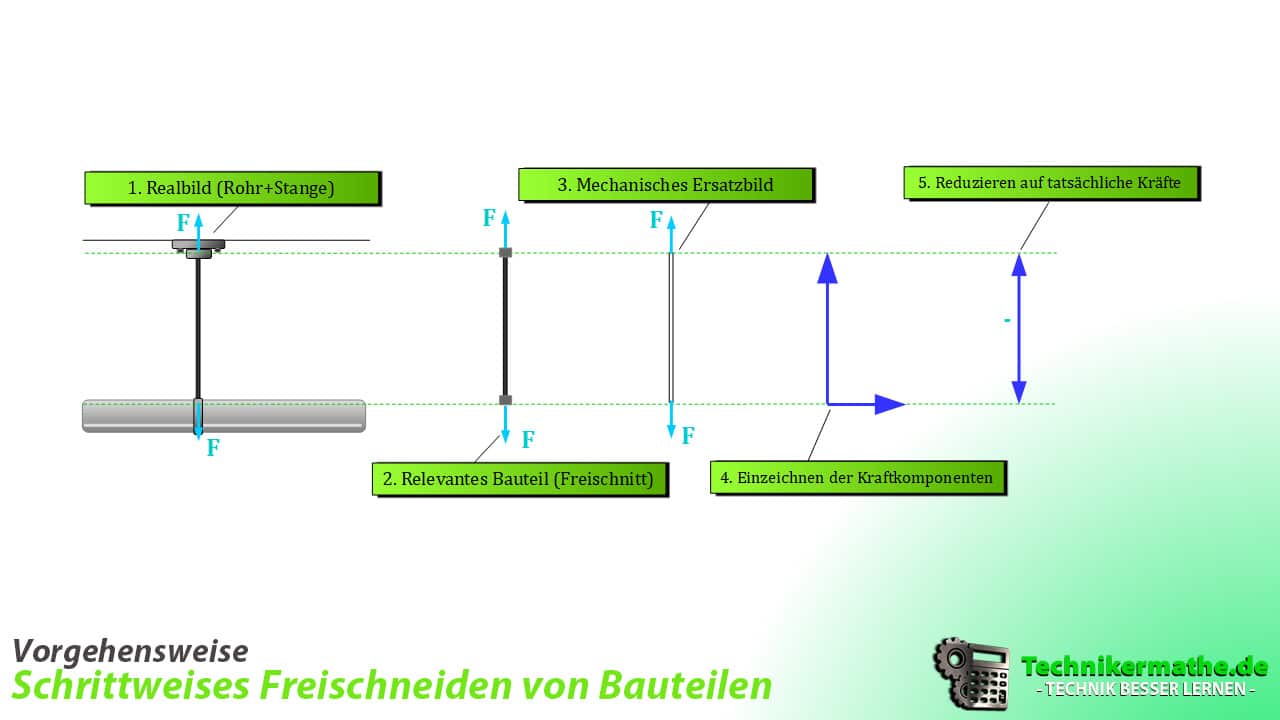
Freischneiden von Bauteilen - Zugbeanspruchung — Freischneiden von Bauteilen – Zugbeanspruchung

Jetzt haben wir einen vollständigen Freischnitt der Stange mit den wirkenden Kräften im Gleichgewicht [Gleichgewichtsbedingung].

Liegen uns die Gewichtsangaben vom Wasser und Rohr vor, so können wir die nach unten wirkende Kraft mathematisch ermitteln. Aufgrund der Gleichgewichtsbedingung können wir ebenfalls die nach oben wirkende Kraft F bestimmen. Formal sieht das dann wie folgt aus:

Gleichgewichtsbedingung

$\uparrow : F - G_{Wasser} - G_{Rohr} = 0$

Kennzahlen:

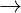$\uparrow :$ Kennzeichnung: Vertikale Gleichgewichtsbedingung [anders: $\rightarrow$ : horizontale Gleichgewichtsbedingung]
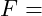$F =$ Nach oben wirkende Kraft [Haltekraft]
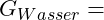$G_{Wasser} =$ Gewichtskraft des Wassers
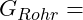$G_{Rohr} =$ Gewichtskraft des Rohrs

Merk’s dir!

Wird das Rohr zusätzlich belastet [Beispiel: Taube sitzt auf dem Rohr], so muss auch diese berücksichtigt werden [hier $G_{Taube}$ ]:

$\uparrow : F - G_{Wasser} - G_{Rohr} - G_{Taube} = 0$

Dies ist auch bei anderen Zusatzbelastungen wie Eis, Staub oder Verunreinigungen, sofern möglich, notwendig.

Zur Berechnung von $F$ lösen wir die Gleichung entsprechend auf:

Haltekraft F [aufgelöst]

$F = G_{Wasser} + G_{Rohr}$

Kennzahlen:

$\uparrow :$ Kennzeichnung: Vertikale Gleichgewichtsbedingung
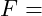$F =$ Nach oben wirkende Kraft [Haltekraft]
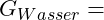$G_{Wasser} =$ Gewichtskraft des Wassers
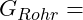$G_{Rohr} =$ Gewichtskraft des Rohrs

Die Gleichung zeigt uns erneut, dass ein Gleichgewicht zwischen der Haltekraft und den Gewichtskräften besteht. Diese wirken entgegengesetzt, sind aber betragsmäßig [ohne Vorzeichen] identisch.

Was kommt als Nächstes?

Nachdem wir uns mit der Zugbeanspruchungen befasst haben, gehen wir im nächsten Schritt über zu den Spannungen und Dehnungen die infolge von Zug auftreten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++