In diesem Kurstext gehen wir auf die Beanspruchungsart Zug in der Maschinentechnik näher ein. Wir untersuchen wie Spannungen und Dehnungen infolge einer Zugbeanspruchung auftreten.
Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.
Spannungen und Dehnungen infolge einer Zugbeanspruchung
Nachfolgend erklären wir dir getrennt voneinander, was diese beiden Größen auszeichnet und wie diese berechnet werden können.
Spannungen – Normalspannung
Liegt eine Zugbeanspruchung an einem Bauteil vor, so kommt es in dessen Inneren zur Spannungen und Dehnungen. Handelt es sich um eine reine Zugbeanspruchung so wirken nur Normalspannungen ![]() im Bauteil.
im Bauteil.
Zur Wahrung der Bauteilfestigkeit dürfen diese nicht den zulässigen Grenzwert ![]() überschreiten.
überschreiten.
Formal ermittelt man die Normalspannung mit:
![]()
Kennzahlen:
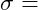 Normalspannung
Normalspannung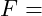 wirkende Kraft [in N]
wirkende Kraft [in N]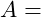 Fläche [in mm²]
Fläche [in mm²]
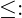 kleiner gleich
kleiner gleich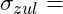 Grenzwert [maximal zulässige Spannung]
Grenzwert [maximal zulässige Spannung]
Einheit:
![]() : Kraft pro Fläche
: Kraft pro Fläche
Die Grenzwerte der Spannung für einen verwendeten Werkstoff [Material der Stange] kannst du gängigen Werkstofftabellen entnehmen.
Eine Unterschreitung der Grenzspannung sollte immer eingehalten werden, da es es sonst infolge zu starker Spannungen zum Bauteilversagen kommen kann [Überbeanspruchung].
Dehnungen
Dehnungen ![]() ebenso wie Spannungen treten infolge einer Zugbeanspruchung auf. Dass auch Wärme eine Auswirkung auf Dehnungen [Wärmedehnungen] im Material hat, lassen wir an dieser Stelle zunächst aus. Eine Dehnung ist immer dann gegeben, wenn sich die Geometrie eines Bauteils infolge von äußerer Beanspruchung verändert. Man spricht von einer relativen Längenänderung. Diese Längenänderung kann eine
ebenso wie Spannungen treten infolge einer Zugbeanspruchung auf. Dass auch Wärme eine Auswirkung auf Dehnungen [Wärmedehnungen] im Material hat, lassen wir an dieser Stelle zunächst aus. Eine Dehnung ist immer dann gegeben, wenn sich die Geometrie eines Bauteils infolge von äußerer Beanspruchung verändert. Man spricht von einer relativen Längenänderung. Diese Längenänderung kann eine
- Verlängerung [Dehnung infolge von Zugkräften]
- Verkürzung [Stauchung infolge von Druckkräften]
sein.
Formal beschreibt man die Dehnung wie folgt:
![]()
Kennzahlen:
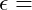 Dehnung [dimensionslos]
Dehnung [dimensionslos]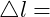 relative Längenänderung [in mm]
relative Längenänderung [in mm]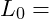 Ausgangslänge [in mm]
Ausgangslänge [in mm]
Einheit:
Die Dehnung besitzt keine Einheit – Sie ist eine Verhältniszahl. Ausgehend von der Gleichung kannst du bereits erkennen, das durch den Bruch beide einzelnen Längenangaben weggekürzt werden. Oft wird dieser Wert jedoch in Prozent angegeben.
Zugkraft – Rechenbeispiel: Kranhaken

Jetzt kommen wir zu einem Rechenbeispiel, bei welchem ein Rundprofil mit Hilfe eines Kranhakens angehoben werden soll. Als feste Verbindung zwischen Kranhaken und Profil dient ein Stab. Diese Aufgabe ist eine typische Aufgabe wie sie dir in einer Klausur begegnen könnte!
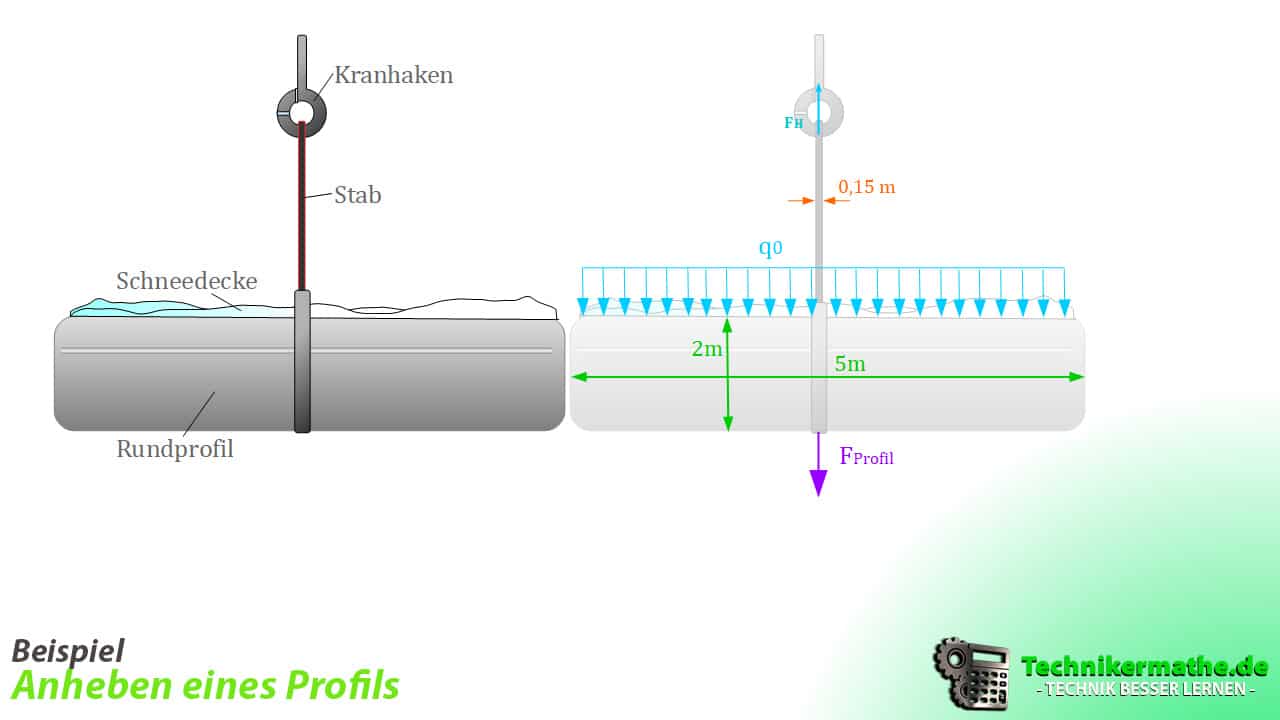
Folgende Größen sollen bestimmt werden:
- Berechne die Kraft [Haltekraft
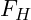 ], welche auf den Kranhaken wirkt um das Profil anzuheben.
], welche auf den Kranhaken wirkt um das Profil anzuheben. - Berechne die Spannungen
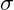 im Stab [innere].
im Stab [innere]. - Welche Dehnung
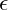 tritt im Stab auf, wenn sich dieser von 20 cm auf 24 cm verlängert.
tritt im Stab auf, wenn sich dieser von 20 cm auf 24 cm verlängert.
Gegebene Größen:
- Das Profil ist
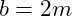 breit und
breit und 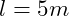 lang.
lang. - Der Stabdurchmesser (rund) beträgt
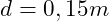
- Die durch das Profil verursachte Gewichtskraft beträgt
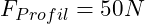
- Zudem liegt Schnee auf dem Profil [zusätzliche Flächenlast] mit
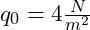
Vorgehensweise:
- Freischnitt erstellen [Darstellung zeichnerisch]
- Haltekraft am Stab berechnen [Berechnung]
- Spannungen im Stab berechnen [Schnittdarstellung +Berechnung]
- Dehnung im Stab berechnen [Berechnung]
Freischnitt erstellen
Wie gewohnt führen wir einen Freischnitt durch und reduzieren alles auf den Stab [Linie] und die daran wirkenden Kräfte:
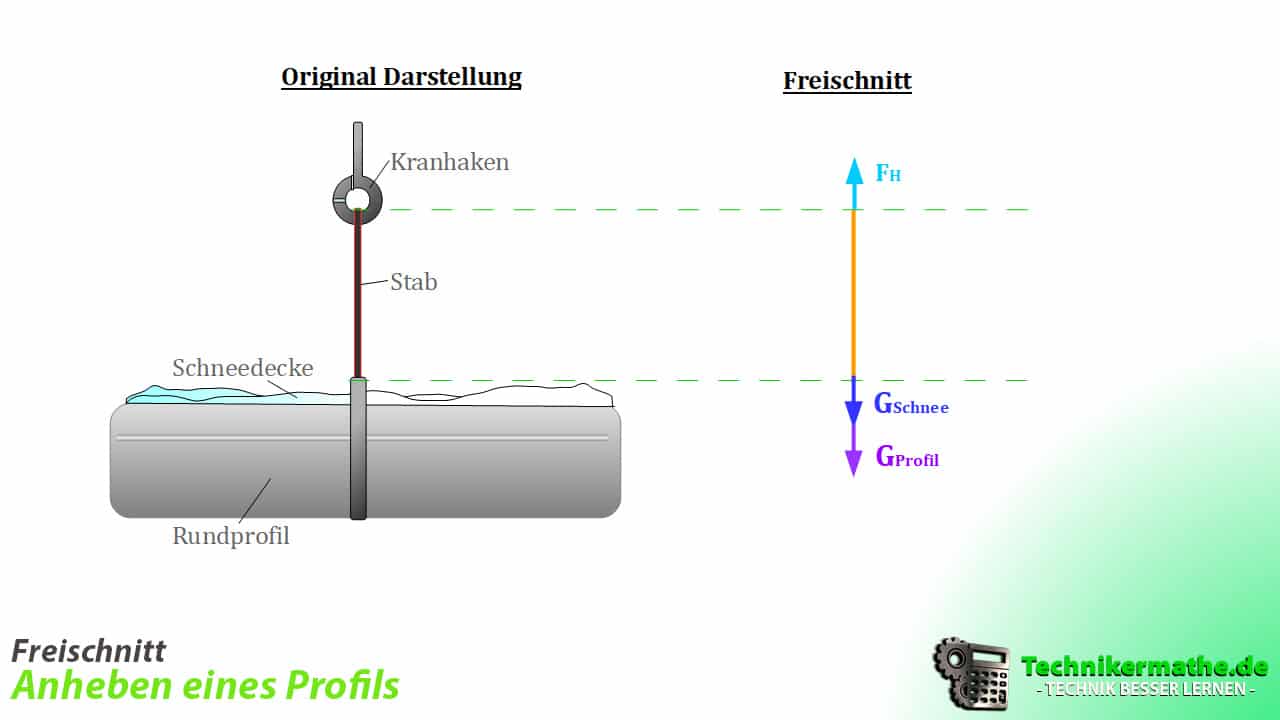
Haltekraft am Stab berechnen
Im 2. Schritt ermitteln wir die Haltekraft ![]() . Da wir bereits mit der Gewichtskraft des Profils
. Da wir bereits mit der Gewichtskraft des Profils ![]() eine der beiden notwendigen Gewichtskräfte gegeben haben, müssen wir für die vollständige Gleichgewichtsbedingung nun noch die Gewichtskraft des Schnees
eine der beiden notwendigen Gewichtskräfte gegeben haben, müssen wir für die vollständige Gleichgewichtsbedingung nun noch die Gewichtskraft des Schnees ![]() ermitteln.
ermitteln.
Ermitteln von ![]()
Diese Kraft ist eine zusammengefasste Einzellast.
Dieser Schritt gelingt uns durch Hinzunahme der Flächenlast ![]() und der Berechnung der Gesamtfläche
und der Berechnung der Gesamtfläche ![]() .
.
Unsere Ausgangsgleichung ist:
![]()
Diese Gleichung lösen wir durch Umstellen nun nach ![]() auf.
auf.
![]()
Die Angabe für ![]() haben wir bereits und setzen sie ein:
haben wir bereits und setzen sie ein:
![]()
Die Angabe für ![]() fehlt uns noch, aber wir können diese mit unseren Vorgaben errechnen:
fehlt uns noch, aber wir können diese mit unseren Vorgaben errechnen:
![]()
![]()
![]()
Zusammenrechnen und Kürzen der Flächeneinheit ergibt:
![]()
Ermitteln von ![]()
Jetzt haben wir alle notwendigen Größen um die Gleichgewichtsbedingung aufzustellen und die Haltekraft zu berechnen:
![]()
Umstellen ergibt:
![]()
Einsetzen liefert das Ergebnis:
![]()
![]()
Somit ist eine Haltekraft von 90 N notwendig um das Profil samt Schneefläche anzuheben.
Spannungen im Stab berechnen
Nachdem wir nun wissen, welche Kraft für das Anheben des Profils notwendig ist, wollen wir uns nun anschauen, welche Spannungen dadurch im Stab verursacht werden. Dieser Vorgang erlaubt es uns zu überprüfen, ob diese die zulässigen Spannungen nicht übersteigen. Lägen die auftretenden Spannungen oberhalb der zulässigen Spannungen, so würde dies zu einem Versagen des Stabe führen.
Die nachfolgende Skizze visualisiert die vorliegenden Spannungen im Zusammenhang mit den auftretenden Kräften.
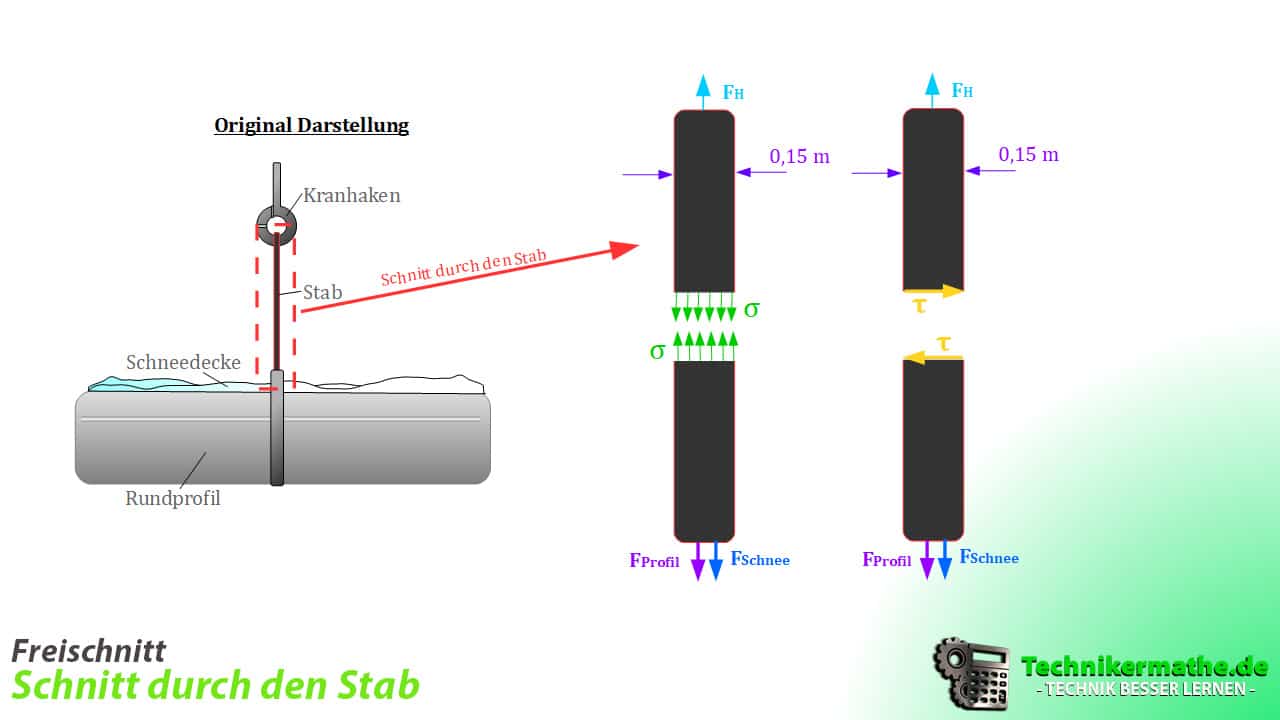
Durch den vorgenommenen Schnitt werden die Normalspannungen ![]() und die Schubspannungen
und die Schubspannungen ![]() sichtbar. Es gilt:
sichtbar. Es gilt:
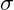 steht immer senkrecht zur Schnittfläche.
steht immer senkrecht zur Schnittfläche.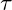 wirkt hingegen horizontal zur Schnittfläche. [Treten bei reinen Zugstäben und Druckstäben nicht auf!]
wirkt hingegen horizontal zur Schnittfläche. [Treten bei reinen Zugstäben und Druckstäben nicht auf!]
Zudem wirkt ![]() gleichmäßig verteilt auf der gesamten Schnittfläche.
gleichmäßig verteilt auf der gesamten Schnittfläche.
Formal bestimmt wird die Normalspannung mit:
![]()
Kennzahlen:
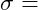 Normalspannung
Normalspannung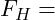 Haltekraft
Haltekraft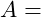 Fläche des Stabquerschnitts
Fläche des Stabquerschnitts
Zur weiteren Berechnung lösen wir die Gleichung nach ![]() auf:
auf:
![]()
Anschließend ziehen wir die vertikale Gleichgewichtsbedingung heran:
![]()
und ersetzen ![]() :
:
![]()
Als Nächstes lösen wir die gesamte Gleichung nach ![]() auf:
auf:
![]()
Jetzt benötigen wir noch die Angabe von ![]() , die sich aus unserer obigen Angabe zum Stabdurchmesser leicht errechnen lässt:
, die sich aus unserer obigen Angabe zum Stabdurchmesser leicht errechnen lässt:
![]()
![]()
![]()
Mit der Kenntnis der Kreisfläche und der beiden anderen Werte können wir jetzt die Normalspannung errechnen:
![]()
Im letzten Schritt gleichen wir unser Ergebnis mit der maximal zulässigen Spannung ab. Diese sei in unserem Fall angegeben mit:
![]()
Nach der Umrechnung auf die gleiche Einheit zeigt sich, dass der Stab die Belastung ohne Probleme aushält:
![]()
![]()
Dehnung im Stab berechnen
Im letzten Schritt möchten wir die Dehnung im Stab berechnen. Wie wir wissen beträgt die Ausgangslänge unseres Stabes ![]() und infolge der Verlängerung wird
und infolge der Verlängerung wird ![]()
Die Längenänderung ![]() lässt sich mit einfacher Subtraktion errechnen:
lässt sich mit einfacher Subtraktion errechnen:
![]()
![]()
Mit diesen Angaben können wir unter Hinzunahme der Gleichung der Dehnung, diesen Wert einfach errechnen:
![]()
![]()
![]()
Der Stab wird aufgrund der Belastung um 20 % gedehnt.
Darstellung im Spannung-Dehnungs-Diagramm
In der obigen Aufgabe haben wir mit ![]() die zulässige Spannung festgelegt. Stellt sich nun die Frage woher stammt diese Angabe?
die zulässige Spannung festgelegt. Stellt sich nun die Frage woher stammt diese Angabe?
Zuerst einmal wird jedes Material mit Hilfe des Zugversuchs hinsichtlich der zulässigen Spannung und zulässigen Dehnung geprüft. Den genauen Ablauf dafür findest du in der Lektion Zugversuch.
Mit Hilfe des Spannungs-Dehnungs-Diagramms wird mit ![]() ein Zusammenhang zwischen der Kraft
ein Zusammenhang zwischen der Kraft ![]() und der Stabverlängerung
und der Stabverlängerung ![]() hergestellt.
hergestellt.
Definitiv! Mit dem Diagramm lassen sich elastische und plastische Verformungsgrenzen festlegen, sowie Festigkeitsgrenzen und Bruchgrenzen ermitteln.
Für jede Relation erhält man ein Ergebnis. Alle Ergebnisse zusammen ergeben dann die werkstoffspezifische Kurve des Spannungs-Dehnungs-Diagramms. Nachfolgend ist dieses dargestellt:
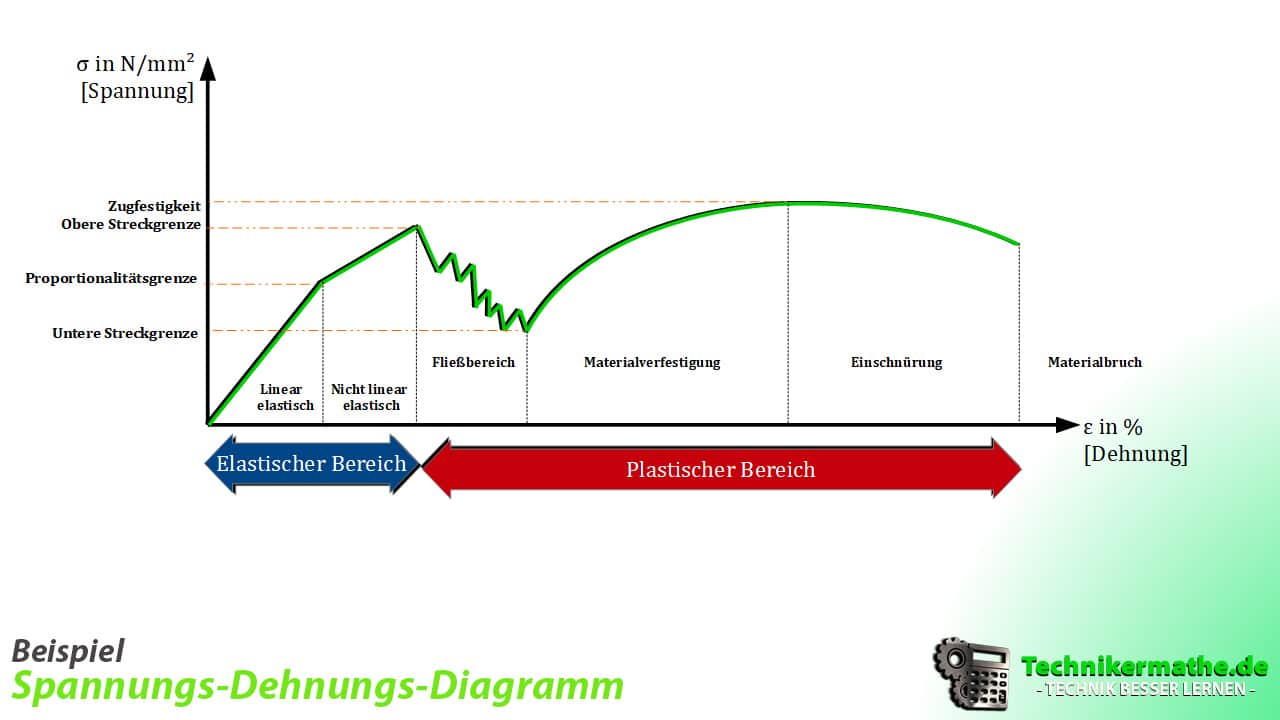
Wie du direkt erkennen kannst, unterteilt sich die Kurve in einen elastischen und einen plastischen Bereich. Zudem können 4 Grenzen ausgemacht werden:
- Dehngrenze:
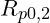 , auch technische Elastizitätsgrenze oder Proportionalitätsgrenze genannt, liegt im elastischen Bereich und besagt welche Belastung eine Dehnung von 0,2 % verursacht.
, auch technische Elastizitätsgrenze oder Proportionalitätsgrenze genannt, liegt im elastischen Bereich und besagt welche Belastung eine Dehnung von 0,2 % verursacht. - Obere Streckgrenze:
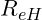 liegt auf der Grenzen vom elastischem zu plastischem Bereich und legt den Punkt fest, ab welchem eine plastische Verformung im Bauteil auftritt.
liegt auf der Grenzen vom elastischem zu plastischem Bereich und legt den Punkt fest, ab welchem eine plastische Verformung im Bauteil auftritt. - Untere Streckgrenze:
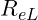 liegt im plastischen Bereich zwischen dem darin befindlichen Fließbereich und dem Bereich der Materialverfestigung. Hier kommt es zu einer Reduzierung der Spannung bei zunehmender Dehnung (Tiefpunkt).
liegt im plastischen Bereich zwischen dem darin befindlichen Fließbereich und dem Bereich der Materialverfestigung. Hier kommt es zu einer Reduzierung der Spannung bei zunehmender Dehnung (Tiefpunkt). - Zugfestigkeit:
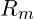 läutet das Materialversagen ein. Denn hier ist die Dehnung derart stark, dass es im weiteren Verlauf zu einem Bruch kommt.
läutet das Materialversagen ein. Denn hier ist die Dehnung derart stark, dass es im weiteren Verlauf zu einem Bruch kommt.
Nachdem wir uns mit Spannung und Dehnung bei Zug sowie dem Spannungs-Dehnungs-Diagramm befasst haben, gehen wir im nächsten Schritt über zu dem Thema Hooke’sche Gesetz und Elastizitätsmodul bei Zugkräften.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






