In diesen Kursabschnitt befassen wir uns ausführlich mit den Schubspannungen bei Biegung.
Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.
Schubspannungen bei reiner Biegung – Grundlagen
Im Gegensatz zur reinen Biegung, treten bei der Querkraftbiegung neben den Normalspannungen ![]() ebenfalls Schubspannungen
ebenfalls Schubspannungen ![]() auf. Für die Auslegung von Maschinenteilen ist immer die größte zulässige Beanspruchung interessant. Folglich interessiert uns deshalb das Widerstandsmoment.
auf. Für die Auslegung von Maschinenteilen ist immer die größte zulässige Beanspruchung interessant. Folglich interessiert uns deshalb das Widerstandsmoment.
Schubspannungen sind eine Art von Spannungen, die in einem Material auftreten, wenn Kräfte senkrecht zur Fläche des Materials angewendet werden. Sie treten auf, wenn eine Deformation oder ein Scherstress in einem Material vorhanden ist. Im Gegensatz zu normalen Spannungen, die Kräfte entlang der Fläche eines Materials darstellen, wirken Diese Spannungen parallel zur Fläche und verursachen eine Verformung durch Scherung.
Schubspannungen werden in der Regel mit dem griechischen Buchstaben “tau” (τ) bezeichnet. Sie werden in Einheiten wie Pascal (Pa) oder Newton pro Quadratmeter (N/m²) gemessen. Eine positive Spannung verursacht eine Scherung in eine Richtung, während eine negative Spannung eine Scherung in die entgegengesetzte Richtung verursacht.
Schubspannungen treten in vielen technischen Anwendungen auf, wie zum Beispiel in Tragwerken, Brücken, Fahrzeugen oder auch in der Materialbearbeitung. Sie spielen auch eine wichtige Rolle in der Festigkeitslehre, um die Scherfestigkeit eines Materials zu bestimmen.
Die Berechnung von diesen Spannungen erfolgt oft in Verbindung mit dem Schubmodul oder der Schubfestigkeit des Materials. Der Schubmodul beschreibt das Verhältnis zwischen Schubspannung und Scherdeformation. Er kann als Maß für die Fähigkeit eines Materials betrachtet werden, Scherkräfte zu widerstehen, ohne dabei plastisch zu verformen.
Schubspannungen – 4-lagiger Balken
In der nachfolgenden Abbildung entdeckst du einen 4-lagigen Balken, welcher durch eine Kraft ![]() belastet wird. Auf jeder Lage wirken in Folge der Kraft Schubspannungen.
belastet wird. Auf jeder Lage wirken in Folge der Kraft Schubspannungen.
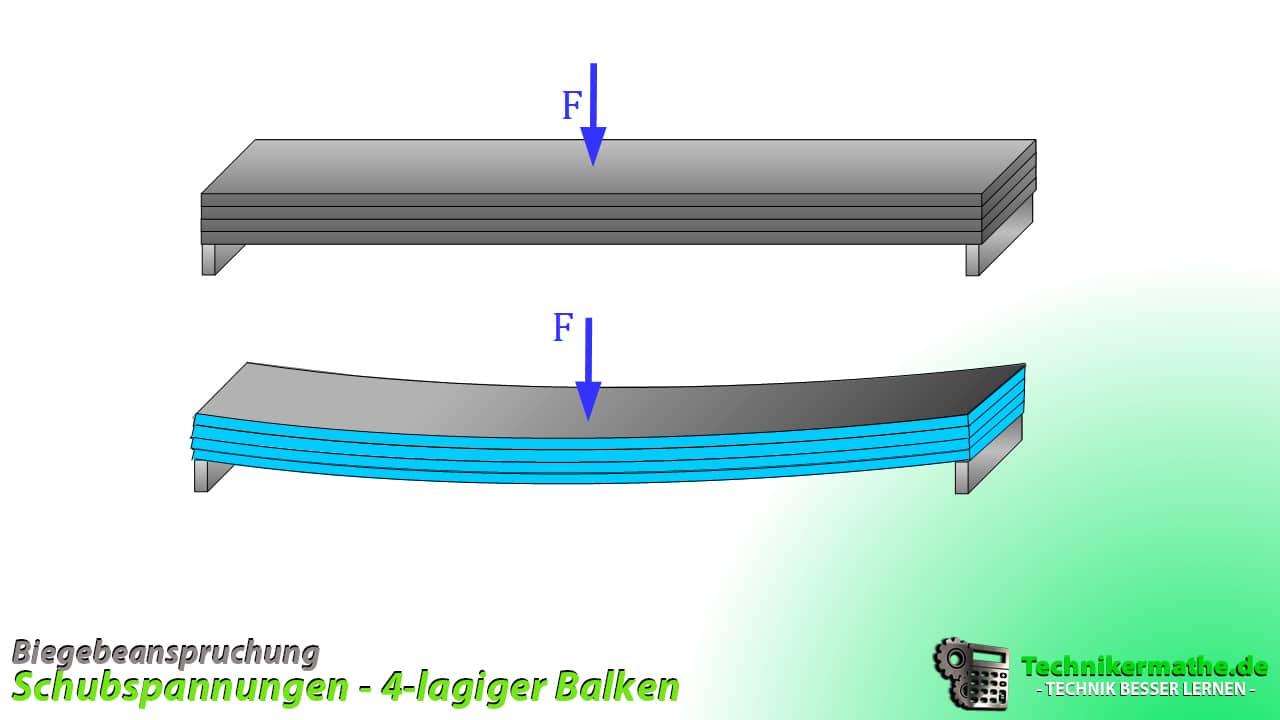
In unserem Fall sind die Spannungen derart groß, dass es zu einer Durchbiegung der einzelnen Lagen kommt.
Um dieser Durchbiegung entgegenzuwirken können Schubspannungsüberträger in die Lagen integriert werden. Hierzu können wir uns verschiedener Verbindungselemente bedienen wie
- Stiften,
- Nägel,
- Schrauben,
- Klebstoffen,
- weitere.
In der nachfolgenden Abbildung siehst du eine Lösung mit Schrauben.
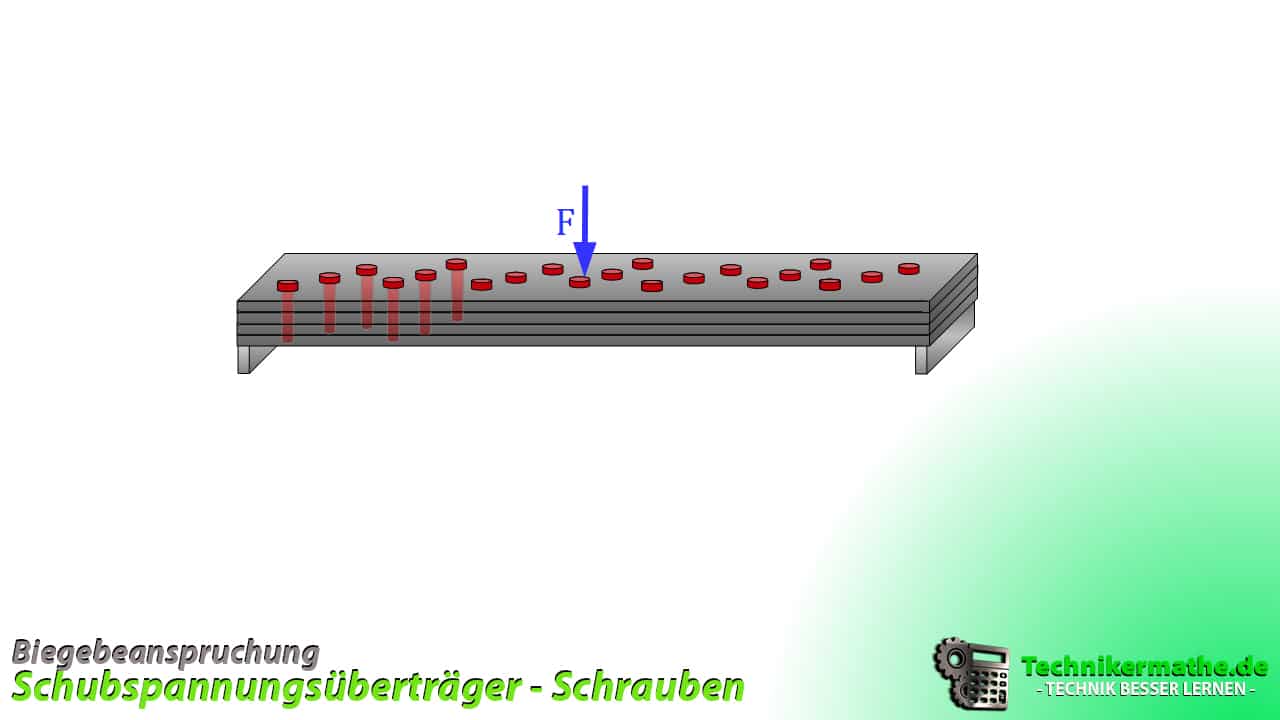
Schubspannungen bei reiner Biegung – Beispiele aus dem Alltag
Hier sind fünf weitere Beispiele aus dem Alltag, die Schubspannungen bei reiner Biegung verdeutlichen:
-
Ein Balkon: Wenn eine Person auf einem Balkon steht, der an der Hauswand befestigt ist, wirkt eine Biegekraft auf den Balkon. Dadurch entstehen Schubspannungen in den Balken oder Platten, aus denen der Balkon besteht.
-
Eine Brücke: Brücken tragen das Gewicht von Fahrzeugen, Fußgängern und anderen Lasten. Bei einer Biegung der Brücke entstehen Schubspannungen in den Trägern, Balken oder Platten, die die Brücke stützen.
-
Ein Regalbrett: Wenn Sie schwere Gegenstände auf ein Regalbrett legen, wird das Brett nach unten gebogen. Infolgedessen treten Schubspannungen im Inneren des Bretts aufgrund der relativen Verschiebung der Schichten des Materials auf.
-
Ein Tisch: Wenn sich eine Person auf einen Tisch setzt oder darauf lehnt, wird der Tisch gebogen. Dadurch entstehen Schubspannungen in den Tischbeinen oder Tischplatten.
-
Ein Fahrradlenker: Wenn Sie beim Fahrradfahren auf den Lenker drücken, um zum Beispiel Hindernissen auszuweichen, wird der Lenker gebogen. Dadurch entstehen Schubspannungen entlang des Lenkers, da sich die Ober- und Unterseite des Lenkers relativ zueinander verschieben.
Diese Beispiele verdeutlichen, wie diese Spannungen bei reiner Biegung in verschiedenen Alltagssituationen auftreten können. Es ist wichtig, die Auswirkungen dieser Spannungen auf die strukturelle Integrität der Bauteile zu berücksichtigen, um Schäden oder Versagen zu vermeiden.
Schubspannungen bei Biegung – Auswahl Profile
Nachfolgend stellen wir dir drei typische Profile aus dem Maschinenbau vor und zeigen dir zudem wie das Belastungsdiagramm sowohl die zugehörige Berechnungsgleichung aussieht:
- Vierkantprofil [mit rechteckigem Querschnitt]
- Rundprofil [mit kreisrundem Querschnitt]
- I-Profil / Doppel-T-Profil [mit doppel-T-förmigen Querschnitt]
Es muss in allen Fällen der Grundsatz gelten, dass die Querschnittsfläche ![]() konstant ist und bleibt. Das bedeutet wiederum dass immer das gleiche Gewicht pro Längeneinheit vorliegt.
konstant ist und bleibt. Das bedeutet wiederum dass immer das gleiche Gewicht pro Längeneinheit vorliegt.
Vierkantprofil
Beim Vierkantprofil sieht das Belastungsprofil je nach Anwendungszweck entweder wie ein Halbkreis (real) oder wie ein Rechteck (ideal) aus.
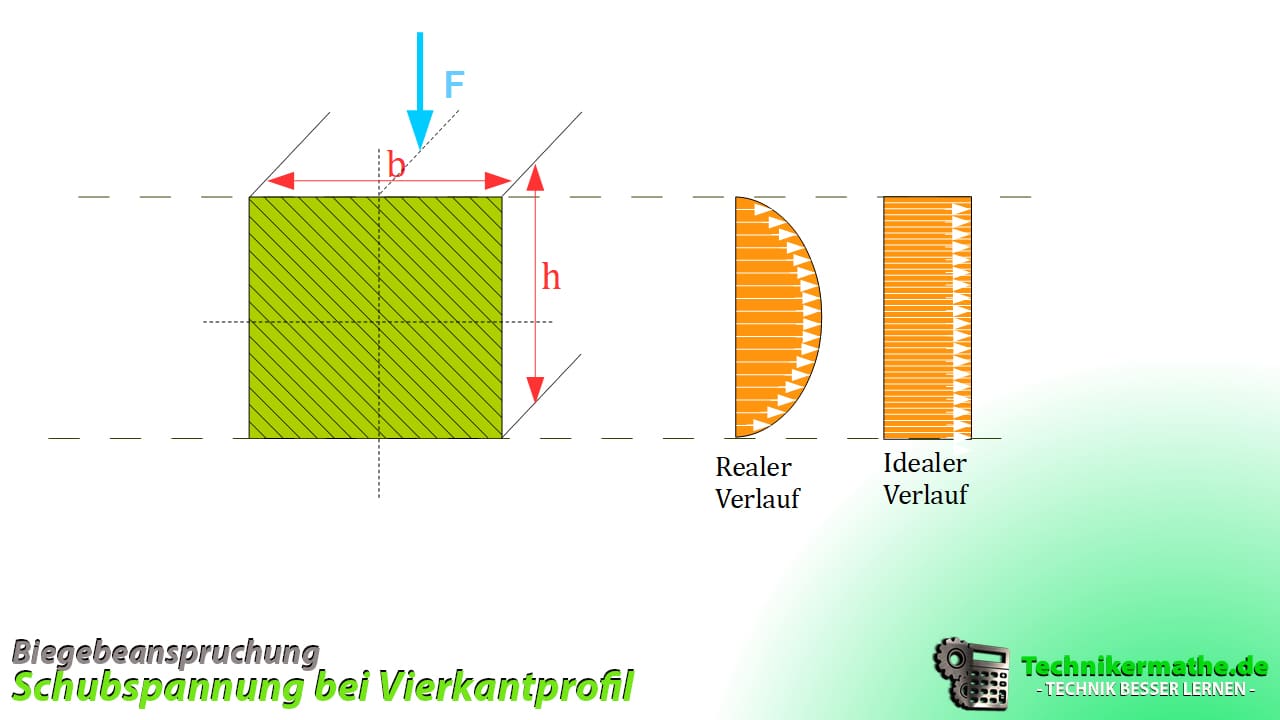
Die zugehörige Gleichung für die Berechnung der maximalen Schubspannung ist folgende:
![]()
Kennzahlen:
 Maximale Schubspannung
Maximale Schubspannung Querkraft
Querkraft Breite des Profils
Breite des Profils Höhe des Profils
Höhe des Profils
Rundprofil
Beim Rundprofil sieht das Belastungsprofil wie ein Halbkreis (real) aus.
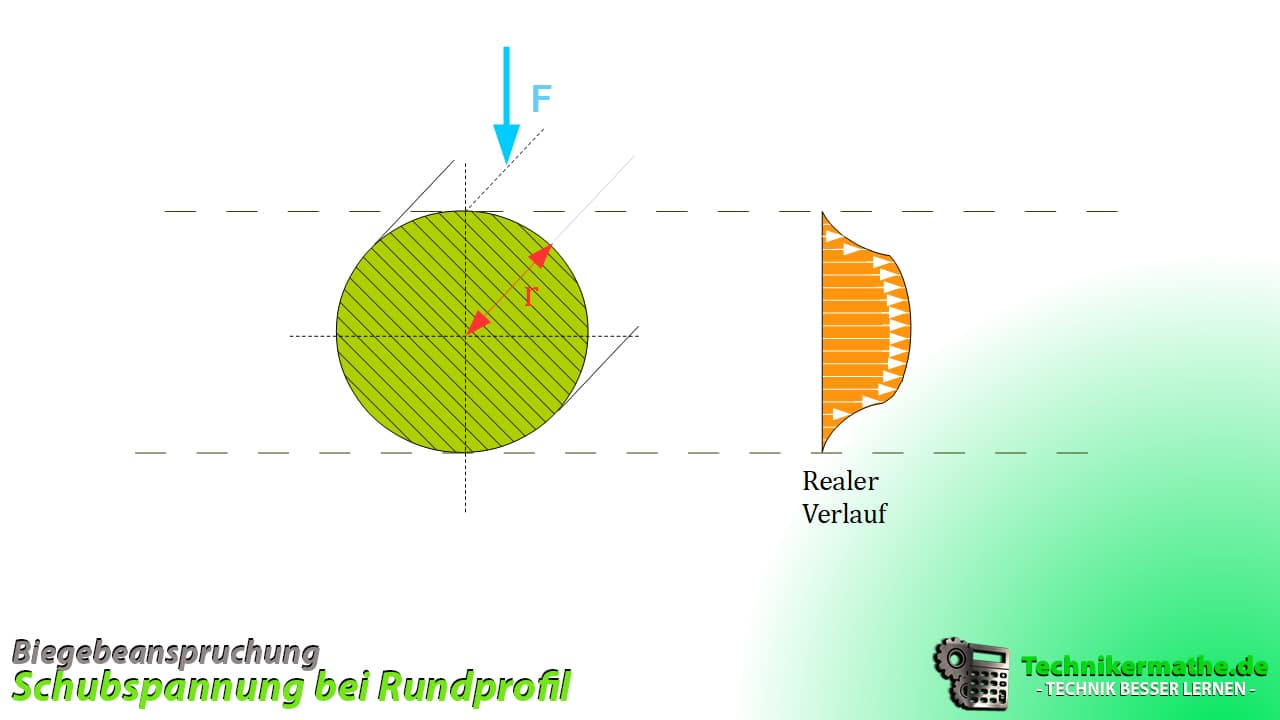
Die zugehörige Gleichung für die Berechnung der maximalen Schubspannung ist folgende:
![]()
Kennzahlen:
 Maximale Schubspannung
Maximale Schubspannung Querkraft
Querkraft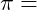 Kreiszahl
Kreiszahl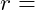 Radius
Radius
Doppel-T-Profil [I-Profil]
Beim Doppel-T-Profil sieht das Belastungsprofil wie ein Rechteck (real) aus.
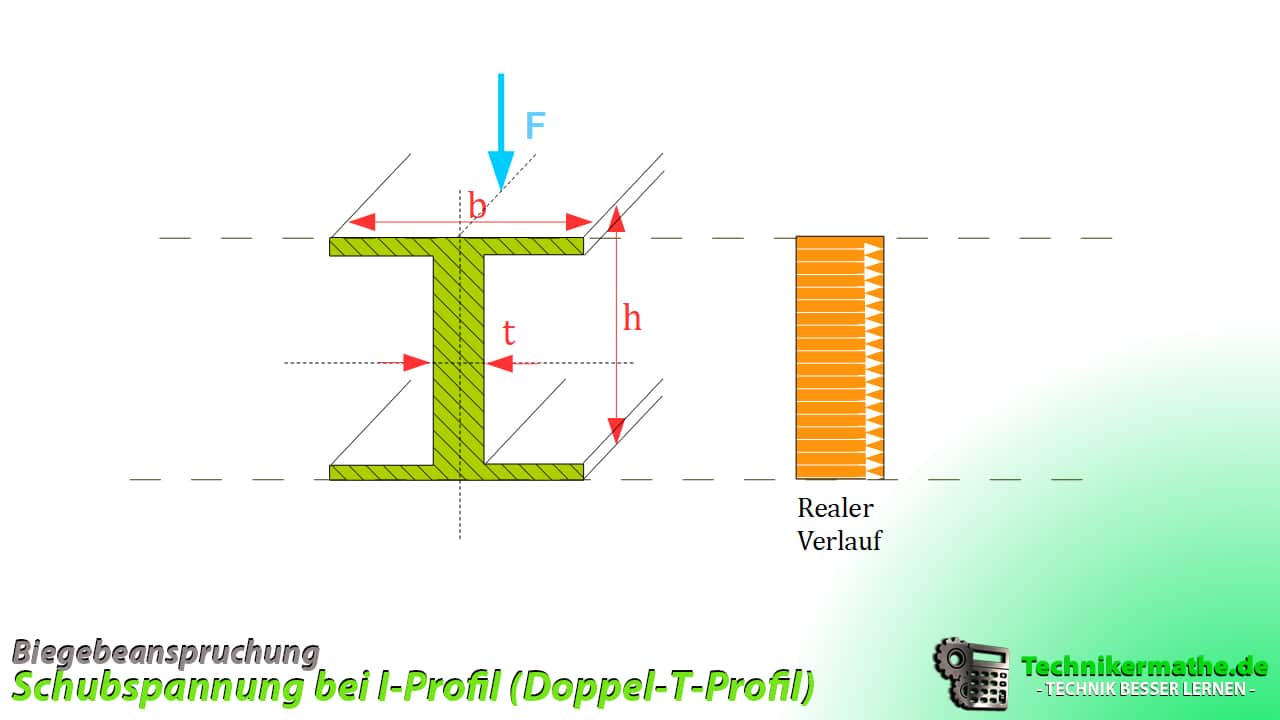
Die zugehörige Gleichung für die Berechnung der maximalen Schubspannung ist folgende:
![]()
Kennzahlen:
 Maximale Schubspannung
Maximale Schubspannung Querkraft
Querkraft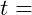 Breite des Profils (Mittelstück)
Breite des Profils (Mittelstück) Höhe des Profils
Höhe des Profils
Schubspannungen – Materialreduzierung
Sofern Material entfernt werden soll, muss darauf geachtet werden, dass der Schubverband (durch Nägel, Stifte oder Leim) erhalten bleibt. Das bedeutet, dass der Querschnitt an den Stellen der Schubübertragung nicht zu intensiv mit Löchern, Schlitzen oder anderen Schwächungen versehen werden darf.

- Die maximale Schubspannung tritt im Bereich der neutralen Faser auf. Im Bereich der Außenfaser (Maximale Normalspannung durch Biegemoment) ist die Spannung hingegen gleich Null, daher sollte hier maximal Material entfernt werden.
- Schubspannungen und Schubverformungen dürfen normalerweise für schlanke Biegeträger vernachlässigt werden. Im Bereich von kurzen Balken mit Biegebeanspruchung kann besonders die Verformung zu Problemen in der Funktionalität führen.
Schubspannungen – Scherflächen bei einer Stiftverbindung
In der nachfolgenden Abbildung siehst du zwei Rohre mit unterschiedlichem Durchmesser, die ineinander gesteckt wurden. Um diese gegen verrutschen zu sichern wurde ein Stift in beiden Rohre gesteckt (passende Bohrungen sind im Vorfeld eingebracht worden).

In unserem Fall werden nun beiden Rohre in entgegensetzte Richtung auf Zug beansprucht. Infolge der Schubspannungen ergeben sich am Bolzen (Bereich: Wandungen Innenrohr/Außenrohr) zwei Scherflächen ![]() [rote Flächen] . Sind die Zugkräfte höher als die angegebene Scherfestigkeit des Bolzens, so führt dies zu einem Abscheren an den Scherflächen
[rote Flächen] . Sind die Zugkräfte höher als die angegebene Scherfestigkeit des Bolzens, so führt dies zu einem Abscheren an den Scherflächen ![]() .
.
Mittlere Schubspannung – Formel
Für Mitnehmerteile wie Bolzen, Stifte oder weitere berechnet man die mittlere Schubspannung und gleicht diese anschließend mit der vorgegebenen Scherfestigkeit des Werkstoffs.
Formal errechnet sich das wie folgt:
![]()
Kennzahlen
 Schubspannung
Schubspannung zulässige Schubspannung
zulässige Schubspannung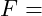 Kraft
Kraft Scherfläche
Scherfläche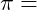 Kreiszahl
Kreiszahl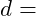 Durchmesser
Durchmesser
Die Angabe erfolgt in ![]()
Nachdem wir uns mit der zweiten Form der Spannungen bei Biegung befasst haben, gehen wir im kommenden Kurstext auf die Torsion als Form der Beanspruchung ein.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






