In diesen Kursabschnitt befassen wir uns ausführlich mit dem Thema Kerben bei einer Getriebewelle. Dabei gehen wir in dieser Prüfungsaufgabe auf die Berechnung der Beanspruchungen, Vergleichsspannungen, Werkstoffgrenzwerte & Ausnutzung im Detail ein.
Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.
Getriebewelle – Grundlagen
Eine Getriebewelle ist ein wichtiges Bauteil in einem Getriebe, das dazu dient, Drehbewegungen zwischen verschiedenen Teilen des Getriebes zu übertragen. Sie besteht in der Regel aus einer länglichen, zylinderförmigen Stange oder Welle, die typischerweise an beiden Enden Lager oder andere Verbindungselemente aufweist. Die Getriebewelle kann verschiedene Formen und Größen haben, abhängig von der Art des Getriebes und seiner Anwendung.

Die Hauptfunktion einer Getriebewelle besteht darin, die Energie und das Drehmoment von der Eingangswelle (z. B. von einem Motor) auf die Ausgangswelle (die die Antriebskraft an die Räder oder andere Teile des Fahrzeugs überträgt) zu übertragen.
Dies geschieht oft durch eine Reihe von
- Zahnrädern,
- Kupplungen und
- anderen Mechanismen,
die auf der Getriebewelle angebracht sind.
Die Getriebewelle spielt somit eine zentrale Rolle bei der Steuerung und Anpassung der Geschwindigkeit und des Drehmoments in einem Fahrzeug oder einer Maschine, um die gewünschte Leistung und Fahrzeugbewegung zu erreichen.
Getriebewelle mit Kerbe – Ausgangssituation
Eine Getriebewelle mit Kerbe ist eine Getriebewelle, die eine oder mehrere Nuten oder Kerben auf ihrer Oberfläche aufweist. Diese Kerben dienen dazu, verschiedene Komponenten wie Ringe, Buchsen, Lager oder Riemenscheiben sicher auf der Welle zu fixieren. Die Kerben bieten eine Art Verriegelung oder Haltemechanismus, der verhindert, dass die auf der Welle montierten Teile während des Betriebs verrutschen oder sich lösen.
![Getriebewelle mit Kerbe [Variante 2]](https://technikermathe.de/wp-content/uploads/2023/11/Getriebewelle-mit-Kerbe-2.jpg)
Die Anzahl und Position der Kerben auf der Getriebewelle hängen von der spezifischen Anwendung und dem Design des Getriebes ab. Sie werden oft in einem bestimmten Muster angebracht, um eine sichere Verbindung und Positionierung der Komponenten zu gewährleisten.
Getriebewellen mit Kerben sind weit verbreitet in verschiedenen mechanischen Systemen, insbesondere in Getrieben, die in Fahrzeugen, Maschinen und anderen Geräten eingesetzt werden.
Geplante Kerben tragen dazu bei, die Funktionalität und Zuverlässigkeit des Getriebes zu verbessern, indem sie die ordnungsgemäße Positionierung der Komponenten sicherstellen.
Getriebewelle mit Kerbe – Prüfungsaufgabe
Wie du bereits erfahren hast, weist eine Getriebewelle in den meisten Fälle gleich mehrere Kerben auf, weshalb wir nun für ein besseres Verständnis eine Festigkeitsberechnung als Festigkeitsnachweis durchführen werden.
Nachfolgend siehst du den Ausschnitt einer Getriebewelle, welcher uns als Berechnungsgrundlage dient.
![Getriebewelle mit Kerbe [Ausschnitt / Schema]](https://technikermathe.de/wp-content/uploads/2023/11/Getriebewelle-mit-Kerbe-3.jpg)
Du kannst der Abbildung entnehmen, dass die Welle eine Kerbe mit dem Durchmesser ![]() und einem Kerbradius
und einem Kerbradius ![]() aufweist und durch eine Zugbeanspruchung
aufweist und durch eine Zugbeanspruchung ![]() , ein Biegemoment
, ein Biegemoment ![]() sowie ein Torsionsmoment
sowie ein Torsionsmoment ![]() belastet wird.
belastet wird.
Getriebewelle – Aufgabenstellung
Nun verschaffen wir uns einen Überblick zu den gesuchten Größen, sowie für gegebenen Größen, die eine Berechnung erst ermöglichen.
Gesuchte Größen:
Es sollen im Rahmen des Festigkeitsnachweises folgende Größen berechnet werden:
Beanspruchungen:
![]() Zugbeanspruchung,
Zugbeanspruchung,
![]() Biegemoment,
Biegemoment,
![]() Torsionsmoment
Torsionsmoment
Vergleichsspannungen:
![]() Mittelspannung,
Mittelspannung,
![]() Ausschlagspannung,
Ausschlagspannung,
![]() Vergleichsspannung mit statischem & dynamischen Anteil
Vergleichsspannung mit statischem & dynamischen Anteil
Werkstoffgrenzwert:
![]() Werkstoffgrenzwert
Werkstoffgrenzwert
Ausnutzung:
![]() Ausnutzung
Ausnutzung
Angaben: Gegebene Größen
Um erfolgreiche Berechnungen durchführen zu können, benötigen wir selbstverständlich einige Angaben, ohne welche ein Festigkeitsnachweis nicht durchgeführt werden kann.
Belastungsangaben:
- Zugbelastung:

- Biegemoment:

- Torsionsmoment:

Sicherheitsfaktor gegen Bruch (Wellenversagen): ![]() [dimensionlose Zahl]
[dimensionlose Zahl]
Kerbangaben:
- Querschnitt der Kerbe:

- Radius der Kerben:

- Dimensionslose Kerbformzahl für Zug:

- Dimensionslose Kerbformzahl für Biegung:

- Dimensionslose Kerbformzahl für Zug:

Die Kerbformzahlen, können für die unterschiedlichen Belastungsfälle aus Tabellenbüchern entnommen werden.
Werkstoffangaben:
- Bezeichnung [Werkstoffnummer] : 16MnCr5 [Alt: EC80] [Werkstoffnummer: 1.7132]
- Zugfestigkeit:

- Streckgrenze:

Der Werkstoff 1.7131 bzw. 16MnCr5, der auch heute noch unter seiner alten Bezeichnung EC80 bekannt ist, ist ein chrom-manganlegierter Einsatzstahl nach EN 10084 mit einer maximal zu erreichenden Lieferhärte von 207 HB. Verwendet wird dieser Stahl vor allem für verschleißbeanspruchte Bauteile, die über eine hohe Festig- sowie Zähigkeit und eine Kernfestigkeit von 800 bis 1100 N/mm2 verfügen müssen.
Getriebewelle – Lösung
Die Kenntnis der obigen Angaben / Größen, erlaubt uns nun eine Berechnung durchzuführen.
Beanspruchungen
Wir beginnen mit den Beanspruchungen sowie der Ermittlung der maximal, zulässigen Werte.
Zugbeanspruchung
Eine Zugbeanspruchung wird im Normalfall mit nachfolgender Gleichung bestimmt:
![]()
Kennzahlen:
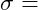 Zugbeanspruchung
Zugbeanspruchung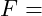 Kraft
Kraft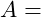 Querschnittsfläche
Querschnittsfläche
Die Fläche bei einem Kreisquerschnitt berechnet sich wie folgt:
![]()
Kennzahlen
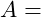 Kreisfläche
Kreisfläche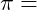 Kreiszahl [3.14159….]
Kreiszahl [3.14159….]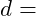 Durchmesser
Durchmesser
Mit unseren Angaben folgt daraus:
Wir setzen die Flächengleichung in die allgemeine Gleichung ein, wodurch die Zahl 4 in den Zähler hochrutscht [Kehrwert] und Kreiszahl & Durchmesser² im Zähler verbleiben.
![]()
Jetzt setzen wir die Werte ein:
![]()
Ausgerechnet erhalten wir als Ergebnis:
![]()
Um diese Größe zu ermitteln, multiplizieren wir unser obiges Ergebnis mit der Kerbformzahl für Zug:
![]()
Einsetzen der Werte:
![]()
Als Ergebnis erhalten wir:
![]()
Biegebeanspruchung
Eine Biegespannung wird mit der nachfolgenden Gleichung bestimmt:
![]()
Kennzahlen:
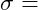 Biegespannung
Biegespannung Biegemoment
Biegemoment Widerstandsmoment [Abhängig von der Geometrie]
Widerstandsmoment [Abhängig von der Geometrie]
Das Widerstandsmoment für einen runden Balken [Getriebewelle] wird angegeben mit ![]()
![]()
Einsetzen der bekannten Werte ergibt:
![]()
Wir erhalten als Ergebnis:
![]()
Um diese Größe zu ermitteln, multiplizieren wir unser obiges Ergebnis mit der Kerbformzahl für Biegung:
![]()
Einsetzen der Werte:
![]()
Als Ergebnis erhalten wir:
![]()
Torsionsbeanspruchung
Eine Scherung wird mit der nachfolgenden Gleichung bestimmt:
![]()
Kennzahlen:
 Scherung
Scherung Scherungsmoment
Scherungsmoment plastisches Widerstandsmoment [Abhängig von der Geometrie]
plastisches Widerstandsmoment [Abhängig von der Geometrie]
Das plastische Widerstandsmoment für einen runden Balken [Getriebewelle] wird angegeben mit ![]()
![]()
Einsetzen der bekannten Werte ergibt:
![]()
Wir erhalten als Ergebnis:
![]()
Um diese Größe zu ermitteln, multiplizieren wir unser obiges Ergebnis mit der Kerbformzahl für Scherung (Torsion):
![]()
Einsetzen der Werte:
![]()
Als Ergebnis erhalten wir:
![]()
Vergleichsspannungen
Mit der Kenntnis der notwendigen Spannungen von Zug, Biegung & Torsion, gehen wir jetzt einen Schritt weiter und ermitteln die Vergleichsspannung. Hierzu benötigen wir Kenntnis darüber welche Arten von Lastfällen auftreten. Bei der Mittelspannung und Ausschlagspannung gilt folgendes:
Mittelspannungen
Dass es sich hier um die Mittelspannungen handelt, erkennst du am tiefergestellten m.
Ausschlagspannungen
Gestaltänderungsenergiehypothese
Für das weitere Vorgehen benötigen wir diese Hypothese. Wobei es sich in unserem Fall um einen fließfähigen Werkstoff handelt, bei welchem im statischen Anteil der Vergleichsspannung die Kerbwirkung unberücksichtigt bleibt. Die Kerbformzahlen sind dann ![]()
Für die Mittelspannung gilt dann:
![]()
Nun setzen wir die bekannten Werte ein:
![]()
Als Ergebnis erhalten wir:
![]()
Hier müssen wir nach Bollenrath-Troost berücksichtigen: ![]() aufgelöst nach
aufgelöst nach ![]() erhalten wir:
erhalten wir: ![]()
Für die Ausschlagspannung gilt dann:
![]()
Nun die bekannten Werte einsetzen:
![]()
Als Ergebnis erhalten wir:
![]()
Vergleichsspannung
Jetzt sind wir am Ziel und haben alle Werte um die Vergleichsspannung zu ermitteln, die sich aus einem statischen (Mittelspannung) und einem dynamischen (Ausschlagspannung) Anteil zusammensetzt.
![]()
Formal ist das:
![]()
Einsetzen der Werte:
![]()
Als Ergebnisse erhalten wir:
![]()
sowie
![]()
Werkstoffgrenzwerte
Zur Bestimmung des Werkstoffgrenzwertes können wir das zugehörige Smith-Diagramm [Werkstoff: EC80] heranziehen und direkt aus diesem ablesen. Es ergeben sich insgesamt 3 Kurven, je eine pro Belastungsart.
 Biegedauerfestigkeit
Biegedauerfestigkeit Zugdauerfestigkeit, Druckdauerfestigkeit
Zugdauerfestigkeit, Druckdauerfestigkeit Torsionsdauerfestigkeit
Torsionsdauerfestigkeit
![Smith-Diagramm, [Werkstoff 16MnCr5]](https://technikermathe.de/wp-content/uploads/2023/11/Getriebewelle-mit-Kerbe-4.jpg)
Aus dem Diagramm können wir ablesen, dass der Grenzwert für eine Zug- oder Druckbeanspruchung bei ![]() liegt.
liegt.
Der oben abgelesene Werkstoffgrenzwert für Zug oder Druck ändert sich je nach Werkstückdurchmesser.
Für das weitere Vorgehen ziehen wir den ermittelten Wert für die Mittelspannung ![]() heran. Diesen Punkt suchen wir jetzt auf der Gerade im Smith-Diagramm. Hierzu bewegen wir uns an der entsprechenden Position auf der x-Achse des Diagramms vertikal nach oben, bis zu der Stelle wo die Gerade für die Zugdauerfestigkeit geschnitten wird. In diesem Schnittpunkt erhalten wir für die Mittelspannung von
heran. Diesen Punkt suchen wir jetzt auf der Gerade im Smith-Diagramm. Hierzu bewegen wir uns an der entsprechenden Position auf der x-Achse des Diagramms vertikal nach oben, bis zu der Stelle wo die Gerade für die Zugdauerfestigkeit geschnitten wird. In diesem Schnittpunkt erhalten wir für die Mittelspannung von ![]() für die Grenzspannung einen Wert von
für die Grenzspannung einen Wert von ![]() .
.
Zur Formulierung der Gleichung für ![]() benötigen wir 3 Größen
benötigen wir 3 Größen
- Vergleichsspannung:

- Grenzspannung:

- Sicherheit gegen Bruch:
 [
[ = griechischer Buchstabe NÜ ]
= griechischer Buchstabe NÜ ]
![]()
Einsetzen der Werte
![]()
Als Ergebnis erhalten wir
![]()
Ausnutzung
Im letzten Schritt bestimmen wir die Ausnutzung ![]() . Diese errechnet sich mit der nachfolgenden Gleichung.
. Diese errechnet sich mit der nachfolgenden Gleichung.
![]()
Einsetzen der Werte ergibt:

Als Ergebnis erhalten wir:
![]()
Wir haben eine Ausnutzung von 45 % gegeben.
Mit dieser Teilberechnung der Ausnutzung schließen wir unseren Festigkeitsnachweis ab. Wir stellen fest, dass unter den gegebenen Umständen, die Getriebewelle mit Kerbe hält.
Nachdem wir uns mit dem Thema befasst haben, gehen wir im kommenden Kursabschnitt intensiv auf das Thema Korrosion ein.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






