[ME1] Normalspannungen bei Biegung

In diesen Kursabschnitt befassen wir uns ausführlich mit den Normalspannungen bei Biegung.

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Normalspannungen bei reiner Biegung

Normalspannungen bei Biegung: Ausgangssituation

Nachdem wir bereits auf die Biegebeanspruchung im allgemeinen eingegangen sind, folgt nun die Ermittlung und Berechnung der Normalspannungen bei Biegung. Dazu erinnern wir uns an:

Merk’s dir!

Wichtige Annahmen:

Beanspruchungen: Dem äußeren Moment stehen innere Spannungen gegenüber, welche

nach Bernoulli: Querschnitte bleiben eben! [Für linearen Verformungszustand erforderlich]
nach St. Vernant: Ausreichender Abstand zwischen Einspannung und Angriffsstelle [Verhältnis | Dimensionierung des Balkens ( Länge zu Höhe: 5 : 1) $l \le 5 \cdot h$ ]

über die Querschnittsfläche des Balkens als linear verteilt angenommen werden.

Normalspannungen bei reiner Biegung: Erklärung

Wird ein Balken oder eine Platte gebogen, so treten Normalspannungen auf. Normalspannungen sind die Spannungen, die immer senkrecht zur Oberfläche des Bauteils wirken.

Was ist da los…

Bei der Biegung wird ein Balken oder eine Platte einer Biegebelastung ausgesetzt, die zu einer Krümmung oder Verformung führt. Dabei treten auf der Oberseite des Balkens Druckspannungen und auf der Unterseite Zugspannungen auf.

Beispiel!

Schauen wir uns hierzu eine einfache Abbildung an:

Reine Biegung, Normalspannungen, Druckspannungen, Zugspannungen

Wie du der Abbildung entnehmen kannst, werden an den Rändern des Balkens zwei Biegemomente aufgebracht.

Dabei tritt die maximale Druckspannung an der Oberseite des Balkens auf, in dem Bereich, der am weitesten von der neutralen Faser entfernt ist.

Die maximale Zugspannung tritt dagegen an der Unterseite des Balkens auf, ebenfalls in dem Bereich, der am weitesten von der neutralen Faser entfernt ist.

Im Bereich der neutralen Faser tritt hingegen keine Spannung auf.

Die Größe der Normalspannungen hängt von vielen unterschiedlichen Faktoren ab, darunter

die angewendete Biegekraft,
die Geometrie des Balkens oder der Platte und
die Materialeigenschaften wie die Zugfestigkeit und die Druckfestigkeit.

Die Normalspannungen können mit Hilfe der Biegetheorie berechnet werden.

Biegetheorie?…

Die Biegetheorie betrachtet den Balken oder die Platte als eindimensionalen Körper, der einer Biegebelastung ausgesetzt ist. Unter Verwendung von Gleichungen wie der Biegegleichung und dem Spannung-Dehnungs-Diagramm des Materials kann man die Normalspannungen in Abhängigkeit von der Position auf dem Balken oder der Platte bestimmen.

Es ist wichtig zu beachten, dass bei der Biegung auch Schubspannungen auftreten können, die parallel zur Oberfläche des Materials wirken. Diese Schubspannungen spielen ebenfalls eine Rolle bei der Gesamtbelastung des Balkens oder der Platte, werden jedoch in der Erklärung der Normalspannungen nicht berücksichtigt.

Normalspannungen – Spannungsverlauf

In der nachfolgenden Abbildung siehst du den Verlauf der Normalspannungen bei reiner Biegung mit positivem Biegemoment:

Balkenausschnitt - Spannungsverlauf (Dehnung, Stauchung) — Balkenausschnitt – Spannungsverlauf (Dehnung, Stauchung)

Wie du der Abbildung deutlich entnehmen kannst, ist, dort wo der Abstand zur neutralen Faser (Balkenmitte / Schwerpunkt) am größten ist das Spannungsminimum $\sigma_{max}$ (Balkenoberseite) und das Spannungsmaximum $\sigma_{min}$ (Balkenunterseite). Somit liegen die maximalen und minimalen Werte (maximale Stauchung und maximale Dehnung) an den Rändern.

Normalspannungen – Formeln

Nachfolgenden betrachten wir die notwendigen Gleichung bei einer reinen Biegung:

Spannung bei reiner Biegung

$\sigma_x (z) = \frac{M_b}{I_y} \cdot d$

Kennzahlen:

$\sigma_x (z) =$ Spannung
$M_b =$ Biegemoment
$I_y =$ Flächenträgheitsmoment vom Querschnitt
$d =$ Abstand zur neutralen Faser

Ausgehend von dieser allgemeinen Gleichung, formulieren wir diese entsprechend für die Bauteiloberseite und Bauteilunterseite um:

Maximale Spannung bei reiner Biegung (Bauteilunterseite)

$\sigma_{x; max} = \frac{M_b}{I_y} \cdot d_1$

Kennzahlen:

$\sigma_{x; max} =$ maximale Spannung
$M_b =$ Biegemoment
$I_y =$ Flächenträgheitsmoment vom Querschnitt
$d_1 =$ Abstand zur neutralen Faser (Unterseite)

Minimale Spannung bei reiner Biegung (Bauteiloberseite)

$\sigma_{x; min} = \frac{M_b}{I_y} \cdot d_2$

Kennzahlen:

$\sigma_{x; min} =$ minimale Spannung
$M_b =$ Biegemoment
$I_y =$ Flächenträgheitsmoment vom Querschnitt
$d_2 =$ Abstand zur neutralen Faser (Oberseite)

Widerstandsmoment bei reiner Biegung

Widerstandsmoment – Erklärung

Merk’s dir!

Das Widerstandsmoment $W_b$ in der reinen Biegung ist ein Begriff aus der Festigkeitslehre und beschreibt die Fähigkeit eines Bauteils, Biegebelastungen zu widerstehen. Es spielt eine wichtige Rolle bei der Berechnung der Beanspruchung und Dimensionierung von Trägern, Balken und anderen Bauteilen, die Biegebelastungen ausgesetzt sind.

Das Widerstandsmoment wird üblicherweise mit dem Symbol “W” oder “I” bezeichnet und hängt von der Geometrie des Bauteils ab. Es wird in der Regel für Querschnittsformen verwendet, die eine bestimmte Symmetrie aufweisen, wie zum Beispiel

rechteckige,
runde oder
I-förmige

Querschnitte.

Das Widerstandsmoment misst die Verteilung des Materials im Querschnitt und beeinflusst die Steifigkeit und Festigkeit des Bauteils gegenüber Biegebelastungen. Je größer das Widerstandsmoment ist, desto widerstandsfähiger ist das Bauteil gegen Biegebeanspruchung.

Einfach gesprochen ist es eine Kennzahl dafür, welchen Widerstand ein Balken bei einer Belastung den entstehenden, inneren Spannungen entgegenzusetzen vermag.

Widerstandsmoment – Formel

Das Widerstandsmoment setzt das Flächenträgheitsmoment $I$ ins Verhältnis zum maximalen senkrechten Abstand $d_{max}$ zur neutralen Faser. Dort an der Randfaser liegt die maximale Beanspruchung des Bauteils vor.

Widerstandsmoment

$W_b = \frac{I_y}{d_{max}}$

Kennzahlen:

$W_b =$ Widerstandsmoment
$I_y =$ Flächenträgheitsmoment vom Querschnitt
$d_{max} =$ maximaler Abstand zur neutralen Faser

Widerstandsmomente für ausgewählte Balkenprofile

In der nachfolgenden Abbildung siehst du einige Balkenprofile gelistet nach steigendem Widerstandsmoment $W_b$

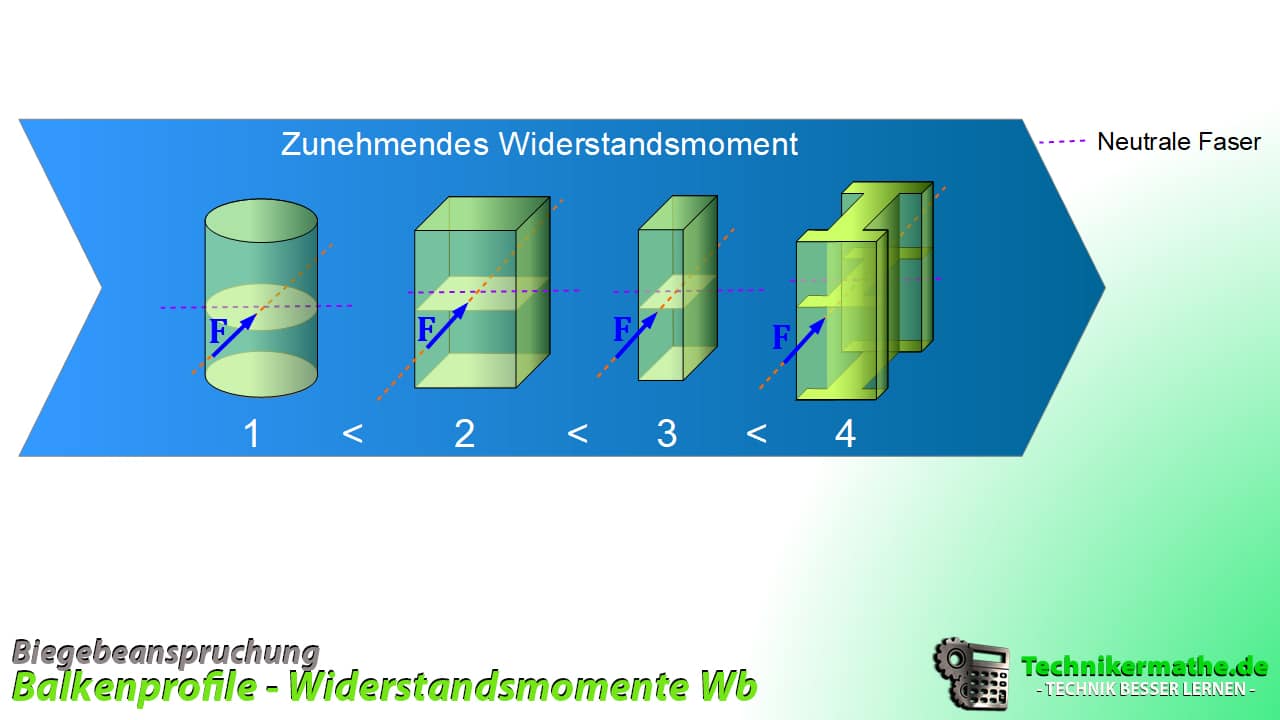
Biegebeanspruchung - Zunehmende Widerstandsmomente - Balkenprofile — Biegebeanspruchung – Zunehmende Widerstandsmomente – Balkenprofile

Aber warum ist das so?…

Je mehr Material ich von der neutralen Faser (lila Linie) entferne umso größer ist das Widerstandsmoment. Das Fällt besonders im Vergleich zwischen Kreisquerschnitt und Doppel-T-Träger-Querschnitt auf.

Einige gängige Balkenprofile und ihre entsprechenden Widerstandsmomente:

Rechteckiger Hohlprofilbalken:
- Widerstandsmoment bezüglich der horizontalen Achse ( $I_x$ ): $\frac{ (b \cdot h^3 - (b - 2t) \cdot (h - 2t)^3)}{6}$
- Widerstandsmoment bezüglich der vertikalen Achse ( $I_y$ ): $\frac{(h \cdot b^3 - (h - 2t) \cdot (b - 2t)^3)}{6}$
  
  Hierbei sind $b =$ Breite, $h =$ Höhe und $t =$ Wandstärke des Profils.
I-Träger:
- Widerstandsmoment bezüglich der horizontalen Achse ( $I_x$ ): $\frac{ (b \cdot h^3 - (b - t_f) \cdot (h - 2t_f)^3}{ / 12 + A_f \cdot (d - (h - t_f))^2}$
- Widerstandsmoment bezüglich der vertikalen Achse ( $I_y$ ): $\frac{ h \cdot b^3 - (h - 2t_f) \cdot (b - t_f)^3)}{12}$
  
  Hierbei sind $b =$ Gesamtbreite des Trägers, $h =$ Gesamthöhe, $t_f =$ Flanschdicke, $A_f$ = Flanschfläche und $d =$ Abstand zwischen den Flanschschwerpunkten.
T-Träger:
- Widerstandsmoment bezüglich der horizontalen Achse ( $I_x$ ): $\frac{ (b_f \cdot h_f^3 + b_w \cdot h_w^3)}{ 12 + A_w \cdot (h_f + h_w - d)^2 }$
- Widerstandsmoment bezüglich der vertikalen Achse ( $I_y$ ): $\frac{ (h_f \cdot b_f^3 + h_w \cdot (b_w - d)^3)}{12}$
  
  Hierbei sind $b_f =$ Flanschbreite, $h_f =$ Flanschhöhe, $b_w =$ Stegflanschbreite, $h_w =$ Stegflanschhöhe, $A_w =$ Stegflanschfläche und $d =$ Stegstärke.

Bitte beachte, dass dies allgemeine Formeln für die Widerstandsmomente sind und je nach spezifischem Profil und dessen Dimensionen leicht variieren können. Es ist immer empfehlenswert, die genauen Spezifikationen des Balkenprofils zu überprüfen oder spezifische technische Tabellen oder Normen zu konsultieren, um genaue Werte zu erhalten.

Allgemeine Gleichung für eine Biegebeanspruchung

Die allgemeine Gleichung für eine Biegebeanspruchung unter Angabe von Biegemoment und Widerstandsmoment.

Biegebeanspruchung (allgemein)

$\sigma_b = \frac{M_b}{W_b}$

Kennzahlen

$\sigma_b =$ Biegebeanspruchung
$M_b =$ Biegemoment
$W_b =$ Widerstandsmoment

Flächenträgheitsmoment bei reiner Biegung

Flächenträgheitsmoment – Erklärung

Das Flächenträgheitsmoment, symbolisiert durch das Zeichen “I”, gibt an, wie der Querschnitt eines Materials gegenüber Biegung widerstandsfähig ist. Es hängt von der Geometrie des Querschnitts ab und wird normalerweise in Bezug auf eine neutrale Faser berechnet.

Das Flächenträgheitsmoment kann für unterschiedliche Querschnittsformen berechnet werden, z.B. für

einen Rechteckquerschnitt,
einen Kreisquerschnitt oder
einen Hohlquerschnitt.

Merk’s dir!

Die genaue Berechnungsmethode hängt von der spezifischen Querschnittsform ab.

Das Flächenträgheitsmoment ist eine wichtige Größe, da es direkt mit den Spannungen im Material in Zusammenhang steht. Je größer das Flächenträgheitsmoment ist, desto widerstandsfähiger ist der Querschnitt gegenüber Biegespannungen und desto geringer sind die Verformungen. Ein größerer Querschnitt mit einem größeren Flächenträgheitsmoment kann also höhere Biegemomente aufnehmen, ohne dass es zu Versagen oder übermäßigen Verformungen kommt.

Flächenträgheitsmoment – Formel

Definieren wir nun noch das Flächenträgheitsmoment $I_y$ der 2. Ordnung in Bezug auf die y-Achse.

Flächenträgheitsmoment

$I_y = \int_A d^2 dA$

Kennzahlen

$I_y =$ Flächenträgheitsmoment
$d =$ Abstand zur neutralen Faser
$A =$ Querschnittsfläche

Muss ich das alles ausrechnen…

Nein, denn in den meisten Fällen lassen sich das Flächenträgheitsmoment und das Widerstandsmoment für unterschiedlichste geometrische Formen aus Tabellenwerken ablesen, wodurch eine eigenständige Berechnung nicht mehr notwendig ist.

Was kommt als Nächstes?

Nachdem wir uns mit der ersten Form der Spannungen bei Biegung befasst haben, gehen wir im kommenden Kurstext auf die Schubspannungen als Form der Beanspruchung ein.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++