In diesem Kurstext gehen wir auf die Beanspruchungsart Zug in der Maschinentechnik näher ein. Dabei behandeln wir das Hooke’sche Gesetz [Hookesche Gesetz] und den Elastizitätsmodul.
Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.
Hookesche Gesetz – Allgemein
Das Hooke’sche Gesetz ist ein physikalisches Gesetz, welches beschreibt, wie sich elastische Materialien wie Federn oder Gummi verhalten, wenn sie einer Kraft ausgesetzt werden. Es besagt, dass die Ausdehnung oder Stauchung eines solchen Materials direkt proportional zur auf sie ausgeübten Kraft ist.
Anders ausgedrückt: Je stärker die Kraft, desto mehr wird das Material ausgedehnt oder zusammengedrückt.
Das Hookesche Gesetz lässt sich mathematisch durch eine einfache Formel ausdrücken: F = kx. Dabei steht F für die auf das Material ausgeübte Kraft, x für die daraus resultierende Ausdehnung oder Stauchung und k für eine Konstante, die als Federkonstante bezeichnet wird.
Die Federkonstante gibt an, wie stark das Material ist und wie viel Kraft benötigt wird, um es auszudehnen oder zusammenzudrücken.
Das Hookesche Gesetz gilt nur für elastische Materialien, die nach Entfernung der Kraft in ihre ursprüngliche Form zurückkehren.
Das Gesetz findet Anwendung in vielen Bereichen, wie zum Beispiel in der Konstruktion von Brücken, Gebäuden oder in der Mechanik von Fahrzeugen.
Hookesche Gesetz für eine Zugbeanspruchung
Für die Relation zwischen Spannung ![]() und Dehnung
und Dehnung ![]() im linear-elastischen Bereich können wir das Hookesche Gesetz heranziehen.
im linear-elastischen Bereich können wir das Hookesche Gesetz heranziehen.
Formal sieht das wie folgt aus:
![]()
Kennzahlen:
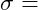 Spannung
Spannung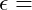 Dehnung
Dehnung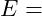 Elastizitätsmodul
Elastizitätsmodul
E-Modul für Zugkräfte
Der Elastizitätsmodul ![]() oder auch E-Modul ist der Proportionalitätsfaktor zwischen den beiden Größen und gibt die Steigung der Hookeschen Geraden wieder. Als wichtige Materialgröße, erlaubt er uns Aussagen zum elastischen Verhalten eines Materials zu treffen, unabhängig davon ob es sich um eine Druck- oder Zugbelastung handelt [identischer Wert].
oder auch E-Modul ist der Proportionalitätsfaktor zwischen den beiden Größen und gibt die Steigung der Hookeschen Geraden wieder. Als wichtige Materialgröße, erlaubt er uns Aussagen zum elastischen Verhalten eines Materials zu treffen, unabhängig davon ob es sich um eine Druck- oder Zugbelastung handelt [identischer Wert].
Angegeben wird der E-Modul mit der Einheit ![]()
Durch Umstellen des Hookeschen Gesetzes können wir den E-Modul auch direkt aus der Spannung und der Dehnung berechnen. Diese Werte erhalten wir wiederum aus dem Zugversuch.
![]()
Mit den Gleichungen für die Spannung und Dehnung (eingesetzt)

Kennzahlen:
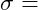 Spannung
Spannung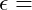 Dehnung
Dehnung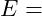 Elastizitätsmodul
Elastizitätsmodul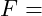 Kraft
Kraft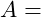 Querschnittsfläche
Querschnittsfläche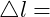 Längenänderung
Längenänderung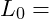 Ausgangslänge.
Ausgangslänge.
Ferner können wir das Hookesche Gesetz jeweils nach ![]() und
und ![]() auflösen:
auflösen:
![]()
Kennzahlen:
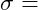 Spannung
Spannung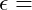 Dehnung
Dehnung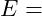 Elastizitätsmodul
Elastizitätsmodul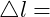 Längenänderung
Längenänderung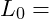 Ausgangslänge.
Ausgangslänge.
![]()
Kennzahlen:
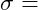 Spannung
Spannung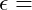 Dehnung
Dehnung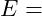 Elastizitätsmodul
Elastizitätsmodul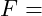 Kraft
Kraft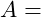 Querschnittsfläche
Querschnittsfläche
wobei das Produkt aus ![]() und
und ![]()
 Dehnsteifigkeit
Dehnsteifigkeit
ist.
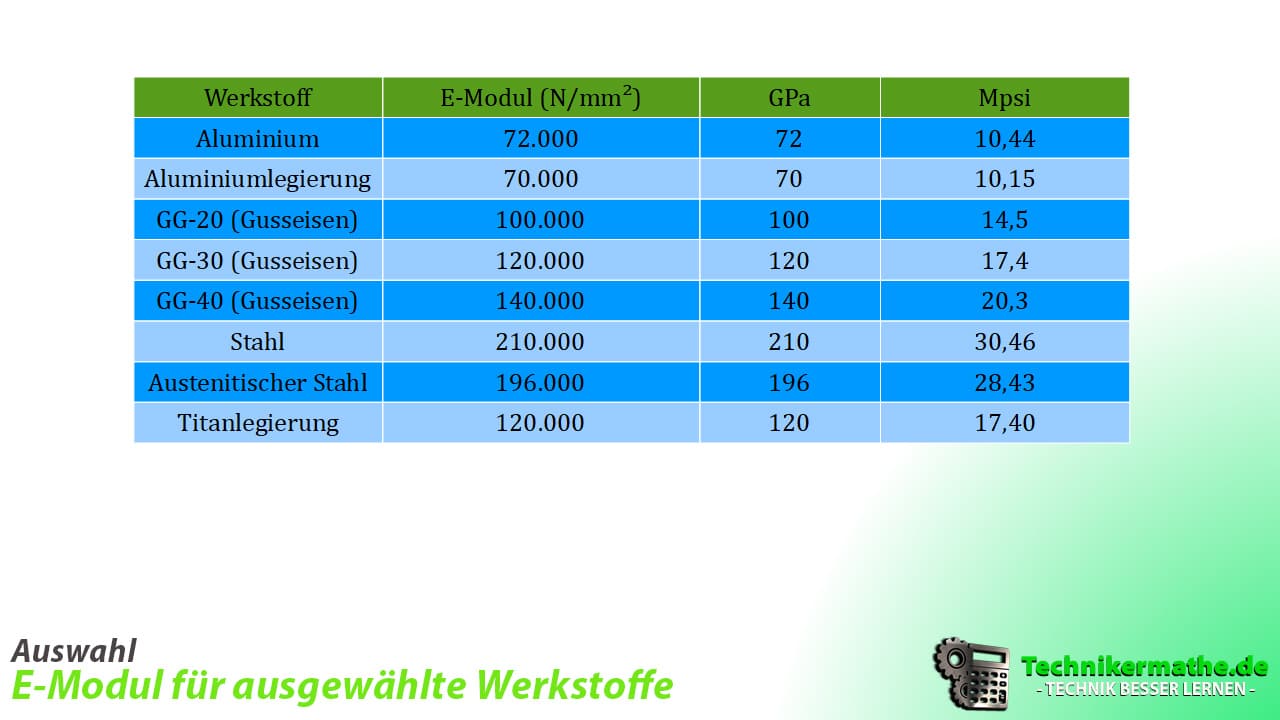
Welchen Wert der E-Modul annimmt hängt vom jeweiligen Werkstoff ab. In der nachfolgenden Abbildung siehst du einige typische Werte für den E-Modul.
Beispiel: Berechnung des E-Modul
Zum Abschluss betrachten wir nun ein kleines Rechenbeispiel, bei welchem unter anderem der E-Modul errechnet werden soll.
Im Labor wird ein Zugversuch durchgeführt und nun soll der E-Modul errechnet werden.
Der verwendete Rundstab hat einen Durchmesser von ![]()
Die Ausgangslänge des Rundstabes beträgt ![]()
Die Prüfkraft wird mit ![]() angegeben.
angegeben.
Es stellt sich eine Verlängerung von ![]() ein.
ein.
- Wie groß ist die Zugspannung
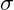 ?
? - Wie groß ist die elastische Dehnung
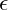 ?
? - Welchen Wert besitzt der E-Modul
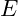 ?
?
Bestimmung der Zugspannung
![]()
Im ersten Schritt müssen wir noch die Querschnittsfläche ![]() des Rundstabes berechnen:
des Rundstabes berechnen:
![]()
![]()
![]()
![]()
![]()
Im zweiten Schritt müssen wir noch die Kraft in die passende Einheit umrechnen:
![]()
Im letzten Schritt können wir die Werte einsetzen und die Spannung berechnen:
![]()
![]()
![]()
Die Zugspannung beträgt 63,66 N/mm².
Bestimmung der Dehnung
![]()
![]()
![]()
Die Dehnung beträgt 2 %.
Bestimmung des Elastizitätsmodul
![]()
![]()
![]()
Der E-Modul beträgt 1591,55 N/mm².
Nachdem wir uns mit dem Thema Hookesche Gesetz und Elastizitätsmodul bei Zugkräften befasst haben, gehen wir im nächsten Abschnitt über zu den Druckbeanspruchungen sowie der Flächenpressung.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






