[ME1] Biegebeanspruchung – Klausuraufgabe

In diesem Kurstext stellen wir dir basierend auf dem vorangegangenen Kurstext eine typische Klausuraufgabe zur Biegebeanspruchung vor. Dabei bedienen wir uns des bereits behandelten Beispiels, nun jedoch mit Zahlenwerten.

Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.

Biegebeanspruchung Klausuraufgabe: Ausgangssituation

Beispiel!

Erneute betrachten wir das Wellenlager, welches auf einem Stahlträger [Balken] aufliegt. Dieser Balken liegt zudem auf einem Lagerbock. Der Lagerbock besteht aus einem Festlager A und einem Loslager B.

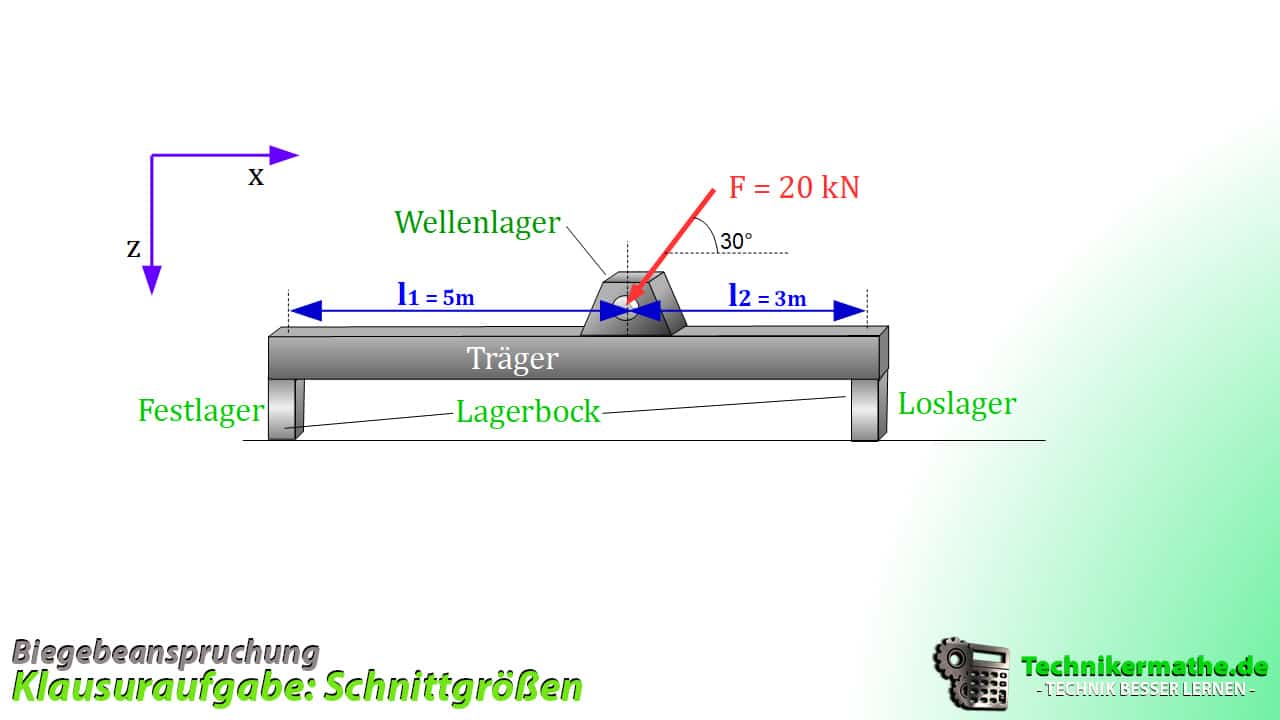
Klausuraufgabe: Biegebeanspruchung - Schnittgrößen berechnen — Klausuraufgabe: Biegebeanspruchung – Schnittgrößen berechnen

Das Wellenlager wird durch eine schräge Kraft F angegriffen.

Aufgabenstellung

Deine Aufgabe besteht darin, für diesen Balken alle Schnittgrößen zu ermitteln.

Gegeben:

$F = 20 kN$ : Schräg angreifende Kraft
$\alpha = 30°$ : Winkel der angreifenden Kraft [ = Angriffswinkel]
$l_1 = 5 m$ : Abstand Festlager zu Mitte Wellenlager [Angriffspunkt der Kraft F]
$l_2 = 3 m$ : Abstand Loslager zu Mitte Wellenlager [Angriffspunkt der Kraft F]
$a = 0,5 m$ : Abstand zwischen Balken und angreifender Kraft [ = Hebelarm]

Gesucht:

Lagerkräfte und anschließend Schnittgrößen!

Wir gehen wie bereits behandelt nach dem bekannten Muster vor:

Freischneiden [Mechanisches Ersatzbild]
Lagerkräfte einzeichnen [Mechanisches Ersatzbild]
Lagerkräfte ermitteln [Gleichgewichtsbedingungen]
Schnittgrößen ermitteln

Merk’s dir!

Wichtige Annahmen zur weiteren Bearbeitung der Aufgabe:

Beanspruchungen: Dem äußeren Moment stehen innere Spannungen gegenüber, welche

nach Bernoulli: Querschnitte bleiben eben! [Für linearen Verformungszustand erforderlich]
nach St. Vernant: Ausreichender Abstand zwischen Einspannung und Angriffsstelle [Verhältnis | Dimensionierung des Balkens ( Länge zu Höhe: 5 : 1) $l \le 5 \cdot h$ ]

über die Querschnittsfläche des Balkens als linear verteilt angenommen werden.

Lösung 1: Freischneiden

Klausuraufgabe: Schnittgrößen bei Biegung [Freischnitt]

Der Freischnitt beinhaltet sowohl die Kraft $F$ als auch die Lagerkräfte $A_x, A_z, B_z$ . Die Kraftkomponenten $F_x$ und $F_z$ müssen noch angepasst werden, da es sich um eine schräge Kraft handelt, bei welcher der Winkel $\alpha$ gegeben ist.

Lösung 2: Lagerkräfte einzeichnen, Kraftkomponenten eintragen

Im ersten Schritt zerlegen wir die schräge Kraft $F$ in ihre Kraftkomponenten $F_x$ und $F_z$ und visualisieren dies erneut in unserem Freischnitt:

Klausuraufgabe: Einzeichnen der Lagerkräfte und Kraftkomponenten

Lösung 3: Lagerkräfte ermitteln

Wir bestimmen die drei Lagerkräfte am ungeschnittenen Balken. Hierzu stellen wir die drei Gleichgewichtsbedingungen in der Ebene auf.

Horizontale Gleichgewichtsbedingung
Vertikale Gleichgewichtsbedingung
Momentengleichgewichtsbedingung

Horizontale GGB:

$\rightarrow : A_x = F \cdot cos(30) = 0$

Umstellen ergibt:

$A_x = F \cdot cos(30)$

Einsetzen ergibt:

$A_x = 30 kN \cdot cos(30) = 17,32 kN$

Vertikale GGB:

$\uparrow : A_z + B_z - F \cdot sin(30) = 0$

Umstellen ergibt:

$A_z + B_z = F \cdot sin(30)$

Einsetzen ergibt:

$A_z + B_z = 30 kN \cdot cos(30) = 10 kN$

Momentengleichgewichtsbedingung

Um nun die beiden noch unbekannten Lagerkräfte bestimmen zu können, nutzen wir jetzt die Momentengleichgewichtsbedingung,

Merk’s dir!

Die Position, an welcher die Gleichgewichtsbedingung folglich am logischsten angewendet wird, ist dort wo die meisten unbekannten Kraft aus der Betrachtung herausfallen.

In unserem Fall ist dies an den Stellen der beiden Lager A und B gegeben. Wählen wir nun das Lager A als unseren Bezugspunkt aus, so fallen die beiden Lagerkräfte aus der Gleichung heraus, zumal deren Wirkungslinie den Bezugspunkt schneiden, wo durch kein Hebelarm wirkt.

Die Lagerkraft $B_z$ können wir somit berechnen.

Der Drehsinn…

Immer wenn du vor einer Aufgabe sitzt, bei welcher das Momentengleichgewicht bestimmt werden soll, musst du den Drehsinn berücksichtigen. Handelt es sich um eine Linksdrehung so geht der Term positiv in den Berechnung ein. Liegt hingegen eine Rechtsdrehung vor, so geht der Term negativ in die Berechnung ein.

Lösung 3: Lagerkräfte ermitteln – Fortsetzung

Momentengleichgewicht am Lager A:

$\curvearrowleft A: B_z (l_1 + l_2) + F \cdot cos(30) \cdot a - F \cdot sin(30) \cdot l_1 = 0$

Auflösen der Gleichung nach $B_z$ ergibt:

$B_z = \frac{- F \cdot cos(30) \cdot a + F \cdot sin(30) \cdot l_1}{(l_1 + l_2)}$

Einsetzen der bekannten Größen:

$B_z = \frac{- 30 kN \cdot cos(30) \cdot 0,5 + 30 kN \cdot sin(30) \cdot 5}{(5 + 3)}$

Als Ergebnis erhalten wir dann:

$B_z = 5,17 kN$

Nachdem wir nun $B_z$ errechnet haben, können wir mit Hilfe der vertikalen Gleichgewichtsbedingung (vertikale GGB) noch die verbliebene unbekannte Größe $A_z$ berechnen.

$A_z + B_z = 10 kN$

Auflösen nach $A_z$ :

$A_z = 10 kN - B_z$

Einsetzen des Wertes für $B_Z$

$A_z = 10 kN - 5,17 kN$

$A_z = 4,83 kN$

Merk’s dir!

Der gesamte Balken befindet sich im Gleichgewicht, da

$A_z + B_z = F_z$

und

$A_x = F_x$

gilt.

Merk’s dir!

Es empfiehlt sich die Schnitte immer an den Stellen zu setzen, dort wo eine Belastungsänderung eintritt.

Die umfasst Änderungen von

Kräften
Momenten

unter anderem durch

Gelenke
Belastungssprünge

Lösung 4: Schnittgrößen

Klausuraufgabe: Einzeichnen der Lagerkräfte und Kraftkomponenten

Nach einem Schnitt lässt sich entweder mit dem linken oder dem rechten Schnittufer rechnen. Die Wahl sollte immer auf die Seite fällen, wo weniger unbekannte Größen zu berechnen sind.

Daher fällt bei einem Schnitt von Stelle 4 unsere Wahl auf das rechte Schnittufer, da hier lediglich $F_x$ und $F_z$ berücksichtigt werden müssen.

Bei linken Schnittufer sind es mit $A_x , A_z$ und $B_z$ hingegen 3 Kräfte. Das Ergebnis ist aber letztlich identisch.

Linkes Schnittufer

Dennoch betrachten wir jetzt die Schnittgrößen am linken Schnittufer:

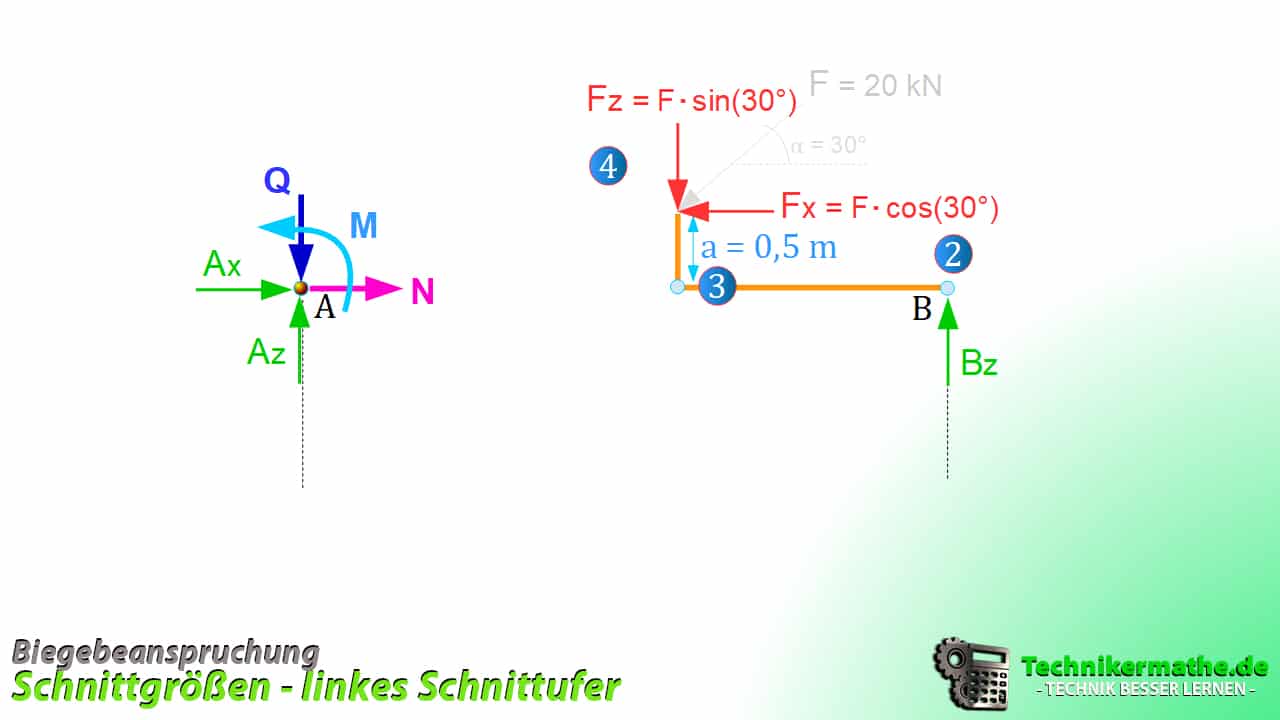
Stellen wir nun die Gleichgewichtsbedingungen hierzu auf:

$\uparrow : - Q + A_z = 0 \rightarrow Q = A_z = 4,83 kN$

$\rightarrow: N + A_x = 0 \rightarrow N = A_x = -17,32 kN$

$\curvearrowleft: M = 0$

Rechtes Schnittufer

$\uparrow : Q + B_z = 0 \rightarrow Q = B_z = - 5,17 kN$

$\rightarrow: - N = 0 \rightarrow N = 0$

$\curvearrowleft: - M = 0 \rightarrow M = 0$

Schnitt links am vertikalen Balken

Nun führen wir einen weiteren Schnitt links neben dem senkrechten Balken durch und stellen die Gleichgewichtsbedingung auf.

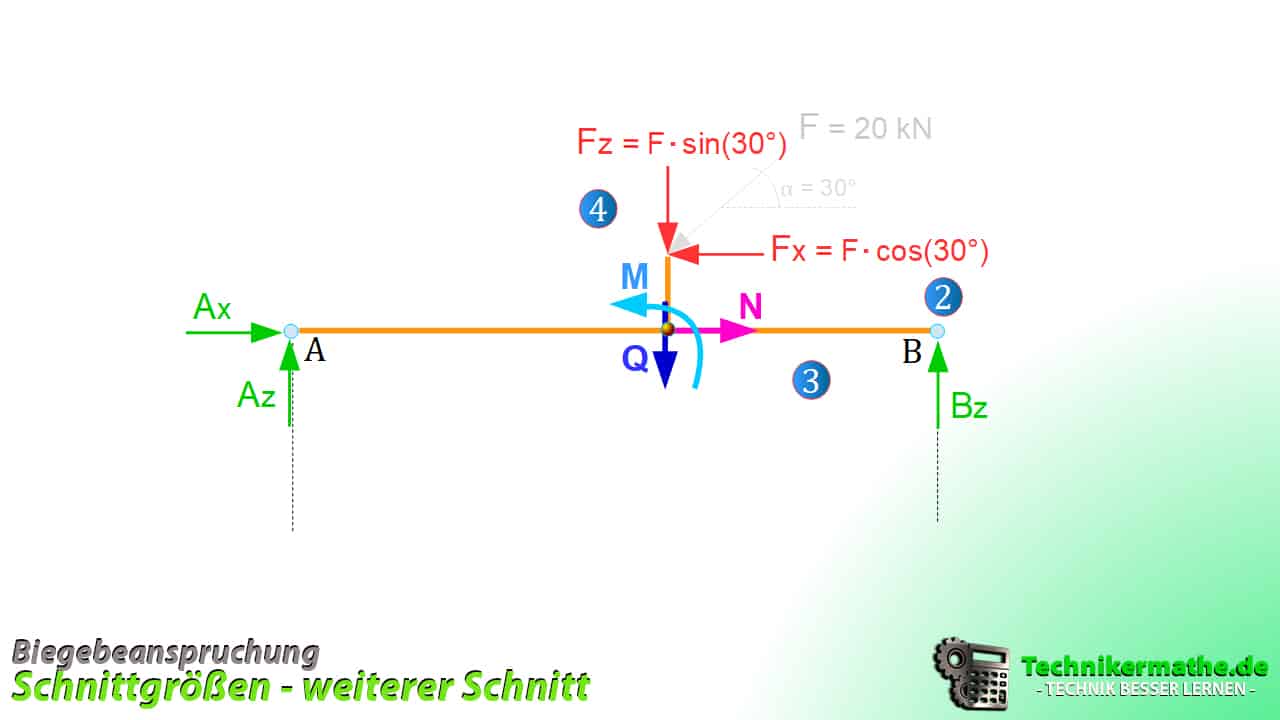
Schnittgrößen - weiterer Schnitt

$\uparrow : - Q + A_z = 0 \rightarrow Q = A_z = 4,83 kN$

$\rightarrow: N + A_x = 0 \rightarrow N = - A_x = - 17,32 kN$

$\curvearrowleft: M - A_z \cdot l_1 = 0 \rightarrow M = 4,83 kN \cdot 5 m = 24,15 kNm$

Schnitt rechts am vertikalen Balken

Nun führen wir einen weiteren Schnitt rechts neben dem senkrechten Balken durch und stellen die Gleichgewichtsbedingung auf.

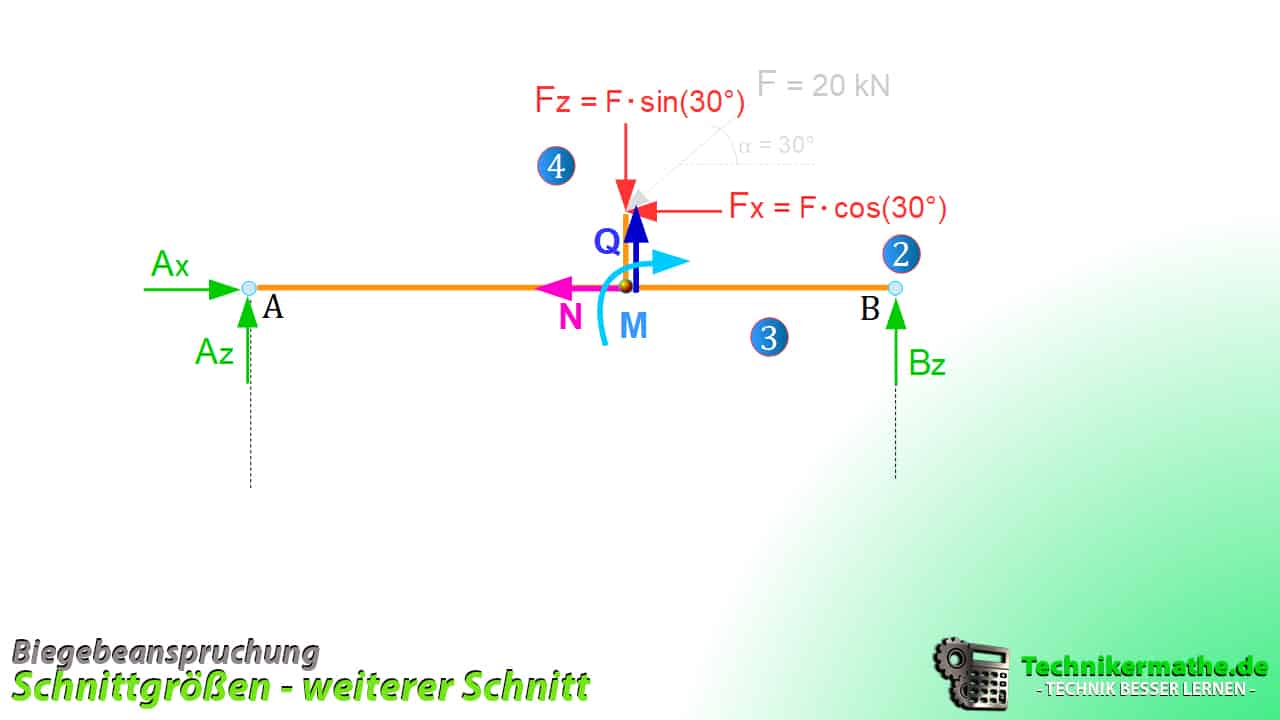
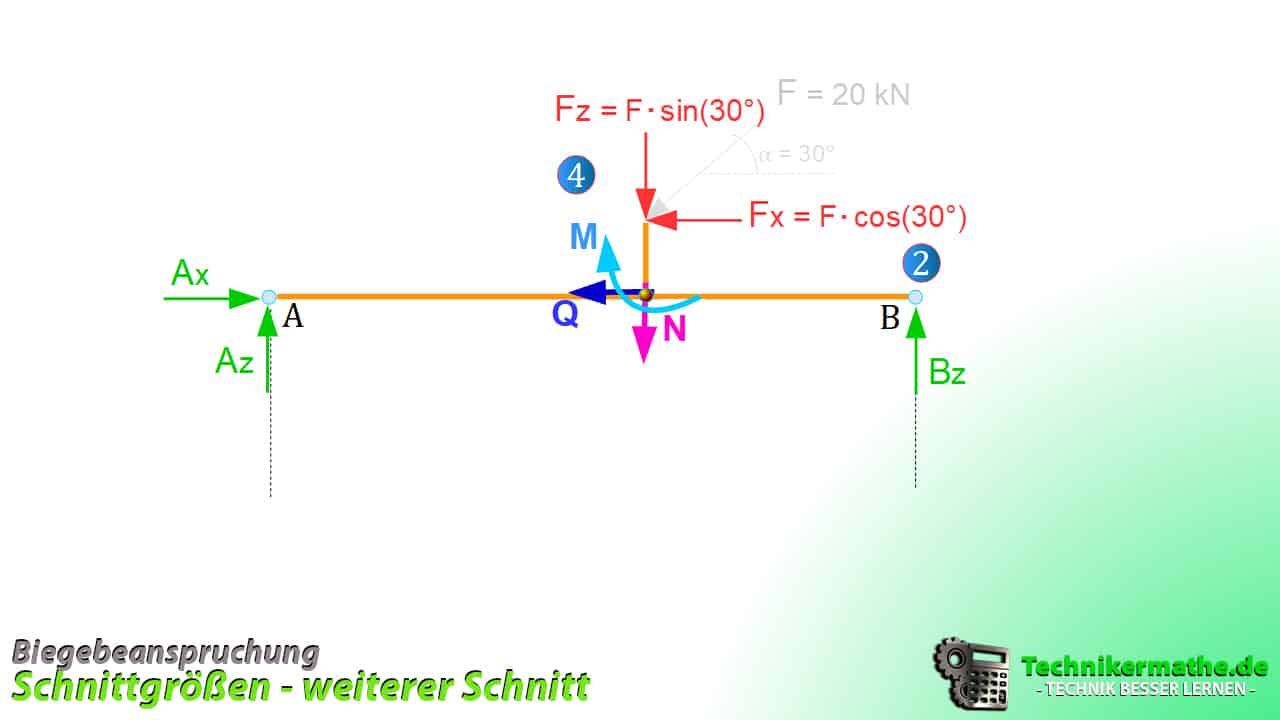
Schnittgrößen - weiterer Schnitt

$\uparrow : Q + B_z = 0 \rightarrow Q = - B_z = - 5,17 kN$

$\rightarrow: - N = 0 \rightarrow N = 0$

$\curvearrowleft: - M + B_z \cdot l_2 = 0 \rightarrow M = 5,17 kN \cdot 3 m = 15,51 kNm$

Jetzt sind alle Kräfte im unteren Balken (horizontal) ermittelt worden. Nun betrachten wir die Kräfte oberhalb vom Balken (vertikal) nachdem wir diesen gedanklich vom unteren Balken getrennt haben.

Schnittgrößen - weiterer Schnitt

$\uparrow : Q + F_x = 0 \rightarrow Q = - F_x = - 17,32 kN$

$\rightarrow: - N - F_z = 0 \rightarrow N = - F_z = - 10 kN$

$\curvearrowleft: - M + F_x \cdot a = 0 \rightarrow M = 17,32 kN \cdot 0,5 m = 8,66 kNm$

Gedanklich verlagern wir den Schnitt nun nach oben an die Position 4:

$\uparrow : Q + F_x = 0 \rightarrow Q = - F_x = - 17,32 kN$

$\rightarrow: - N - F_z = 0 \rightarrow N = - F_z = - 10 kN$

$\curvearrowleft: - M 0 \rightarrow M = 0$

Mit der Bestimmung der Schnittgrößen schließen wir dieses Beispiel ab.

Was kommt als Nächstes?

Nachdem wir uns mit dem Zahlenbeispiel für die Biegebeanspruchung befasst haben, gehen wir im kommenden Kurstext auf die Torsion als Form der Beanspruchung ein.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++