In diesen Kursabschnitt befassen wir uns ausführlich mit dem Thema Beanspruchungsfälle & Werkstoffkennwerte. Dabei gehen wir auf Statische Beanspruchungen, Dynamische Beanspruchungen, sowie Versagensgrenzen und Verformungen im Detail ein.
Für ein optimales Verständnis helfen dir einige anschauliche Beispiele und abschließende, umfangreiche Abbildungen zu dem Thema, sowie ein zusammenfassender Videoclip.
Beanspruchungsfälle – Grundlagen
Beanspruchungsfälle in der Maschinentechnik beziehen sich auf die verschiedenen Situationen oder Szenarien, in denen Maschinen und Bauteile verschiedenen Arten von Belastungen und Beanspruchungen ausgesetzt sind.

Das Verständnis dieser Beanspruchungsfälle ist entscheidend, um die richtigen Materialien und Konstruktionsmethoden auszuwählen, die die gewünschte Leistung und Haltbarkeit gewährleisten.
Hier sind einige grundlegende Beanspruchungsfälle
-
Statische Beanspruchung:
- Bei statischer Beanspruchung bleiben die auf das Bauteil wirkenden Kräfte konstant. Das bedeutet, dass die Kräfte und Momente nicht mit der Zeit variieren. Beispiele sind das Gewicht eines statischen Bauteils oder eine ruhende Struktur.
-
Dynamische Beanspruchung:
- Bei dynamischer Beanspruchung variieren die Kräfte und Momente mit der Zeit. Dies kann periodisch, zufällig oder schlagartig sein. Beispiele sind die Bewegung eines Fahrzeugs oder die Vibration eines Motors.
-
Stoßbelastung:
- Stoßbelastungen treten auf, wenn ein plötzlicher, impulsartiger Kraftaufprall auf ein Bauteil erfolgt. Dies kann beispielsweise bei Maschinen auftreten, die mit schweren Lasten arbeiten.
-
Torsion:
- Torsionale Beanspruchung tritt auf, wenn ein Bauteil gedreht wird. Ein typisches Beispiel ist die Torsion einer Welle in einem Getriebe oder einem Antriebssystem.
-
Thermische Beanspruchung:
- Thermische Beanspruchung resultiert aus Temperaturschwankungen, die dazu führen können, dass Materialien sich ausdehnen und zusammenziehen. Dies kann in Motoren, Ofenrohren und anderen hitzeexponierten Anwendungen auftreten.
-
Korrosion:
- Korrosion ist eine chemische Beanspruchung, bei der Materialien durch Umwelteinflüsse, wie Feuchtigkeit oder aggressive Chemikalien, geschädigt werden. Dies kann in Konstruktionen und Anlagen auftreten, die im Freien oder in feuchten Umgebungen arbeiten.
-
Ermüdungsbelastung:
- Ermüdungsbelastung resultiert aus wiederholten Lastwechseln oder Schwingungen, die die Materialermüdung und letztendlich das Versagen eines Bauteils verursachen können. Dies tritt beispielsweise bei Rüttelmaschinen auf.
-
Schubbelastung:
- Schubbelastung tritt auf, wenn benachbarte Schichten eines Materials in unterschiedliche Richtungen verschoben werden, was zu Scherspannungen führt. Dies kann in Bolzen und Verbindungselementen auftreten.
Die Identifizierung und Bewertung dieser Beanspruchungsfälle ist von entscheidender Bedeutung, um sicherzustellen, dass Maschinen und Bauteile den erforderlichen Leistungs- und Sicherheitsanforderungen gerecht werden. Ingenieure und Techniker müssen diese Faktoren bei der Auswahl von Materialien und der Konstruktion von Bauteilen berücksichtigen, um Ausfälle zu minimieren und die Lebensdauer von Maschinen zu maximieren.
Werkstoffkennwerte – Grundlagen
Werkstoffkennwerte sind wichtige Parameter/ Größen in der Maschinentechnik, um die Auswahl von geeigneten Materialien für Maschinenkomponenten und die Analyse von Beanspruchungen zu erleichtern.
Hier sind einige grundlegende Werkstoffkennwerte und deren Bedeutung in der Maschinentechnik:
-
Zugfestigkeit (Rm):
- Die Zugfestigkeit ist die maximale Zugspannung, die ein Material unter axialer Belastung aushält, bevor es versagt. Sie ist ein wichtiger Faktor bei der Auswahl von Materialien für Bauteile, die Zugkräften ausgesetzt sind.
-
Streckgrenze (Re):
- Die Streckgrenze ist die Spannung, bei der ein Material eine dauerhafte Dehnung zeigt, ohne plastische Verformung. Sie ist ein Maß für die Elastizität eines Materials und zeigt den Punkt an, an dem es in den plastischen Bereich übergeht.
-
Bruchdehnung (A):
- Die Bruchdehnung ist ein Maß für die Dehnbarkeit eines Materials und gibt an, wie viel es sich unter Zugspannung verformen kann, bevor es versagt. Ein hoher Wert zeigt eine hohe Duktilität an.
-
Elastizitätsmodul (E):
- Der Elastizitätsmodul, auch bekannt als E-Modul oder Young’s Modulus, gibt an, wie steif ein Material ist. Es beschreibt die Beziehung zwischen Spannung und Dehnung im elastischen Bereich des Materials.
-
Härte:
- Die Härte eines Materials gibt an, wie widerstandsfähig es gegenüber plastischer Verformung oder Eindringen ist. Verschiedene Härteprüfverfahren, wie Brinell, Vickers oder Rockwell, werden angewendet.
-
Schlagzähigkeit:
- Die Schlagzähigkeit ist die Fähigkeit eines Materials, plötzlichen Schlagbelastungen standzuhalten, ohne zu versagen. Dies ist besonders wichtig bei Bauteilen, die Schlagbelastungen ausgesetzt sind, wie Zahnräder oder Schlagwerkzeuge.
-
Wärmeleitfähigkeit (λ):
- Die Wärmeleitfähigkeit gibt an, wie gut ein Material Wärme leitet. Dies ist wichtig, wenn es darum geht, die Temperaturverteilung in einem Bauteil zu verstehen und zu steuern.
-
Temperaturbeständigkeit:
- Die Temperaturbeständigkeit eines Materials bezieht sich auf seine Fähigkeit, bei hohen oder niedrigen Temperaturen stabil zu bleiben, ohne dass es zu einem Versagen oder einer Veränderung seiner mechanischen Eigenschaften kommt.
-
Dichte (ρ):
- Die Dichte eines Materials gibt an, wie viel Masse es pro Volumeneinheit hat. Dies ist wichtig bei der Dimensionierung von Bauteilen und bei der Berechnung von Belastungen.
-
Korrosionsbeständigkeit:
- Korrosionsbeständigkeit ist entscheidend, wenn Materialien in Umgebungen eingesetzt werden, in denen sie aggressiven chemischen Substanzen oder Feuchtigkeit ausgesetzt sind.
Die Kenntnis dieser Werkstoffkennwerte ist für Ingenieure und Techniker von großer Bedeutung, um sicherzustellen, dass die ausgewählten Materialien den Anforderungen der jeweiligen Anwendung entsprechen und die gewünschten mechanischen Eigenschaften aufweisen. Je nach den spezifischen Anforderungen der Maschinentechnik können unterschiedliche Werkstoffe mit den passenden Kennwerten erforderlich sein.
Statische Beanspruchung – Grundlagen
Eine statische Beanspruchung in der Maschinentechnik bezieht sich auf eine Form der mechanischen Beanspruchung, bei der die auf ein Bauteil oder eine Struktur wirkenden Kräfte und Momente konstant sind und nicht mit der Zeit variieren.
Dies bedeutet, dass die angewandten Belastungen und Momente über einen längeren Zeitraum stabil und unverändert bleiben. Auch die Wirkrichtung der Kraft oder Momente ist gleichbleibend.
Wichtige Werkstoffkennwerte für eine statische Beanspruchung sind die Streckgrenze und die Zugfestigkeit. Letzterer Wert kann am einfachsten mit dem Zugversuch ermittelt werden.
Beispiel für eine statische Beanspruchung

Legt man Objekte [Stifte & Schwamm] mit einem ausreichenden Gewicht auf eine gelagerte Fläche [Ablage] so entsteht eine statische Beanspruchung. Letztere entsteht durch die konstant nach unten wirkenden Kräfte ![]() [rote Pfeile]. Es handelt sich um die Gewichtskraft, welche bedingt durch die Erdanziehung vertikal nach unten wirkt (Wirkrichtung).
[rote Pfeile]. Es handelt sich um die Gewichtskraft, welche bedingt durch die Erdanziehung vertikal nach unten wirkt (Wirkrichtung).
Darstellung einer statischen Beanspruchung im Diagramm
Eine statische Beanspruchung kennzeichnet sich dadurch, dass eine Last aufgebracht wird und dann auf einem konstanten Wert gehalten wird.
Wie sich dies grafisch darstellen lässt, siehst du in der nachfolgenden Abbildung.
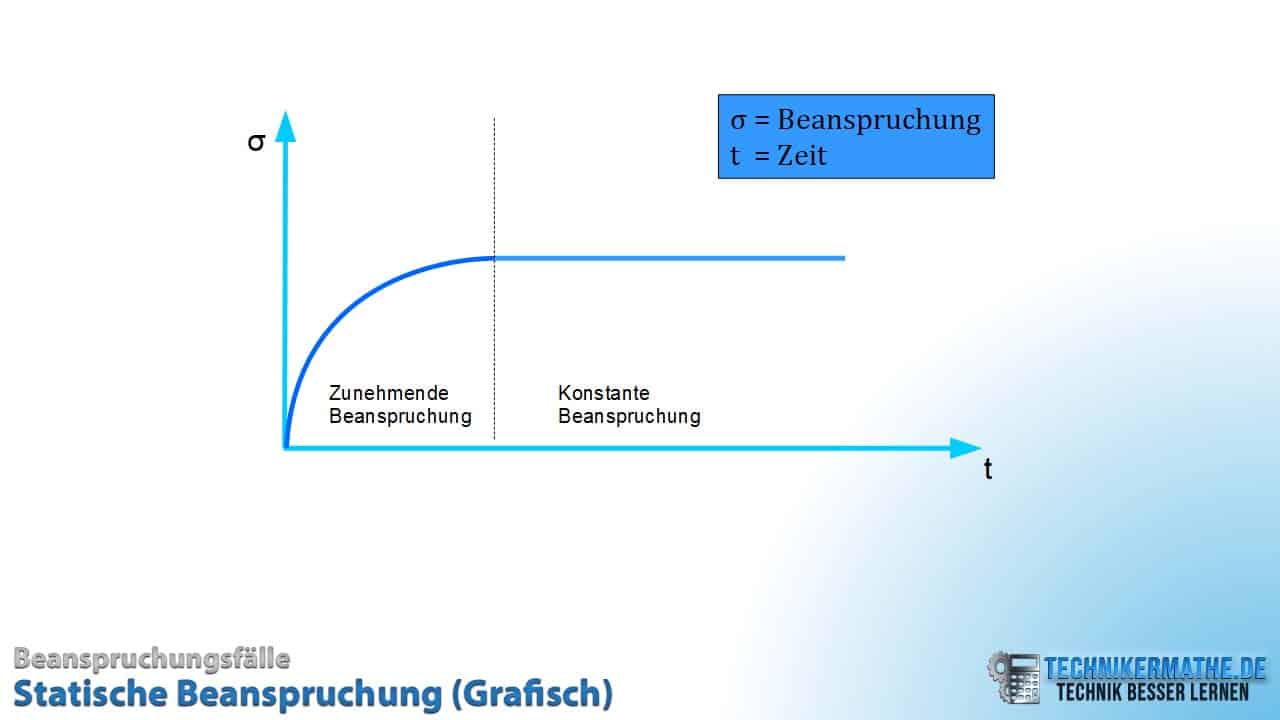
Im Diagramm werden die Spannung ![]() (y-Achse) und die Zeit
(y-Achse) und die Zeit ![]() (x-Achse) abgetragen.
(x-Achse) abgetragen.
- Dunkelblauer Kurvenbereich: Zu Beginn startet die Kurve im Nullpunkt (
 , und
, und  ). Anschließend steigt die Kurve zuerst proportional an und fällt anschließend ab.
). Anschließend steigt die Kurve zuerst proportional an und fällt anschließend ab. - Hellblauer Kurvenbereich: Danach verläuft die Kurve horizontal. Das bedeutet, dass sich die Spannung ab diesen Zeitpunkt nicht mehr verändert.
Versagensgrenzen – Grundlagen
Die Versagensgrenzen in der Maschinentechnik beziehen sich auf die kritischen Grenzwerte von mechanischen Beanspruchungen und Belastungen, bei denen ein Bauteil, eine Maschine oder eine Struktur das Risiko des Versagens erreicht.
Diese Grenzen sind wichtig, um die Sicherheit und Zuverlässigkeit von Maschinen und Bauteilen zu gewährleisten.
Es gibt verschiedene Arten von Versagensgrenzen, die in der Maschinentechnik berücksichtigt werden, darunter:
-
Streckgrenze (Re): Dies ist die Spannung, bei der ein Material eine dauerhafte Dehnung zeigt, ohne plastische Verformung. Sie ist eine wichtige Versagensgrenze, da sie anzeigt, ab welcher Belastung ein Material nicht mehr in seinen ursprünglichen Zustand zurückkehrt.
-
Zugfestigkeit (Rm): Die Zugfestigkeit ist die maximale Spannung, die ein Material unter axialer Belastung aushalten kann, bevor es bricht. Dies ist ein wichtiger Wert, um die Tragfähigkeit eines Materials zu bewerten.
-
Ermüdungsfestigkeit: Die Ermüdungsfestigkeit oder Ermüdungsgrenze ist die maximale Spannung, die ein Material für eine bestimmte Anzahl von Lastwechseln aushalten kann, bevor es Ermüdungsversagen aufweist. Sie ist entscheidend bei Anwendungen, die zyklischen Belastungen unterliegen, wie z.B. rotierende Wellen oder Federn.
-
Schlagzähigkeit: Die Schlagzähigkeit ist die Fähigkeit eines Materials, Stoßbelastungen ohne Versagen zu widerstehen. Materialien, die stoßbelastet werden, müssen über eine ausreichende Schlagzähigkeit verfügen.
-
Kriechfestigkeit: Die Kriechfestigkeit ist die Fähigkeit eines Materials, bei anhaltenden hohen Temperaturen und konstanter Belastung keine dauerhafte Verformung zu zeigen. Dies ist wichtig in Anwendungen, in denen Materialien hohen Temperaturen ausgesetzt sind.
-
Korrosionsbeständigkeit: Materialien müssen in korrosiven Umgebungen widerstandsfähig gegenüber chemischer Zersetzung und Rostbildung sein. Die Korrosionsbeständigkeit ist eine wichtige Versagensgrenze in solchen Umgebungen.
-
Temperaturbeständigkeit: Die Temperaturbeständigkeit bezieht sich auf die Fähigkeit eines Materials, bei extremen Temperaturen seine mechanischen Eigenschaften zu bewahren. In Anwendungen, bei denen Materialien extremen Temperaturen ausgesetzt sind, ist dies entscheidend.
-
Elastizitätsgrenze (Rp0.2): Die Elastizitätsgrenze ist die Spannung, bei der ein Material eine bleibende Dehnung von 0,2 % zeigt. Dies wird oft bei Werkstoffprüfungen verwendet, um die Dehnbarkeit und Elastizität eines Materials zu bewerten.
Die Kenntnis dieser Versagensgrenzen ist von entscheidender Bedeutung, um sicherzustellen, dass Materialien und Konstruktionen den Anforderungen und Belastungen in verschiedenen Maschinentechnikanwendungen standhalten. Man vergleicht also die Vergleichsspannungen mit den Werkstoffkennwerten des Zugversuchs.

Bei der Konstruktion von Maschinen und Strukturen müssen Ingenieure sicherstellen, dass die Beanspruchungen und Belastungen unterhalb dieser Versagensgrenzen liegen, um die Sicherheit und Zuverlässigkeit zu gewährleisten.
Diese Versagensgrenzen untersuchen die Vorgänge bei denen es zum Anriss und Bruch des Bauteils kommt, sowie die unzulässige plastische Verformung.
Anriss und Bruch
Sobald die vorliegende Belastung (Spannung) den Wert der Zugfestigkeit (Rm) überschreitet, steigt die Wahrscheinlichkeit eines Anrisses und eines darauf folgenden Bruchs exponentiell. Man spricht dann von der Grenzspannung ![]() .
.
Unzulässige plastische Verformung
Die unzulässige plastische Verformung tritt ein, sobald die Grenzspannung ![]() den Wert der oberen Streckgrenze
den Wert der oberen Streckgrenze ![]() , bzw. den Wert der Dehngrenze
, bzw. den Wert der Dehngrenze ![]() erreicht. In der Literatur findet sich für die Dehngrenze ebenfalls der alternative Begriff Proportionalitätsgrenze wieder.
erreicht. In der Literatur findet sich für die Dehngrenze ebenfalls der alternative Begriff Proportionalitätsgrenze wieder.
Werkstoffabhängigkeit
Die Grenzwerte sind werkstoffabhängig und müssen für jeden Werkstoff einzeln bestimmt werden. Darin liegt der Vorteil, dass je nach Art der Belastung der richtige Werkstoff ausgewählt werden kann. Anhand der Dehngrenze für verschiedene Werkstoffe soll diese verdeutlicht werden Die Dehngrenze wird üblicherweise in Pascal (Pa) gemessen. Ein Pascal entspricht einem Newton pro Quadratmeter (N/m²).
Hier sind einige Beispiele für Materialien und ihre Dehngrenzen in N/m² (Die Kennzahlen werden bei einer Raumtemperatur von 20°C ermittelt):
-
Stahl: Die Dehngrenze von Baustählen liegt typischerweise im Bereich von 250 bis 350 Megapascal (MPa), was 250.000 bis 350.000 N/m² entspricht.
-
Aluminium: Die Dehngrenze von unlegierten Aluminiumlegierungen liegt in der Regel zwischen 40 und 200 MPa, also 40.000 bis 200.000 N/m². Hochfeste Aluminiumlegierungen können Dehngrenzen von über 300 MPa haben.
-
Kupfer: Reines Kupfer hat eine Dehngrenze von etwa 100 MPa, was 100.000 N/m² entspricht.
-
Titan: Titanlegierungen haben Dehngrenzen im Bereich von 300 bis 1000 MPa, also 300.000 bis 1.000.000 N/m², abhängig von der Legierung und Wärmebehandlung.
-
Gusseisen: Die Dehngrenzen von Gusseisen variieren je nach Typ. Grauguss hat Dehngrenzen von etwa 170 bis 350 MPa (170.000 bis 350.000 N/m²), während Sphäroguss Dehngrenzen von etwa 350 bis 550 MPa (350.000 bis 550.000 N/m²) aufweisen kann.
-
Kunststoffe: Die Dehngrenzen von Kunststoffen variieren erheblich. Thermoplastische Kunststoffe wie Polyethylen haben niedrige Dehngrenzen, typischerweise im Bereich von 10 bis 30 MPa (10.000 bis 30.000 N/m²), während technische Thermoplaste wie Polycarbonat höhere Dehngrenzen von etwa 60 bis 80 MPa (60.000 bis 80.000 N/m²) aufweisen können.
Diese Beispiele sollen verdeutlichen, wie die Dehngrenzen in der Einheit Pascal (N/m²) für verschiedene Materialien aussehen können. Beachte, dass die genauen Werte je nach Legierung, Herstellungsprozess und Temperatur variieren können.
Instabilitätsfälle
Die Begriffe “knicken”, “kippen” und “beulen” beziehen sich auf unterschiedliche Formen von Instabilitäten oder Versagensmechanismen in mechanischen Strukturen.
Nachfolgend eine Definition der einzelnen Begriffe:
-
Knicken (Buckling):
- Das Knicken ist ein Instabilitätsfall, der in langen, schlanken Strukturen wie Säulen, Stäben oder Säulen auftritt. Wenn ein solches Bauteil unter axialer Druckbelastung steht, kann es instabil werden und seitlich ausknicken oder buckeln. Dies tritt aufgrund der Biegeinstabilität auf, bei der sich die Struktur plötzlich seitlich verschiebt und ihre Tragfähigkeit verliert. Die kritische Belastung, bei der das Knicken auftritt, hängt von der Geometrie und den Materialeigenschaften des Bauteils ab.
-
Kippen (Tipping):
- Das Kippen ist ein Instabilitätsfall, der auftritt, wenn ein Gegenstand oder eine Struktur aufgrund eines instabilen Gleichgewichts umkippt. Dies kann in verschiedenen Kontexten vorkommen, z. B. bei Baukranen, Möbeln oder Baumaschinen. Kippen tritt auf, wenn das Zentrum der Masse außerhalb des Stützpunktes oder der Stützfläche liegt und die resultierenden Kräfte das Gleichgewicht stören, wodurch die Struktur oder das Objekt umkippt.
-
Beulen (Buckling):
- Die Beule (oder Beulenbildung) ist ein weiterer Instabilitätsfall, der bei dünnen, flächigen Strukturen auftritt, wie beispielsweise bei Blechen, Platten oder Hülsen. Beulenbildung kann auftreten, wenn eine flächige Struktur einer axialen Druckbelastung ausgesetzt ist. An bestimmten Stellen kann die Oberfläche der Struktur nach innen oder außen ausweichen und eine Beule bilden. Dies geschieht normalerweise in Verbindung mit dem Knicken und wird oft als Beulenknicken bezeichnet. Die kritische Belastung, bei der Beulen auftritt, hängt von der Geometrie und den Materialeigenschaften des Bauteils ab.
In der Maschinentechnik und im Bauwesen ist es von entscheidender Bedeutung, diese Instabilitätsfälle zu verstehen und bei der Konstruktion von Strukturen und Bauteilen zu berücksichtigen, um Unfälle und Schäden zu vermeiden.
Dynamische Beanspruchung
Bei einer dynamischen Beanspruchung treten am Bauteil Lastwechsel auf. Diese Lastwechsel führen dann dazu, dass die zulässige Spannung in dem Bauteil sinkt. Dynamische Beanspruchungen werden unter dem Begriff Schwingungen erfasst.
Ein Bruch kann selbst dann auftreten, wenn die Zugfestigkeit noch nicht erreicht wurde oder auch wenn der linear-elastische Bereich des Spannungs-Dehnungs-Diagramm noch nicht verlassen wurde.
Beispiel für eine dynamische Beanspruchung
Zum besseren Verständnis stellen wir uns eine Schraube vor, die am Gehäuse einer Rüttelmaschine, wie sie im Straßenbau eingesetzt wird, fixiert ist.

Die schwingende Belastung kann dann zu einem Bruch führen, selbst wenn die eigentliche Dehngrenze der Schraube noch nicht erreicht wurde.
Einflussfaktoren wie Korrosion/Rost oder Wärmeeinflüsse (Temperaturänderungen) können diesen Vorgang sogar noch beschleunigen.
Im Gegensatz zur statischen Beanspruchung äußert sich die dynamische Beanspruchung weitaus kritischer in Bezug auf die Werkstofffestigkeit.
Ein Sonderfall unter den dynamischen Beanspruchungen ist die schwingende Beanspruchung. Hier treten periodisch wiederkehrende Folgen von Beanspruchungsspitzen auf.
Darstellung einer dynamischen Beanspruchung im Diagramm
Je nach Lage der Mittelspannung, um welche die Beanspruchung schwankt, lassen sich folgenden
Fälle unterscheiden:
• wechselnde Beanspruchung mit Vorzeichenwechsel,
• schwingenden Beanspruchung mit geringem Vorzeichenwechsel,
• schwellende Beanspruchung ohne Vorzeichenwechsel
Alle drei Fälle sind in der nächsten Abbildung dargestellt.
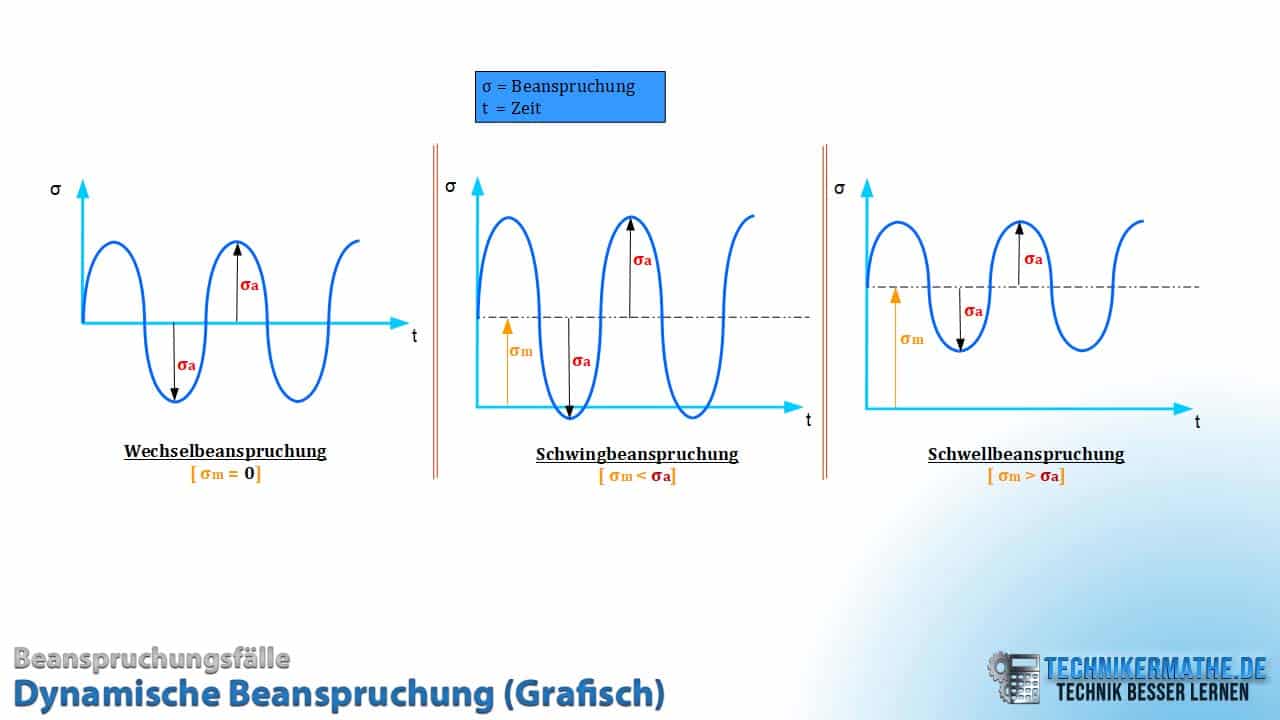
Wie du der Abbildung entnehmen kannst, verlaufen die beiden ersten Kurven von Minus nach Plus und von Plus nach Minus. Bei der letzten Kurve findet ebenfalls eine Zu- und Abnahme statt, jedoch sind die Werte immer im Plusbereich.
Spannungsformen: Ausschlagspannung & Mittelspannung
Liegt eine dynamische Beanspruchung vor, so können wir für unsere Berechnung nicht mehr die gültigen Werkstoffkennwerte einer statischen Beanspruchung heranziehen. Vielmehr nutzen wir die Ausschlagspannung ![]() und die Mittelspannung
und die Mittelspannung ![]() als zugehörige Größen um die Schwingbeanspruchung
als zugehörige Größen um die Schwingbeanspruchung ![]() und die Dauerfestigkeit
und die Dauerfestigkeit ![]() zu berechnen.
zu berechnen.
![]()
Kennzahlen:
 = Ausschlagspannung
= Ausschlagspannung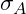 = maximal zulässige Ausschlagspannung
= maximal zulässige Ausschlagspannung
Dabei schwankt die Ausschlagspannung um die Mittelspannung herum und hilft die werkstoffspezifische Grenzspannung zu bestimmen.
Beide Größen, Ausschlagspannung und Mittelspannung, werden benötigt um die Schwingbeanspruchung eines Werkstoffes zu ermitteln.
![]()
Kennzahlen:
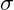 = Schwingbeanspruchung (Lastfall)
= Schwingbeanspruchung (Lastfall)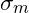 = Mittelspannung
= Mittelspannung = Ausschlagspannung
= Ausschlagspannung
Bei der Berechnung der Dauerfestigkeit ersetzen wir die Ausschlagspannung durch die maximal zulässige Ausschlagspannung.
![]()
Kennzahlen:
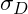 = Dauerfestigkeit (Lastfall)
= Dauerfestigkeit (Lastfall)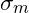 = Mittelspannung
= Mittelspannung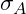 = maximal zulässige Ausschlagspannung
= maximal zulässige Ausschlagspannung
Sonderformen: Wechselbeanspruchung & Schwellbeanspruchung
Eine dynamische Beanspruchung verläuft nicht immer gleich. So treten ebenfalls
- Wechselbeanspruchungen mit Wechselfestigkeit und
- Schwellbeanspruchungen mit Schwellfestigkeit
auf. Diese werden formal anders erfasst, aus bisher.
![]()
![]()
Kennzahlen:
 = Wechselfestigkeit (Lastfall)
= Wechselfestigkeit (Lastfall)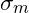 = Mittelspannung
= Mittelspannung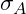 = maximal zulässige Ausschlagspannung
= maximal zulässige Ausschlagspannung
![]()
![]()
Kennzahlen:
 = Schwellfestigkeit (Lastfall)
= Schwellfestigkeit (Lastfall)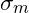 = Mittelspannung
= Mittelspannung = Ausschlagspannung
= Ausschlagspannung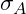 = maximal zulässige Ausschlagspannung
= maximal zulässige Ausschlagspannung
Nachdem wir uns mit dem Thema befasst haben, gehen wir in den kommenden Kurstexten intensiv auf die Wöhlerkurve und das Smith-Diagramm ein.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






