MA4 – Zwei Ebenen in Koordinatenform – Lagebeziehung

Für die Lagebeziehung von zwei Ebenen im Raum können wir drei Fälle unterscheiden. Zwei Ebenen im Raum können identisch sein, parallel zueinander liegen oder sich schneiden. Bei zwei sich schneidenden Ebenen können wir außerdem noch prüfen, ob die beiden Ebenen orthogonal (=rechtwinklig) zueinander sind.

In dieser Lerneinheit behandeln wir die Lagebeziehung von zwei Ebenen in Koordinatenform im Raum und wollen dir zeigen, wie du herausfinden kannst, ob die Ebenen identisch sind, parallel zueinander liegen oder sich schneiden.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs MA4 – Vektorrechnung auf Technikermathe.de

Für ein optimales Verständnis helfen dir drei anschauliche Rechenbeispiele zu dem Thema.

Lagebeziehungen zweier Ebenen

Identisch: Zwei Ebenen sind identisch, wenn die Richtungsvektoren der Ebenen linear voneinander abhängig sind und jeder Punkt der einen Ebene auch auf der anderen Ebene liegt. Damit gibt es unendlich viele Schnittgeraden.

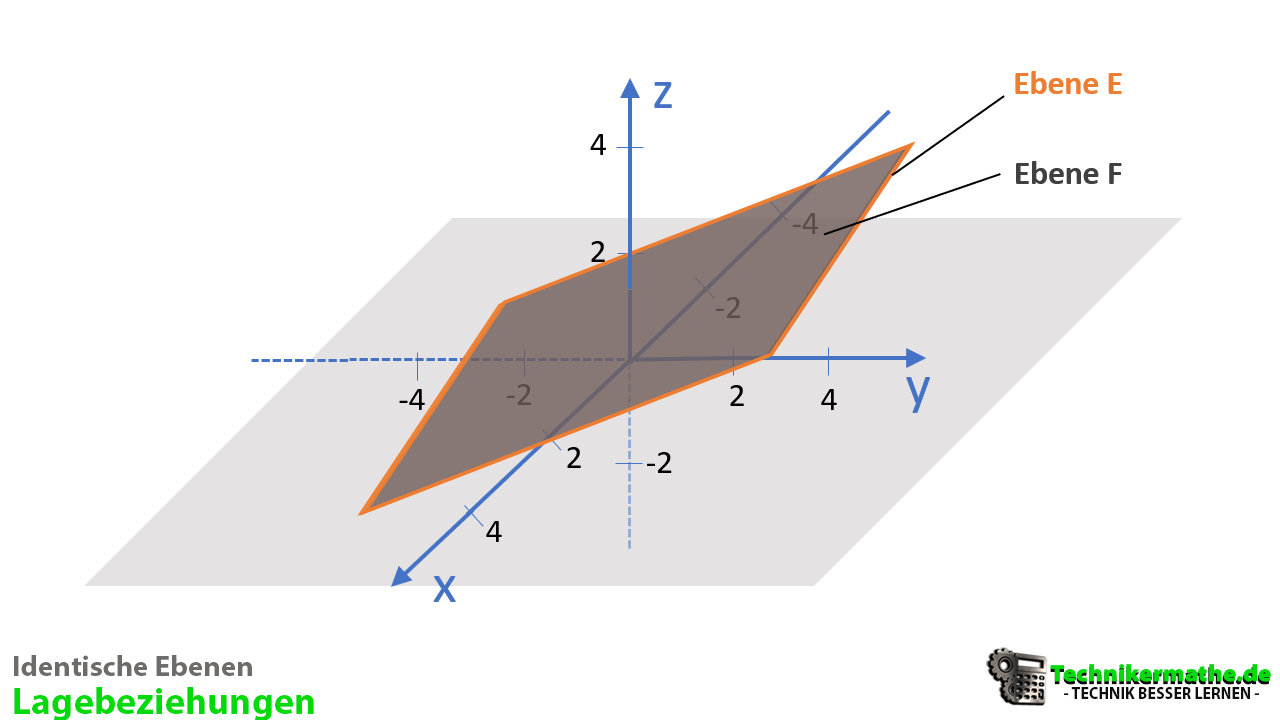
(Echt) parallel: Zwei Ebenen sind parallel zueinander, wenn die Richtungsvektoren der Ebenen linear voneinander abhängig sind und die Ebenen keinen gemeinsamen Schnittpunkt aufweisen (und damit auch keine Schnittgerade).

Schneidend: Zwei Ebenen schneiden sich, wenn sie genau eine Schnittgerade aufweisen, die alle gemeinsamen Schnittpunkt enthält. Die Richtungsvektoren der Ebenen sind linear unabhängig voneinander.

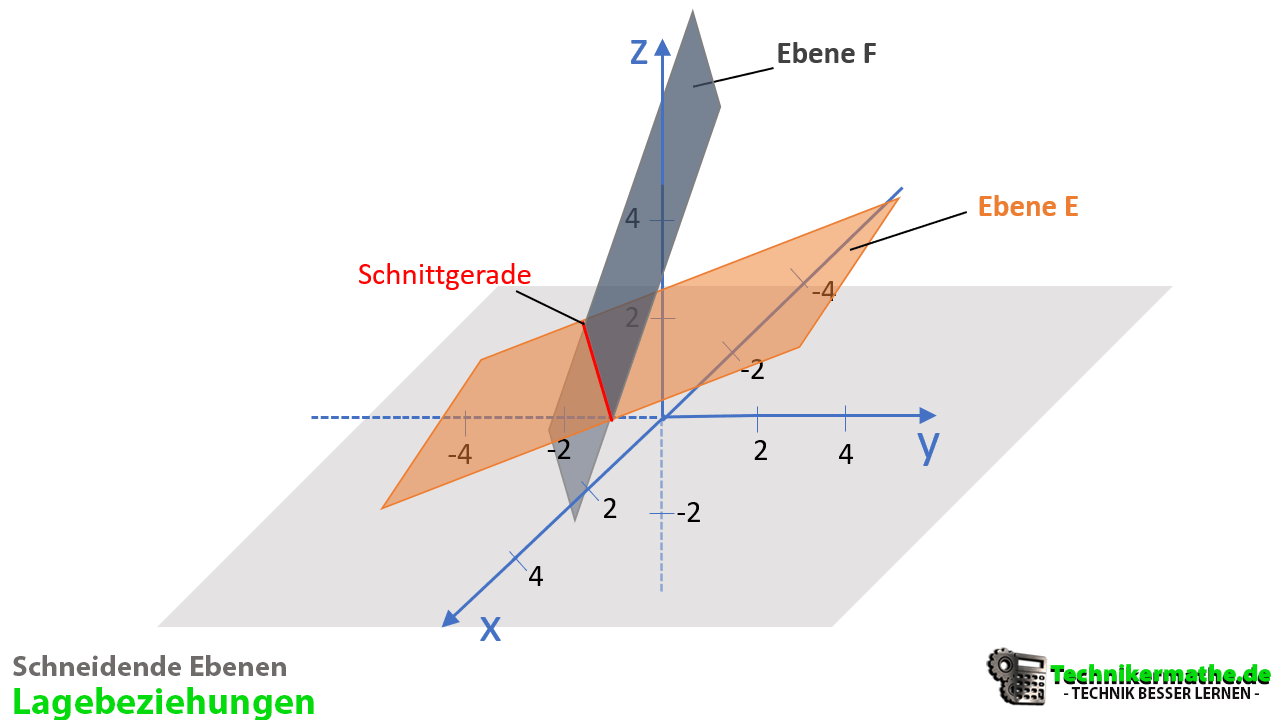
Orthogonal: Zwei Ebenen sind orthogonal, wenn sie genau eine Schnittgerade aufweisen, die alle gemeinsamen Schnittpunkt enthält und die Ebenen zusätzlich in einem 90°-Winkel zueinander stehen. Die Richtungsvektoren der Ebenen sind linear unabhängig voneinander.

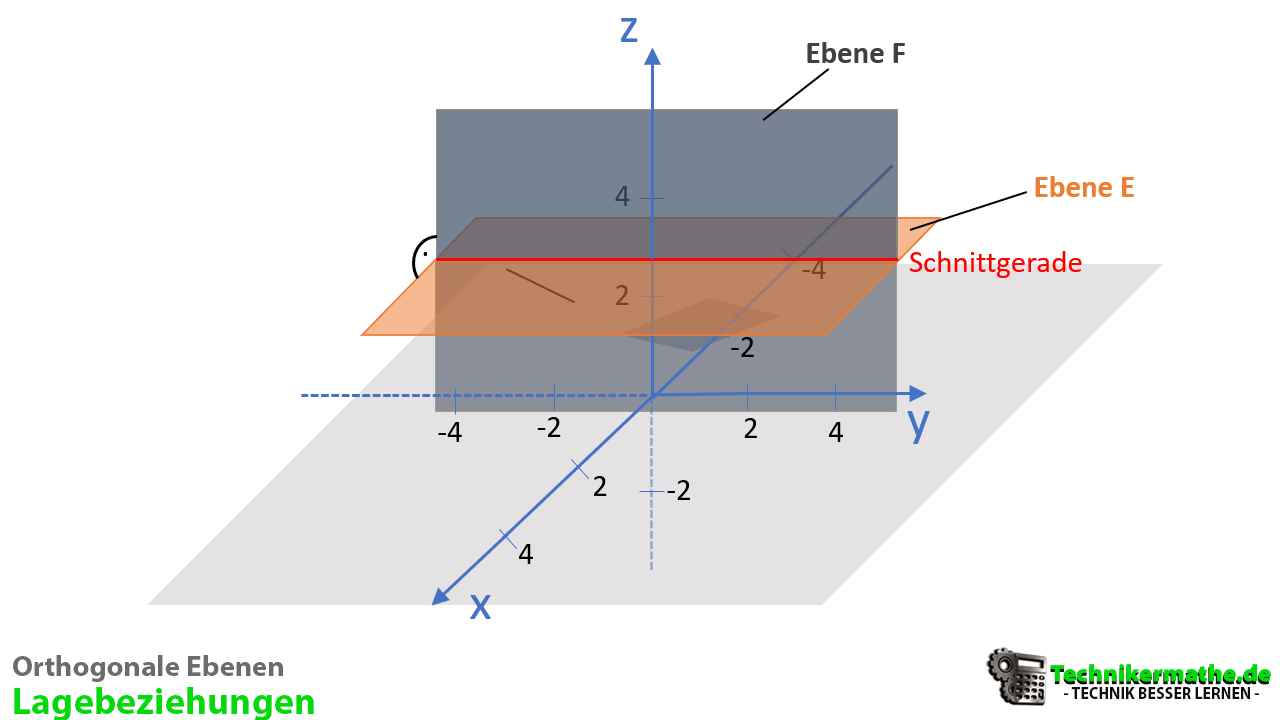
In den nachfolgenden Beispielen betrachten wir zwei Ebenen, die in Koordinatenform gegeben sind und wollen die Lagebeziehung der beiden Ebenen zueinander bestimmen.

In unserem Onlinekurs MA4-Vektorrechnung findest du zusätzlich den Fall, dass beide Ebenen in Parameterform gegeben sind sowie den Fall, dass eine Ebene in Parameterform und eine Ebene in Koordinatenform gegeben ist.

Wir zeigen dir in unserem Onlinekurs MA4-Vektorrechnung außerdem wie du die Schnittgerade bei zwei sich schneidenden Ebenen bestimmst.

Vorgehensweise: Zwei Ebenen in Koordinatenform

Gegeben seien die zwei Ebenen E und F in Koordinatenform. Zunächst liest du aus der Koordinatenform der Ebenen die beiden Normalenvektoren n_E und n_F ab.
Als nächstes überprüfst du, ob die beiden Normalenvektoren Vielfache voneinander sind, indem du die Linearkombination aufstellst:

$\vec{n}_E = \lambda \vec{n}_F$

Es gibt nun drei Fälle, die unterschieden werden müssen:

Sind die beiden Normalenvektoren Vielfache voneinander und sind zusätzlich die beiden Koordinatenformen der Ebenen Vielfache voneinander, so sind die beiden Ebenen identisch. Dies überprüfst du, indem du die Linearkombination aus den Koeffizienten d aufstellst:

$d_E = \lambda \cdot d_F$

Resultiert derselbe Wert für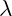 $\lambda$ wie in 2., so sind die beiden Ebenen identisch. Damit gibt es unendlich viele Schnittgeraden.
Sind die beiden Normalenvektoren Vielfache voneinander, aber die beiden Koordinatenformen der beiden Ebenen nicht, so sind die beiden Ebenen echt parallel. Damit gibt es keine Schnittgerade.
Sind die beiden Normalenvektoren keine Vielfache voneinander, so schneiden sich die beiden Ebenen. Damit gibt es genau eine Schnittgerade. Sind die beiden Normalenvektoren dann noch senkrecht zueinander, sind die beiden Ebenen orthogonal. Dies überprüfst du, indem du das Skalarprodukt der beiden Normalenvektoren n_E und n_F berechnest. Ist dieses gleich Null, so sind die beiden Vektoren senkrecht zueinander und damit auch die beiden Ebenen E und F.

Betrachten wir als nächstes drei Beispiele, um die obigen drei Fälle einmal abzubilden.

Beispiel 1: Lagebeziehung zweier Ebenen in Koordinatenform

Beispiel!

Gegeben sei die Ebene $E: 4x -6y -2z = 4$ und die Ebene $F: -2x + 3y + z = -2$ .

Welche Lagebeziehung zwischen den beiden Ebenen ist gegeben?

Um herauszufinden, wie die beiden Ebenen zueinander liegen, betrachten wir die beiden Normalenvektoren und prüfen, ob diese linear abhängig sind. Die Normalenvektoren können wir einfach aus der Koordinatenform ablesen:

$ax + by + cz = d$

$\vec{n} = \left( \begin{array}{c} a \\ b \\ c \end{array}\right)$

Die beiden Normalenvektoren lauten:

$\vec{n}_E = \left( \begin{array}{c} 4 \\ -6 \\ -2 \end{array}\right)$

$\vec{n}_F = \left( \begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$

Als nächstes stellen wir die Linearkombination aus beiden Vektoren auf:

$\vec{n}_E = \lambda \cdot \vec{n}_F$

$\left( \begin{array}{c} 4 \\ -6 \\ -2 \end{array}\right) = \lambda \cdot \left( \begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$

Wir stellen das lineare Gleichungssystem auf und berechnen $\lambda$ :

(1) $4 = -2 \lambda$ $\rightarrow \lambda = -2$

(2) $-6 = 3 \lambda$ $\rightarrow \lambda = -2$

(3) $-2 = 1 \lambda$ $\rightarrow \lambda = -2$

Da $\lambda$ für alle drei Gleichungen identisch ist, sind die beiden Normalenvektoren linear abhängig voneinander (=vielfache voneinander). Die beiden Ebenen E und F sind nun entweder identisch oder echt parallel. Um das herauszufinden, müssen wir uns als nächstes den Koeffizienten d der Koordinatenformen anschauen. Wir wissen nun, dass der Normalenvektor $\vec{n}_E$ resultiert, wenn wir den Normalenvektor $\vec{n}_F$ mit (-2) multiplizieren. Wir wollen nun schauen, ob derselbe Zusammenhang auch zwischen den Koeffizienten d besteht:

$E: 4x -6y -2z = 4$

$F: -2x + 3y + z = -2$

$d_E = \lambda \cdot d_F$

$4 = \lambda \cdot (-2)$

$\lambda = -2$

Da für $\lambda = -2$ resultiert, sind die beiden Ebenen identisch!

Beispiel 2: Lagebeziehung zweier Ebenen

Beispiel!

Gegeben sei die Ebene $E: 3x - 0,5y - z = 4$ und die Ebene $F: 6x - y - 2 = 6$ .

Welche Lagebeziehung zwischen den beiden Ebenen ist gegeben?

$\vec{n}_E = \left( \begin{array}{c} 3 \\ -0,5 \\ -1 \end{array}\right)$

$\vec{n}_F = \left( \begin{array}{c} 6 \\ -1 \\ -2 \end{array}\right)$

Als nächstes stellen wir die Linearkombination aus beiden Vektoren auf:

$\vec{n}_E = \lambda \cdot \vec{n}_F$

$\left( \begin{array}{c} 3 \\ -0,5 \\ -1 \end{array}\right) = \lambda \cdot \left( \begin{array}{c} 6 \\ -1 \\ -2 \end{array}\right)$

Wir stellen das lineare Gleichungssystem auf und berechnen $\lambda$ :

(1) $3 = 6 \lambda$ $\rightarrow \lambda = 0,5$

(2) $-0,5 = -1 \lambda$ $\rightarrow \lambda = 0,5$

(3) $-1 = -2 \lambda$ $\rightarrow \lambda = 0,5$

Da $\lambda$ für alle drei Gleichungen identisch ist, sind die beiden Normalenvektoren linear abhängig voneinander (=vielfache voneinander). Die beiden Ebenen E und F sind nun entweder identisch oder echt parallel. Um das herauszufinden, müssen wir uns als nächstes den Koeffizienten d der Koordinatenformen anschauen. Wir wissen nun, dass der Normalenvektor $\vec{n}_E$ resultiert, wenn wir den Normalenvektor $\vec{n}_F$ mit 0,5 multiplizieren. Wir wollen nun schauen, ob derselbe Zusammenhang auch zwischen den Koeffizienten d besteht:

$E: 3x -0,5y -z = 4$

$F: 6x - y - 2z = 6$

$4 = \lambda 6$

$\lambda = \frac{2}{3}$

Da $\lambda$ nicht 0,5 entspricht, sind die beiden Ebenen nicht identisch sondern echt parallel zueinander.

Beispiel 3: Lagebeziehung zweier Ebenen

Beispiel!

Gegeben sei die Ebene $E: 4x -6y - 2z = 4$ und die Ebene $F: -2x - 3y + z = 2$ .

Welche Lagebeziehung zwischen den beiden Ebenen ist gegeben?

$\vec{n}_E = \left( \begin{array}{c} 4 \\ -6 \\ -2 \end{array}\right)$

$\vec{n}_F = \left( \begin{array}{c} -2 \\ -3 \\ 1 \end{array}\right)$

Als nächstes stellen wir die Linearkombination aus beiden Vektoren auf:

$\vec{n}_E = \lambda \cdot \vec{n}_F$

$\left( \begin{array}{c} 4 \\ -6 \\ -2 \end{array}\right) = \lambda \cdot \left( \begin{array}{c} -2 \\ -3 \\ 1 \end{array}\right)$

Wir stellen das lineare Gleichungssystem auf und berechnen $\lambda$ :

(1) $4 = -2 \lambda$ $\rightarrow \lambda = -2$

(2) $-6 = -3 \lambda$ $\rightarrow \lambda = 2$

(3) $-2 = 1 \lambda$ $\rightarrow \lambda = -2$

$\lambda$ ist nicht für alle drei Gleichungen identisch, damit sind die beiden Normalenvektoren linear unabhängig voneinander (= keine vielfache voneinander). Die beiden Ebenen E und F schneiden sich und es existiert eine Schnittgerade.

Wie die Schnittgerade bestimmt wird, zeigen wir dir in einem späteren Abschnitt dieses Kapitels.

Wir können nun noch überprüfen, ob die beiden Ebenen E und F senkrecht zueinander sind. Dazu bilden wir das Skalarprodukt aus den beiden Normalenvektoren:

$\vec{n}_E \cdot \vec{n}_F = 0$ Ebenen sind orthogonal zueinander

$\vec{n}_E \cdot \vec{n}_F \neq 0$ Ebenen sind nicht orthogonal zueinander

Wir überprüfen:

$\left( \begin{array}{c} 4 \\ -6 \\ -2 \end{array}\right) \cdot \left( \begin{array}{c} -2 \\ -3 \\ 1 \end{array}\right) = 4 \cdot (-2) + (-6) \cdot (-3) + (-2) \cdot 1 = 8$

Das Skalarprodukt ist ungleich Null, damit sind die beiden sich schneidenden Ebenen E und F nicht orthogonal zueinander.

Was gibt es noch bei uns?

Tausende interaktive Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++