Wir wollen uns in diesem Abschnitt mal anschauen, wie Bruchgleichungen mit der Faktorzerlegung gelöst werden können. Ziel ist es hierbei mehrere Brüche mittels Faktorzerlegung auf einen gemeinsamen Nenner zu bringen. Danach kann der Bruch ganz einfach nach der gesuchten Variable aufgelöst werden.
Dieses Vorgehen ist dann sinnvoll, wenn mehrere Brüche mit unterschiedlichen Nennern gegeben sind.
Schauen wir uns dazu mal ein Beispiel an:
Löse nach x auf! Wende die Faktorzerlegung an!
Vorgehensweise: Bruchgleichung mittels Faktorzerlegung
Wir wollen diese Bruchgleichung lösen. Dazu müssen wir die Brüche zusammenfassen. Sinnvoll ist es also erstmal einen gemeinsamen Nenner zu finden, den Hauptnenner. Hier können wir die Faktorzerlegung anwenden.
Dazu wird nun jeder Nenner faktorisiert. Schauen wir uns als Beispiel mal den 1. Nenner an:
Diesen können wir faktorisieren, indem wir den größten gemeinsamen Faktor ausklammern:
Wir haben hier nun zwei Faktoren gegeben. Einmal und einmal
. So gehen wir für jeden Nenner vor und tragen die Faktoren in einer Tabelle ab. Dabei erhält jeder Nenner eine eigene Zeile.
Gleiche Faktoren werden dabei untereinander geschrieben. Die folgende Tabelle zeigt das Vorgehen:
| 1. Nenner | 2 | (2-x) | ||
| 2. Nenner | 4 | (1-x) | ||
| 3. Nenner | (2-x) | |||
| 4. Nenner | 2 | (1-x) | ||
| Hauptnenner: | 2 | (2-x) | 4 | (1-x) |
Du beginnst mit dem 1. Nenner und den beiden Faktoren 2 und (2-x) und fügst dann die Faktoren 4 und (1-x) des 2. Nenners als neue Spalten an. Der Nenner 3 mit (2-x) kann nicht mehr faktorisiert werden und ist bereits gegeben, also schreibst du ihn in die Spalte, in welcher er bereits vorkommt (3. Spalte). Nenner 4 setzt sich aus 2 und (1-x) zusammen. Beide Faktoren sind schon in der Tabelle gegeben, also werden sie in die dazugehörige Spalte geschrieben.
Wichtig: Gleiche Faktoren werden untereinander geschrieben, ungleiche Faktoren erhalten eine eigene Spalte!
Der Hauptnenner ist dann nichts anders als die Faktoren der Spalte:
Dort wo sich nun innerhalb der Tabelle Lücken gegeben haben, müssen die Zähler mit den dort fehlenden Faktoren multipliziert werden.
Der Zähler der 1. Bruchs muss also mit 4(1-x) erweitert werden:
Der Zähler der 2. Bruchs muss also mit 2(2-x) erweitert werden:
Der Zähler der 3. Bruchs muss also mit 2 · 4 · (1-x) = 8(1-x) erweitert werden:
Der Zähler der 4. Bruchs muss also mit (2-x)4 erweitert werden:
Wir haben nun alle Brüche auf einen gemeinsamen Hauptnenner gebracht:
Multiplikation beider Seiten mit dem Hauptnenner, damit dieser wegfällt:
Klammern auflösen:
Nach x auflösen:
Setzen wir nun in die obige Bruchgleichung x = 16/18 ein, so erhalten wir auf beiden Seiten:
Damit ist die Bruchgleichung erfüllt und das Ergebnis ermittelt. x muss also 16/18 annehmen, damit beide Seiten gleich sind.
- Faktorzerlegung der Nenner und Eintragung in eine Tabelle
- Bestimmung des Hauptnenners aus den Spalten der Tabelle.
- Bestimmung der neuen Zähler aus den Lücken der Tabelle.
- Elimination des Hauptnenners.
- Auflösen nach x.
Was gibt es noch bei uns?
Was ist Technikermathe.de?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Interaktive Übungsaufgaben
Quizfrage 1
Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?
Auszüge aus unserem Kursangebot
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ENT3 (Energetische Berechnungen) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team


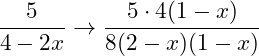
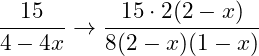
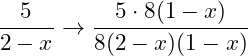
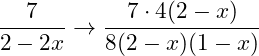
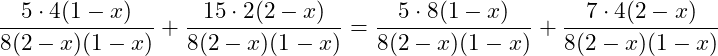

![[MA2] Bruchgleichung mittels Faktorzerlegung lösen 4 Trainingsbereich](https://technikermathe.de/wp-content/uploads/2020/01/Trainingsbereich.png)





