PH1 – Kosinus bei rechtwinkligen Dreiecken

Der Kosinus eines Winkels ist definiert als Ankathete geteilt durch die Hypotenuse. Du kannst den Winkel in einem rechtwinkligen Dreieck mittels Kosinus berechnen, wenn die Ankathete zum betrachteten Winkel und die Hypotenuse gegeben sind. Mittels Kosinus kann ebenfalls eine Seite berechnet werden, wenn der Winkel und die Ankathete oder Hypotenuse gegeben sind.

In dieser Lerneinheit zeigen wir dir ausführlich, wie du den Kosinus bei rechtwinkligen Dreiecken anwendest. Dabei erlernst sehr übersichtlich und einfach, wie du mit Hilfe des Kosinus eine Seite oder einen Winkel in einem rechtwinkligen Dreieck berechnest.

Für ein optimales Verständnis helfen dir ein Videoclip und vier ausführlich gelöste Beispiele. Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH1 – Grundlagen der Physik.

Kosinus bei rechtwinkligen Dreiecken – Grundlagen

Kosinus anwenden - Kosinus bei rechtwinkligen Dreiecken — Kosinus anwenden – Kosinus bei rechtwinkligen Dreiecken

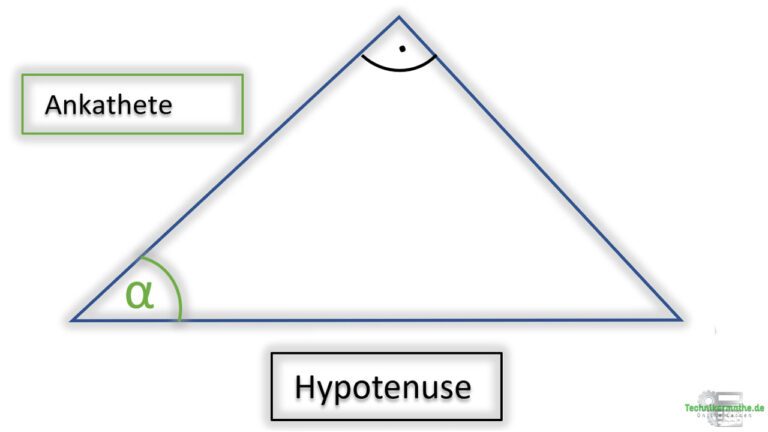
Der Kosinus eines spitzen Winkels wird berechnet, indem der Quotient aus der Länge der Ankathete und der Hypotenuse gebildet wird:

$\cos(\alpha) = \dfrac{\text{Ankathete}}{\text{Hypotenuse}}$ Kosinus

Sind in einem rechtwinkligen Dreieck zwei der drei obigen Größen gegeben, so kannst du die dritte Größe mit dem Kosinus berechnen.

Schauen wir uns zunächst einmal an, wie die obige Gleichung nach der Ankathete, Hypotenuse und nach dem Winkel $\alpha$ aufgelöst wird.

Kosinus bei rechtwinkligen Dreiecken – Ankathete

Ist in der Aufgabe die Hypotenuse und der Winkel $\alpha$ gegeben und du sollst die Ankathete berechnen, dann musst du die obige Gleichung nach der Ankathete auflösen:

$\text{Ankathete} = \text{Hypotenuse} \cdot \cos(\alpha)$ Berechnung der Ankathete

Kosinus bei rechtwinkligen Dreiecken – Hypotenuse

Ist in der Aufgabe die Ankathete und der Winkel $\alpha$ gegeben und du sollst die Hypotenuse berechnen, dann musst du die obige Gleichung nach der Hypotenuse auflösen:

$\text{Hypotenuse} = \dfrac{\text{Ankathete}}{ \cos(\alpha) }$ Berechnung der Hypotenuse

Kosinus bei rechtwinkligen Dreiecken – Winkel

Wenn du den Winkel berechnen sollst und es ist die Ankathete und die Hypotenuse gegeben, dann musst du die obige Gleichung nach dem Winkel $\alpha$ auflösen. Dazu benötigst du den Arkuskosinus ( $\cos^{-1}$ bzw. $\arccos$ ).

Der Arkuskosinus ist die Umkehrfunktion des Kosinus. Wendest du diese Umkehrfunktion auf $\cos(\alpha)$ an, so fällt der Kosinus weg und es bleibt der Winkel $\alpha$ stehen. Du darfst aber nicht vergessen den Arkuskosinus auf der anderen Seite der Gleichung anzuwenden.

Wir betrachten die obige Gleichung und wenden auf beiden Seiten den Arkuskosinus an:

$\cos^{-1} (\cos(\alpha)) = \cos^{-1} (\dfrac{\text{Ankathete}}{\text{Hypotenuse}})$

Auf der linken Seite fällt der Kosinus einfach weg und es verbleibt der Winkel. Auf der rechten Seite bleibt der Arkuskosinus stehen:

$\alpha = \cos^{-1}(\dfrac{\text{Ankathete}}{\text{Hypotenuse}})$ Berechnung des Winkels mittels Kosinus

Merk’s dir!

Zur Berechnung einer Seite oder eines Winkels mittels Kosinus, müssen also zwei der drei Größe innerhalb der Gleichung gegeben sein.

Videoclip: Winkel mit Kosinus berechnen

Damit du fit für die Prüfung bist, schau dir die nachfolgenden Beispiele zum Thema Kosinus bei rechtwinkligen Dreiecken an und versuche diese zunächst selbstständig zu lösen.

Beispiele: Kosinus anwenden

Schauen wir uns dazu mal die nachfolgenden Beispiele an, in denen wir mittels Kosinus die Hypotenuse, den Winkel und die Ankathete eines rechtwinkligen Dreiecks bestimmen wollen.

Beispiel 1: Berechnung der Hypotenuse mittels Kosinus

Aufgabenstellung

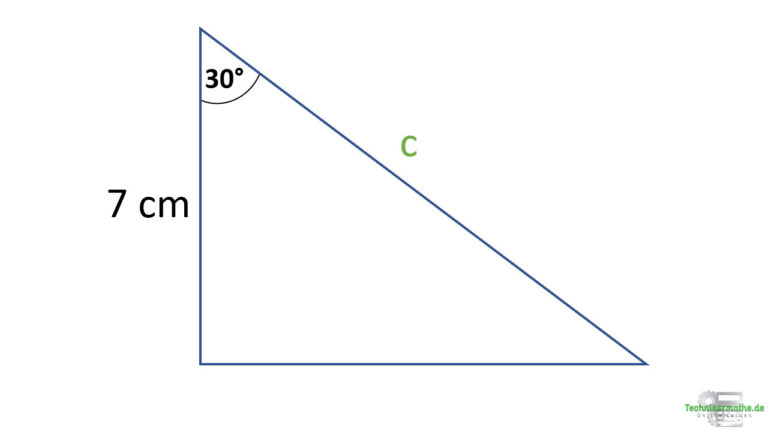
Gegeben sei das obige rechtwinklige Dreieck mit dem Spitzen Winkel α = 30° und der Seitenlänge von 7 cm. Berechne die Seite c!

Lösung

Zunächst müssen wir herausfinden, welche Größen wir gegeben haben. Wir haben zum einen den spitzen Winkel mit 30° gegeben und zum anderen die Seite am spitzen Winkel – die Ankathete. Gesucht wird die Seite gegenüber vom rechten Winkel – die Hypotenuse.

Gegeben: Spitzer Winkel, Ankathete

Gesucht: Hypotenuse

Formel: Kosinus

Danach schauen wir uns die Kosinus-Gleichung aufgelöst nach der gesuchte Hypotenuse an:

$\text{Hypotenuse} = \dfrac{\text{Ankathete}}{ \cos(\alpha) }$

Wir setzen die gegebenen Werte ein:

$c = \dfrac{7 cm}{\cos(30^{\circ})}$

Das Ergebnis ist:

$c = 8,08 cm$

Die Länge der Seite c für das obige Dreieck beträgt 8,08 cm.

Beispiel 2: Berechnung des Winkels mittels Kosinus

Aufgabenstellung

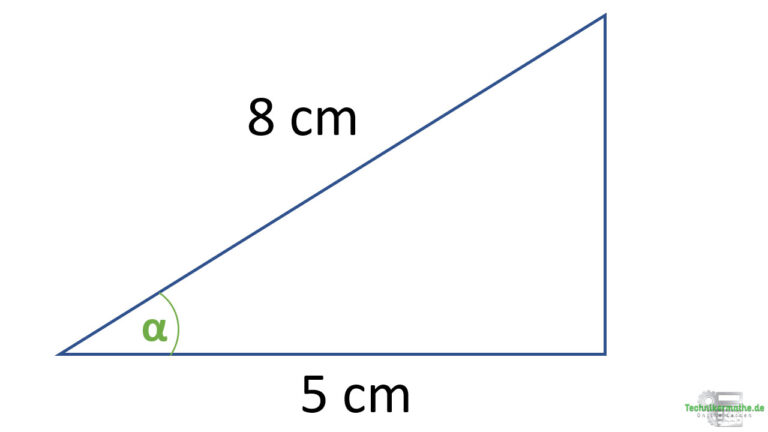
Gegeben sei das obige rechtwinklige Dreieck mit den beiden Seitenlängen 5 cm und 8 cm. Berechne den Winkel α!

Lösung

In diesem Beispiel sind zwei Seitenlängen gegeben aus denen der Winkel berechnet werden soll. Zunächst müssen wir festlegen, welche Seiten in Bezug auf den Winkel α gegeben sind. Die Seitenlänge mit 8 cm liegt gegenüber vom rechten Winkel, hier ist also die Länge der Hypotenuse gegeben. Die Seitenlänge 5 cm liegt am betrachteten Winkel $\alpha$ und ist damit die Länge der Ankathete.

Gegeben: Ankathete, Hypotenuse

Gesucht: Winkel

Formel: Kosinus

Wir wenden hier den Kosinus an, weil dieser alle relevanten Größe enthält. Wir suchen den Winkel $\alpha$ , deswegen verwenden wir die Kosinus-Gleichung aufgelöst nach dem Winkel:

$\alpha = \cos^{-1}(\frac{\text{Ankathete}}{\text{Hypotenuse}})$

Einsetzen der gegebenen Werte:

$\alpha = \cos^{-1} (\dfrac{5 cm}{8 cm})$

Der Taschenrechner liefert das Ergebnis:

$\alpha = 51,32 ^{\circ}$

Der Winkel $\alpha$ des obigen Dreiecks beträgt 51,32°.

Beispiel 3: Berechnung der Ankathete mittels Kosinus

Aufgabenstellung

Gegeben sei das obige rechtwinklige Dreieck mit der Seitenlängen 12 cm und dem Winkel von 55°! Berechne die Seite b!

Lösung

Zunächst müssen wir herausfinden, welche Größen wir gegeben haben. Wir haben zum einen den spitzen Winkel mit 55° gegeben und zum anderen die Seite gegenüber vom rechten Winkel- die Hypotenuse. Gesucht wird die Seite am spitzen Winkel, die Ankathete.

Gegeben: Spitzer Winkel, Hypotenuse

Gesucht: Ankathete

Formel: Kosinus

Danach schauen wir uns die Kosinus-Gleichung aufgelöst nach der gesuchte Ankathete an:

$\text{Ankathete} = \text{Hypotenuse} \cdot \cos(\alpha)$

Wir setzen die gegebenen Werte ein:

$b = 12 cm \cdot \cos(55^{\circ})$

Das Ergebnis ist:

$b = 6,88 cm$

Die Länge der Seite b für das obige Dreieck beträgt 6,88 cm.

Beispiel 4: Seifenkistenrennen – Strecke berechnen

Aufgabenstellung

Gegeben sei die Strecke eines Seifenkistenrennens. Die ersten 35 Meter weist die Strecke eine Steigung von 17° auf, die restlichen 120 Meter eine Steigung von 6°.

Welcher horizontale Abstand ist zwischen Start und Ziel gegeben?

Lösung

Wir müssen hier rechtwinklige Dreieck so konstruieren, dass wir die horizontale Strecke berechnen können:

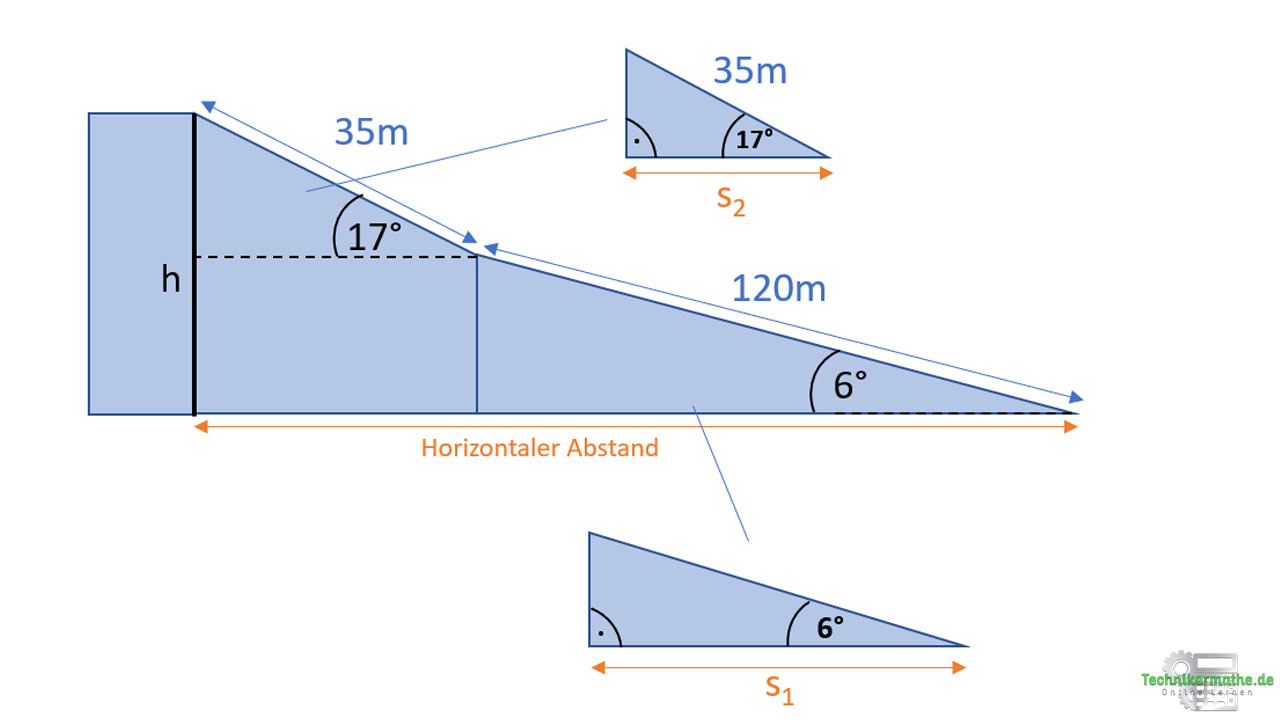
Wir berechnen zunächst die Strecke s₁ mittels Kosinus, da s₁ die Ankathete und 120m die Hypotenuse darstellen:

$\cos(6^{\circ}) = \dfrac{s_1}{120m}$

Wir lösen nach der gesuchten Seite auf:

$\cos(6^{\circ}) = \dfrac{s_1}{120m}$ | $\cdot 120 m$

$\cos(6^{\circ}) \cdot 120 m = s_1$

Es ergibt sich dann:

$s_1 = 119,34 m$

Als nächstes betrachten wir die Teilstrecke 2 und wenden auch hier den Kosinus an:

$\cos(17^{\circ}) = \dfrac{s_2}{35m}$ | $\cdot 35 m$

$\cos(17^{\circ}) \cdot 35 m = s_2$

Es ergibt sich dann:

$s_2 = 33,47m$

Die gesamte Strecke beträgt:

$s = s_1 + s_2 = 119,34 m + 33,47 m = 152,81 m$

Tausende interaktive Übungsaufgaben

Übungsbereich

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++