HM1 – Bestimmte Integrale [Definition, Formel, Beispiele]

Ein bestimmtes Integral berechnet den Flächeninhalt zwischen einer Funktion $f (x)$ und der $x$ -Achse im Intervall .

In dieser Lerneinheit betrachten wir die bestimmte Integration und zeigen dir, wie du den Flächeninhalt zwischen Funktion und x-Achse berechnest.

Für ein optimales Verständnis helfen dir zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs HM1 – Höhere Mathematik 1.

In dieser Lerneinheit behandeln wir die bestimmte Integration.

Was sind bestimmte Integrale?

Mithilfe der bestimmten Integration wird die Fläche zwischen der gegebenen Funktion und er x-Achse im Intervall [a,b] berechnet.

Die Schreibweise für ein bestimmtes Integral ist:

Bestimmtes Integral: Fläche

$A = \int_{a}^{b} f(x) \,dx$

mit

$A$ Fläche zwischen Funktion und x-Achse

$a$ untere Grenze

$b$ obere Grenze

$f(x)$ Funktion, die integriert wird

$dx$ zeigt an, dass nach $x$ integriert wird.

Unterschied: Bestimmtes und unbestimmtes Integral

Art der Integration	Symbol	Bedeutung
Unbestimmtes Integral	$\int f(x) \,dx$	Liefert eine Stammfunktion F(x), also eine Funktion, deren Ableitung wieder f(x) ergibt. Enthält die Konstante C, da unendlich viele Stammfunktionen möglich sind.
Bestimmtes Integral	$\int_{a}^{b} f(x) \,dx$	Berechnet die Fläche zwischen der Funktion f(x) und der x-Achse im Intervall [a,b]. Führt zu einem konkreten Zahlenwert.

Bestimmtes Integral: Berechnung

Die Berechnung basiert auf dem Hauptsatz der Differential- und Integralrechnung:

Hauptsatz der Differential- und Integralrechnung

$A = \int_{a}^{b} f(x) \,dx = F(b) - F(a)$

Hierbei handelt es sich um die Fläche der Funktion f(x) im Intervall [a,b]. Nach der Integration werden die Grenzen eingesetzt und voneinander subtrahiert. Man setzt zuerst die obere und dann die untere Grenze ein.

Beispiel 1: Flächeninhalt (lineare Funktion)

Aufgabenstellung

$f(x) = 2x$

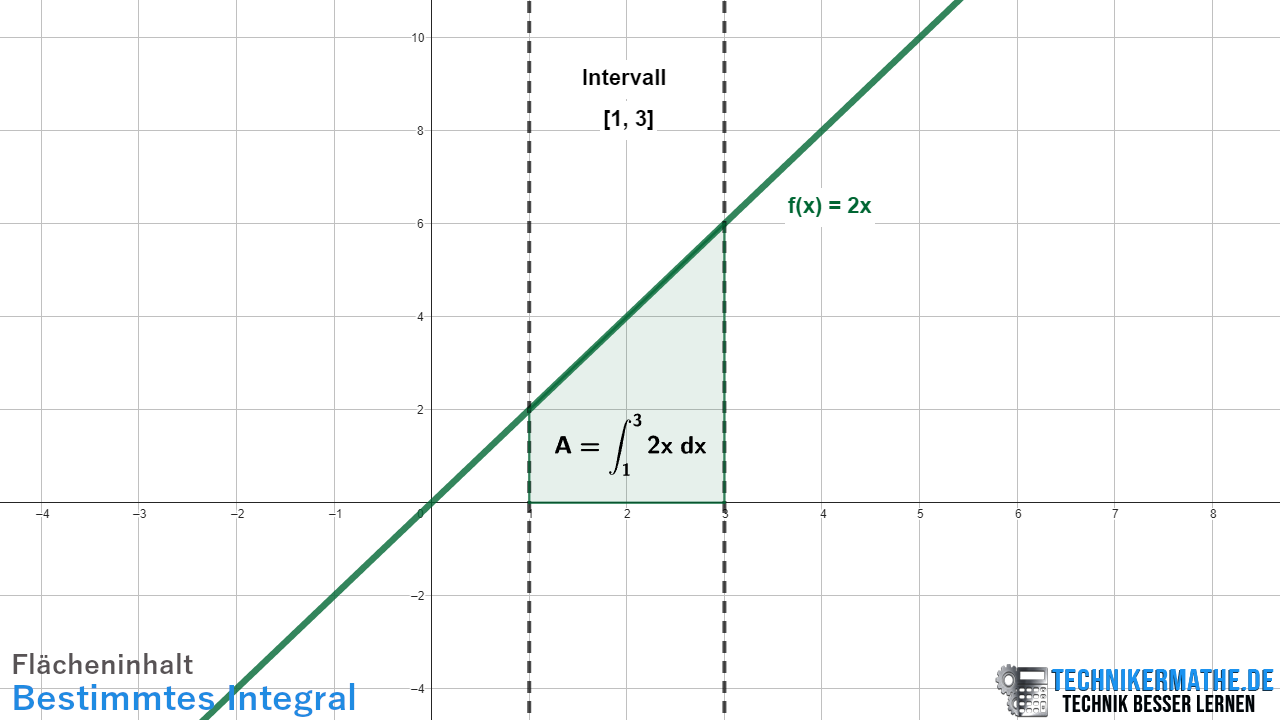
Berechne die Fläche zwischen der Funktion und der x-Achse im Intervall [1,3].

Schritt 1: Stammfunktion bestimmen

Um die Fläche zu bestimmen, müssen wir dies gegebene Funktion f(x) integrieren und die Grenzen des Intervalls berücksichtigen:

$A = \int_1^3 2x \,dx = 2 \int_1^3 x \, dx = 2 \cdot [\frac{1}{2} x^2]_1^3$

Es wird zunächst integriert. Nach der Integration werden die Grenzen an eckige Klammern geschrieben und dann in die Stammfunktion eingesetzt.

Jetzt setzen wir $x = 3$ (obere Grenze) und $x = 1$ (untere Grenze) ein und subtrahieren:

$F(b) - F(a) = 2 \cdot [\frac{1}{2} 3^2 - \frac{1}{2} 1^2] = 2 \cdot \frac{8}{2} = 8$

Das bestimmte Integral ergibt also 8 Flächeneinheiten. Flächeneinheiten sind m² und Vielfache davon, je nachdem was in der Aufgabenstellung an Längeneinheiten (m, mm, …) gegeben sind.

In der obigen Grafik siehst du die Funktion f(x) = 2x eingezeichnet. Mittels Integration über die Grenzen 1 bis 3 haben wir den Flächeninhalt zwischen der Funktion und der x-Achse im Intervall [1, 3] bestimmt. Wir können den Flächeninhalt auch aus der Grafik berechnen:

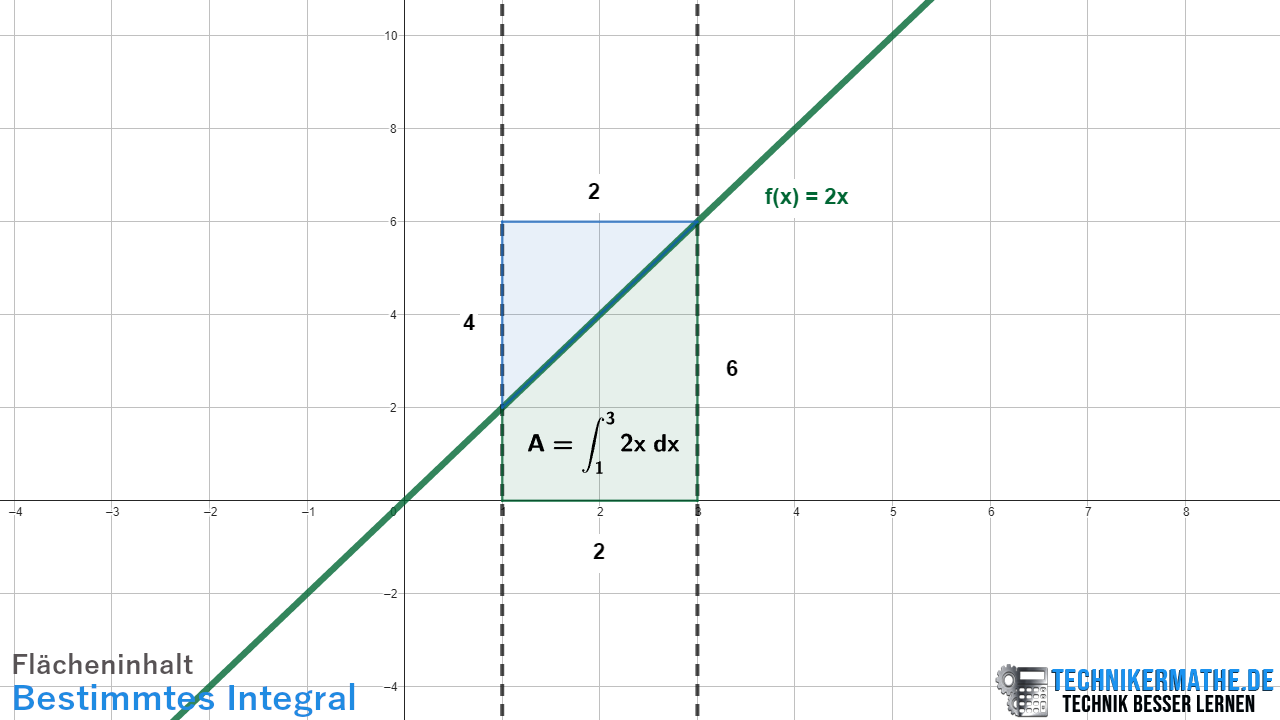
In der obigen Grafik kannst du den Flächeninhalt bestimmen, indem du zunächst das gesamte Rechteck berechnest (6 · 2 = 12). Danach berechnest du die Fläche des Dreiecks (1/2 · 2 · 4 = 4). Du ziehst dann das Dreieck von dem gesamten Rechteck ab, so dass nur die grüne Fläche unterhalb der Funktion verbleibt (12 – 4 = 8).

In diesem Beispiel mit einer linearen Funktion können wir die Fläche problemlos auch aus der Grafik berechnen. Bei höheren Funktionen ist dies nicht mehr möglich, da sich hier Parabeln und Kurven ergeben, für die wir den Flächeninhalt nicht mehr aus der Grafik berechnen können. Deswegen führen wir in solchen Fälle die bestimmte Integration durch.

Flächeninhalt und bestimmte Integration

Ein bestimmtes Integral beschreibt oft den Flächeninhalt unter einer Funktion f(x) zwischen zwei Grenzen.

Wenn f(x) oberhalb der x-Achse liegt, ergibt das Integral die positive Fläche.
Wenn f(x) unterhalb der x-Achse liegt, ergibt das Integral eine negative Fläche.
Liegt die Funktion teils über, teils unter der x-Achse, müssen die Flächen separat betrachtet werden.

Beispiel 2: Flächeninhalt (quadratische Funktion)

Aufgabenstellung

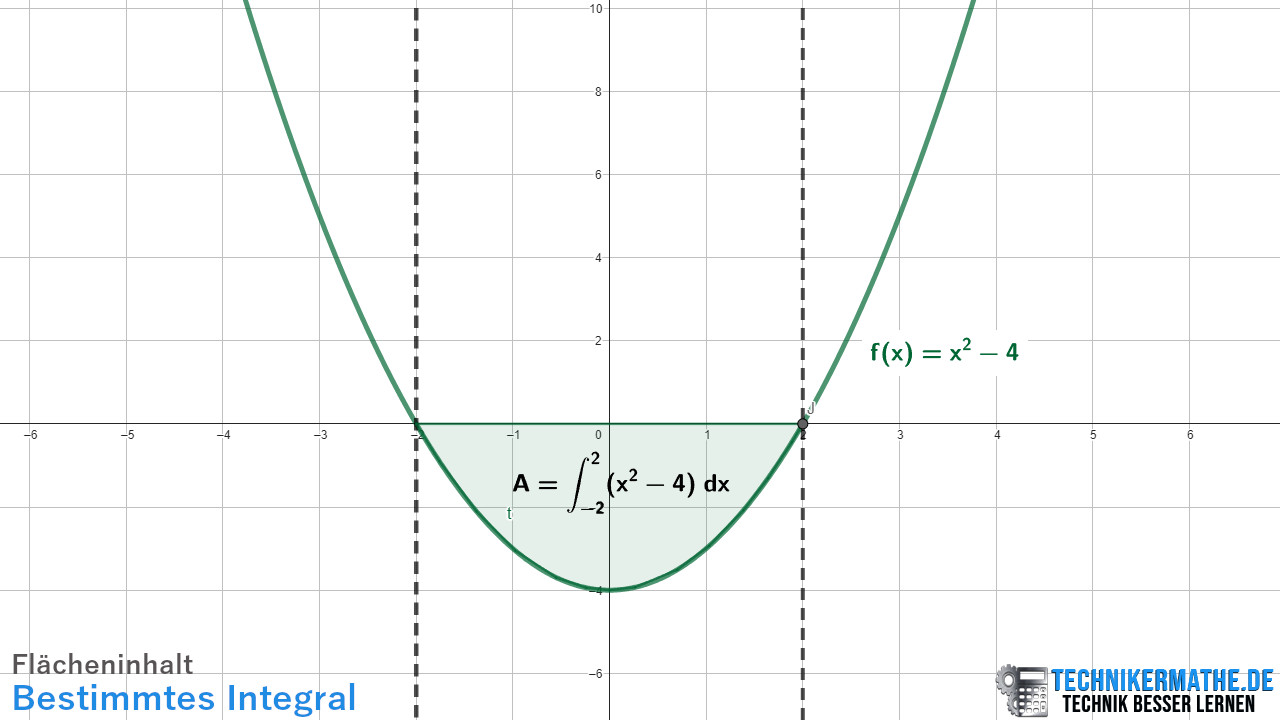
Berechne den Flächeninhalt zwischen der Parabel $f(x) = x^2 - 4$ im Intervall [-2, 2].

Nullstellen berechnen

Es ist eine quadratische Funktion gegeben und damit eine Parabel. Die Nullstellen berechnen wir, um herauszufinden, wo genau die Funktion die x-Achse schneidet. Wir können dann ermitteln, ob die gesuchte Fläche unterhalb oder oberhalb der x-Achse liegt.

Lösen von $x^2 - 4 = 0$

$x^2 = 4$

$\sqrt{x^2} = \sqrt{4}$

$x_{1,2} = \pm 2$

Die Schnittpunkte liegen bei x = -2 und x = 2. Damit liegt der Teil der Parabel zwischen diesen Werte unterhalb der x-Achse. Dies entspricht genau dem Intervall. Somit liegt die Fläche für das betrachtete Intervall unterhalb der x-Achse.

Berechnung des Integrals

Wir können den Flächeninhalt an einem Stück berechnen, da die gesamte Parabel für das betrachtete Intervall unterhalb der x-Achse liegt.

$A = \int_{-2}^{2} (x^2 - 4) \,dx$

Stammfunktion bestimmen

$F(x) = \int_{-2}^2 (x^2 - 4) \,dx = [\frac{x^3}{3} - 4x]_{-2}^2$

Grenzen einsetzen

$F(2) - F(-2) = [\frac{2^3}{3} - 4 \cdot 2] - [\frac{(-2)^3}{3} - 4 \cdot (-2)] = \frac{8}{3} - 8 = -\frac{16}{3}$

$F(2) - F(-2) = [-\frac{16}{3}] - [\frac{16}{3}] = -\frac{16}{3} - \frac{16}{3} = -\frac{32}{3}$

Die Fläche ist der Betrag des Ergebnisses:

$A = \frac{32}{3} \approx 10,67 FE$

Zusammenfassung

Bestimmte Integrale berechnen Flächen zwischen Funktion und x-Achse.
Der Unterschied zur unbestimmten Integration ist, dass das Ergebnis ein Zahlenwert ist.
Die Berechnung erfolgt durch Bildung der Stammfunktion und Einsetzen der Grenzen.
Liegt die Funktion zu integrierende unterhalb der x-Achse, muss der Betrag genommen werden, um eine Fläche zu erhalten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++