Newton Raphson Verfahren (Nullstellen) – Einfach 1a erklärt

Das Newton Raphson Verfahren, auch als Näherungsverfahren von Newton oder Newtonverfahren bezeichnet, ist eine Methode, um Lösungen (Nullstellen) von Funktionen zu finden. Es wird verwendet, wenn die Gleichung einer Funktion nicht einfach algebraisch gelöst werden kann. Das Verfahren nutzt die Idee, eine Funktion durch ihre Tangente in der Nähe einer vermuteten Lösung zu nähern.

In dieser Lerneinheit behandeln wir das Newton Raphson Verfahren.

Für ein optimales Verständnis helfen dir ein ausführliches Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der höheren Mathematik findest du im Kurs: HM1 – Höhere Mathematik 1

Was ist das Newton Raphson Verfahren?

Definition

Newton Raphson Verfahren?

Das Newton-Raphson-Verfahren ist ein iteratives Verfahren zur Bestimmung einer Nullstelle einer Funktion.

Es basiert auf der Annahme, dass eine Funktion in der Nähe einer Lösung durch ihre Tangente gut approximiert werden kann.

Der Grundgedanke des Verfahrens besteht darin, eine Tangente an die Funktion an einem Startpunkt zu legen und dann den Schnittpunkt dieser Tangente mit der x-Achse als neue Näherung für die Nullstelle zu verwenden.

Dieser Vorgang wird wiederholt, bis eine gewünschte Genauigkeit erreicht ist.

Newton Raphson Verfahren: Formel

Das Verfahren basiert darauf, dass eine Funktion $f(x)$ durch ihre Tangente an einem Punkt $x_0$ angenähert wird. Der Schnittpunkt dieser Tangente mit der x-Achse gibt die nächste Näherung $x_1$ für die Nullstelle. Dieser Prozess wird wiederholt, bis eine gewünschte Genauigkeit erreicht ist.

Die Formel für die Iteration lautet:

Newton Raphson Verfahren

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Dabei ist:

$x_n$ : die aktuelle Näherung,

$f(x_n)$ : der Funktionswert an der Stelle $x_n$ ,

$f'(x_n)$ : die Ableitung der Funktion an der Stelle $x_n$ .

Beim Newtonverfahren wird ein Startwert $x_0$ benötigt, mit welchem die Iteration gestartet wird. Der Startwert $x_0$ ist eine Anfangsschätzung, die möglichst nahe an der tatsächlichen Nullstelle der Funktion liegen sollte. Dieser Wert wird in der Regel basierend auf einer der folgenden Methoden gewählt.

Methoden für die Startwertschätzung

Grafische Analyse

Zeichne die Funktion $f(x)$ und schätze, wo die Nullstelle ungefähr liegt. Zum Beispiel:

Für $f(x) = x^2$ weiß man, dass die Nullstelle bei $\sqrt{2} \approx 1,4142$ liegt. Ein Startwert in der Nähe wie $x_0 = 1,5$ ist sinnvoll.

Vorwissen über die Funktion

Manche Funktionen haben bekannte Nullstellen oder können grob abgeschätzt werden:

Für $f(x) = x^3 - x - 1$ , bei $x \to \infty$ wächst $f(x)$ , und bei $x \to -\infty$ wird $f(x)$ negativ. Ein Test zeigt, dass bei $x = 1$ die Funktion negativ ist und bei $x = 2$ positiv. Dazwischen muss diese Funktion also die x-Achse schneiden, weil sie von den negativen in den positiven Bereich wechselt. Wir wählen also $x_0 = 1,5$ als Startwert, weil die Nullstelle zwischen 1 und 2 liegt.

Intervallmethode

Wenn man weiß, dass die Nullstelle in einem bestimmten Intervall $[a, b]$ liegt $f(a) \cdot f(b) < 0$ , kann der Mittelwert (a+b)/2 als Startwert gewählt werden.

Beispiel: Für $f(x) = x^3 - x - 1$ ist $f(1) < 0$ und $f(2) > 0$ , also liegt die Nullstelle zwischen 1 und 2. Der Startwert könnte $x_0 = 1.5$ sein.

Warum ist der Startwert wichtig?

Das Verfahren konvergiert schnell, wenn der Startwert $x_0$ nahe an der Nullstelle liegt. Ein schlechter Startwert kann dazu führen, dass das Verfahren langsam ist oder sogar divergiert (z. B. wenn die Ableitung $f'(x)$ nahe Null wird oder $f'(x)$ die falsche Richtung weist).

Betrachten wir zum Newton Raphson Verfahren das folgende Beispiel.

Beispiel 1: Polynomfunktion

Aufgabenstellung

Gegeben sei die folgende Funktion 5. Grades:

$f(x)=x^5-3x^3+x-1$

Bestimme näherungsweise eine Nullstelle dieser Funktion. Starte bei x₀ = 1,5.

Hinweis: Betrachte bei der Berechnung 4 Nachkommastellen.

Wir wollen anhand eines ausführlichen Beispiels die Vorgehensweise des Newtonverfahrens erklären. Wir zeigen dazu die betrachtete Funktion in der folgenden Grafik:

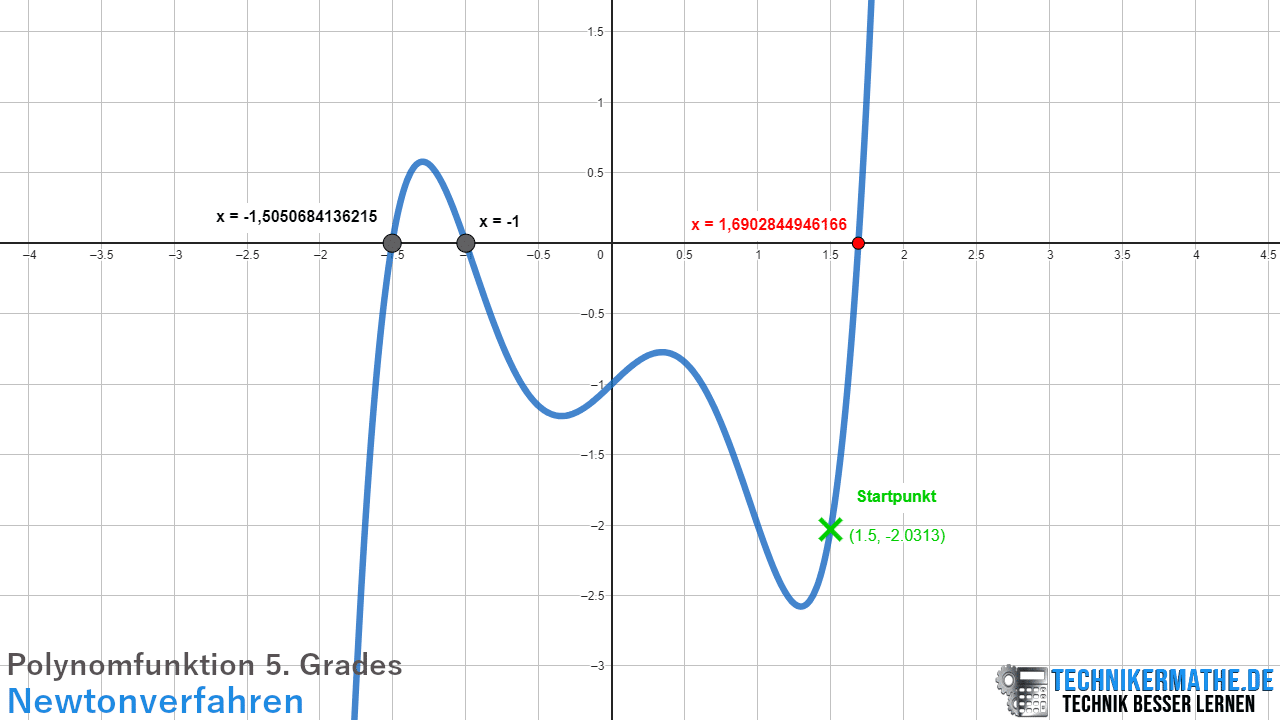
Newtonverfahren, Näherungsverfahren nach Newton, Newton Raphson Verfahren, Polynomfunktion — Newton Raphson Verfahren – Beispiel

In der oben gezeigten Grafik ist die Funktion 5. Grades dargestellt, die insgesamt drei Nullstellen aufweist. Mit dem Newton-Verfahren und einem geeigneten Startwert lässt sich eine dieser Nullstellen berechnen. Dabei ist es entscheidend, die ungefähre Position der Nullstelle zu kennen, damit der Startwert möglichst nah an der gesuchten Nullstelle liegt. Wir beginnen mit einem Startwert von x = 1,5 und nähern uns so der Nullstelle bei x = 1,6903. Wie dieser Prozess genau funktioniert, erklären wir dir Schritt für Schritt.

Für die ersten beiden Iterationen veranschaulichen wir das Vorgehen zusätzlich mit einer grafischen Darstellung, damit du den Ablauf besser nachvollziehen kannst.

Merk’s dir!

Andere Nullstellen

Du kannst auch die anderen Nullstellen mittels Newtonverfahren bestimmen. Hierzu könntest du die Startwerte ändern. So kannst du die Nullstelle bei x = -1,5051 z.B. mit dem Startwert x = -1,5 annähern.

Wir wollen nun mit dem Startwert von x₀ = 1,5 zeigen, wie das Näherungsverfahren von Newton funktioniert.

1. Iteration (n = 0)

Startwert: $x_0 = 1,5$

Funktion: $f(x)=x^5-3x^3+x-1$

Funktionswert: $f(1,5) = -2,0313$

Ableitung: $f'(x) = 5x^4 - 9x^2 +1$

Ableitungswert: $f(1,5) = 6,0625$

Wir wenden das Newton Raphson Verfahren an:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Mit n = 0 ergibt sich:

$x_{0+1} = x_0 - \frac{f(x_0)}{f'(x_0)}$

Einsetzen der Werte:

$x_1 = 1,5 - \frac{-2,0313}{6,0625} = 1,8351$

In der folgenden Grafik siehst du die 1. Iteration:

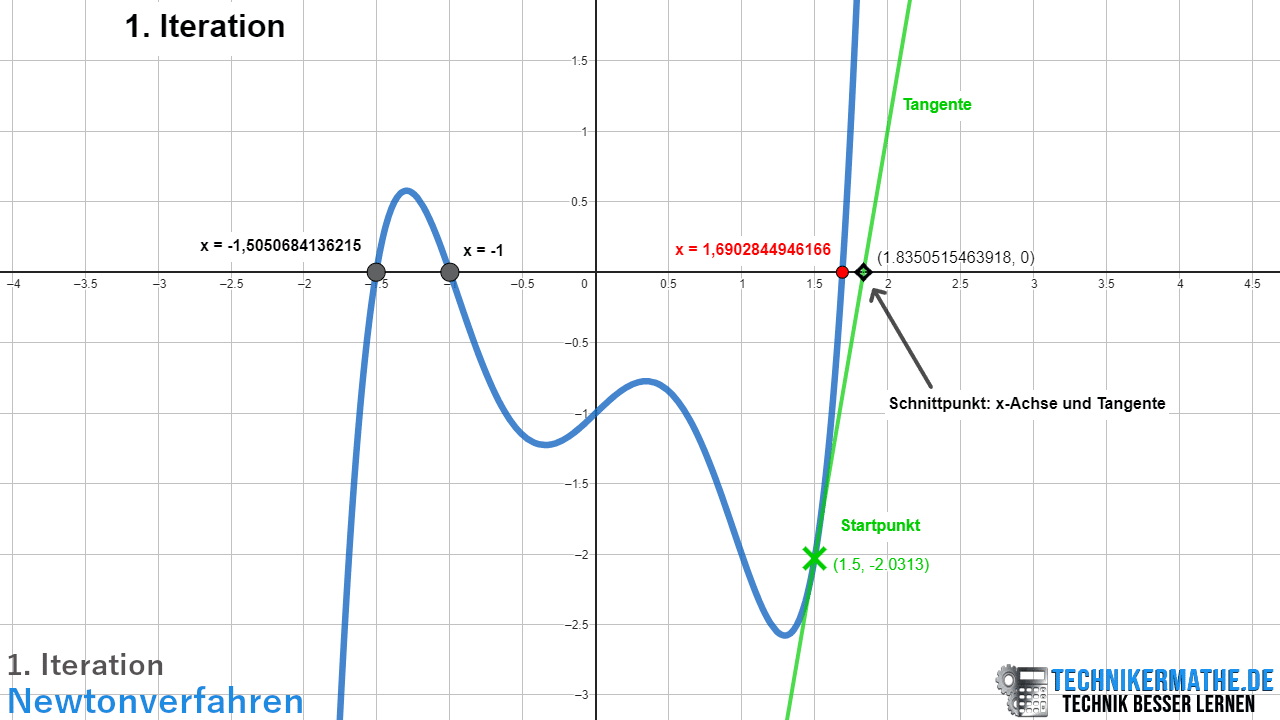
Newtonverfahren, Näherungsverfahren nach Newton, Newton Raphson Verfahren, Nullstelle, Iteration, Näherungsverfahren, Beispiel — 1. Iteration – Newton Raphson Verfahren

In der obigen Grafik siehst du die 1. Iteration. Gestartet wird bei einem Wert von x₀ = 1,5. Der dazugehörige Funktionswert lautet f(x) = -2,0313. Wir berechnen die Tangente (siehe Lerneinheit Tangentengleichung dieses Kapitels) für den betrachteten Startpunkt. Dort wo die Tangente die x-Achse schneidet, liegt der Startwert für die 2. Iteration. Die Tangente schneidet die x-Achse bei x = 1,8351 (4 Nachkommastellen).

2. Iteration (n = 1)

Startwert: $x_1 = 1,8351$

Funktion: $f(x)=x^5-3x^3+x-1$

Funktionswert: $f(1,8351) = 3,1068$

Ableitung: $f'(x) = 5x^4 - 9x^2 +1$

Ableitungswert: $f(1,8351) = 27,3951$

Wir wenden das Newtonverfahren an:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Mit n = 1 ergibt sich:

$x_2 = x_1 - \frac{f(x_1)}{f'(x_1)}$

Einsetzen der Werte:

$x_2 = 1,8351 - \frac{3,1068}{27,3951} = 1,7217$

Wir bilden die Differenz:

$|\Delta x| = |x_2 - x_1| = |1,7217 - 1,8351| = 0,1134$

In der folgenden Grafik siehst du die 1. Iteration:

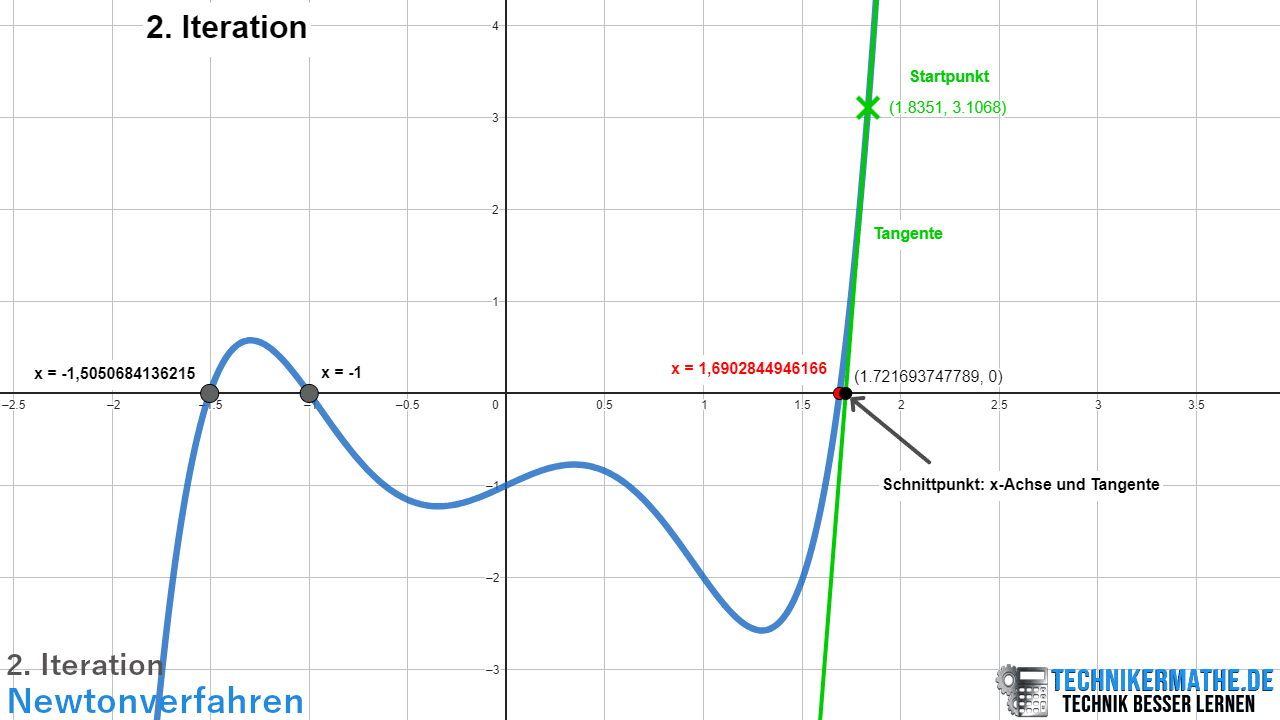
2. Iteration, Newtonverfahren, Beispiel, Newton Raphson, Nullstellen, Näherungsfunktion — 2. Iteration: Newton Raphson Verfahren

In der obigen Grafik siehst du die 2.Iteration. Gestartet wird bei einem Wert von x₁ = 1,8351. Der dazugehörige Funktionswert lautet f(x) = 3,1068. Wir berechnen die Tangente (siehe Lerneinheit Tangentengleichung dieses Kapitels) für den betrachteten Startpunkt. Dort wo die Tangente die x-Achse schneidet, liegt der Startwert für die 3. Iteration. Die Tangente schneidet die x-Achse bei x = 1,7217 (4 Nachkommastellen).

3. Iteration (n = 2)

Startwert: $x_2 = 1,7217$

Funktion: $f(x)=x^5-3x^3+x-1$

Funktionswert: $f(1,7217) = 0,5393$

Ableitung: $f'(x) = 5x^4 - 9x^2 +1$

Ableitungswert: $f(1,7217) = 18,2557$

Wir wenden das Newtonverfahren an:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Mit n = 2 ergibt sich:

$x_3 = x_2 - \frac{f(x_2)}{f'(x_2)}$

Einsetzen der Werte:

$x_3 = 1,7217 - \frac{0,5393}{18,2557} = 1,6922$

Wir bilden die Differenz:

$|\Delta x| = |x_3 - x_2| = |1,6922 - 1,7217 | = 0,0295$

Die Differenz zwischen den x-Werten wird immer kleiner. Wir können den Wert noch weiter annähern.

4. Iteration (n = 3)

Startwert: $x_3 = 1,6922$

Funktion: $f(x)=x^5-3x^3+x-1$

Funktionswert: $f(1,6922) = 0,031$

Ableitung: $f'(x) = 5x^4 - 9x^2 +1$

Ableitungswert: $f(1,6922) = 16,2275$

Wir wenden das Newtonverfahren an:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Mit n = 3 ergibt sich:

$x_4 = x_3 - \frac{f(x_3)}{f'(x_3)}$

Einsetzen der Werte:

$x_4 = 1,6922 - \frac{0,031}{16,2275} = 1,6903$

Wir bilden die Differenz:

$|\Delta x| = |x_4 - x_3| = |1,6903 - 1,6922 | = 0,0019$

Die Differenz zwischen den x-Werten wird immer kleiner. Wir können den Wert noch weiter annähern.

5. Iteration (n = 4)

Startwert: $x_4 = 1,6903$

Funktion: $f(x)=x^5-3x^3+x-1$

Funktionswert: $f(1,6903) = 0,00025$

Ableitung: $f'(x) = 5x^4 - 9x^2 +1$

Ableitungswert: $f(1,6903) = 16,1015$

Wir wenden das Newtonverfahren an:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Mit n = 4 ergibt sich:

$x_5 = x_4 - \frac{f(x_4)}{f'(x_4)}$

Einsetzen der Werte:

$x_5 = 1,6903 - \frac{0,00025}{16,1015} = 1,6903$

Wir bilden die Differenz:

$|\Delta x| = |x_5 - x_4| = |1,6903 - 1,6903| = 0$

Wir haben bei Betrachtung von 4 Nachkommastellen eine Differenz von 0 gegeben. Damit ändert sich der x-Wert nicht mehr und wir haben die Nullstelle der Funktion näherungsweise bei x₁ = 1,6903 berechnet.

Bisher haben wir nur eine Nullstelle des Polynoms näherungsweise berechnet. Beim Newton-Verfahren hängt die gefundene Nullstelle stark vom gewählten Startwert ab. Für andere Startwerte könnten wir auf andere Nullstellen stoßen, da $f(x) = x^5 - 3x^3 + x - 1$ ein Polynom fünften Grades ist und daher bis zu fünf Nullstellen haben kann (reelle oder komplexe).

Häufige Fehlerquellen und Herausforderungen

Wahl des Startwerts: Der Startwert $x_0$ ist entscheidend für die Konvergenz des Verfahrens. Wenn der Startwert zu weit von der tatsächlichen Nullstelle entfernt ist oder wenn die Ableitung an diesem Punkt null ist, kann das Verfahren versagen oder sehr langsam konvergieren.
Divergenz: Wenn die Ableitung 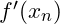$f'(x_n)$ an einer Stelle null wird oder sehr klein ist, kann das Verfahren instabil werden. In solchen Fällen kann die Methode nicht konvergieren und divergenzieren.
Mehrere Nullstellen: Das Verfahren findet nur die Nullstelle, die dem gewählten Startwert am nächsten liegt. Wenn eine Funktion mehrere Nullstellen hat, kann das Verfahren je nach Wahl des Startwerts zu unterschiedlichen Lösungen führen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

Was passiert, wenn der Startwert zu weit von der Nullstelle entfernt ist?

Wenn der Startwert zu weit entfernt ist, kann das Verfahren entweder sehr langsam konvergieren oder sogar divergieren, d. h. es wird keine Nullstelle gefunden. Eine genauere Schätzung des Startwerts ist daher wichtig.

Wie schnell konvergiert das Newton-Raphson-Verfahren?

Das Verfahren konvergiert in der Regel sehr schnell, insbesondere wenn der Startwert nahe an der Nullstelle liegt. In vielen Fällen erreicht das Verfahren eine hohe Genauigkeit in nur wenigen Iterationen.

Kann das Verfahren bei Funktionen mit mehreren Nullstellen verwendet werden?

Ja, das Verfahren kann verwendet werden, um eine von mehreren Nullstellen zu finden. Der Startwert bestimmt, welche Nullstelle gefunden wird. Für jede Nullstelle kann ein anderer Startwert gewählt werden.

Warum ist die Ableitung im Newton-Verfahren wichtig?

Die Ableitung $f'(x_n)$ wird verwendet, um die Steigung der Tangente an die Funktion zu bestimmen. Diese Tangente gibt den nächsten Näherungswert für die Nullstelle an.

Was passiert, wenn die Ableitung null wird?

Wenn $f'(x_n) = 0$ , kann das Verfahren nicht fortgesetzt werden, da die Division durch null zu einer undefinierten Berechnung führt. In diesem Fall muss der Startwert angepasst werden.

Zusammenfassung

Das Newton-Raphson-Verfahren ist ein leistungsstarkes und schnelles Verfahren zur Bestimmung der Nullstellen einer Funktion. Es verwendet die Tangente an die Funktion, um den nächsten Näherungswert zu berechnen und iteriert diesen Prozess, bis die gewünschte Genauigkeit erreicht ist. Die Wahl des Startwerts ist entscheidend für den Erfolg des Verfahrens, da ein ungünstiger Startwert zu langsamer Konvergenz oder sogar zur Divergenz führen kann. Das Verfahren findet in vielen praktischen Anwendungen, wie der numerischen Mathematik und der Ingenieurwissenschaft, breite Anwendung. Es ist besonders nützlich, wenn algebraische Lösungen schwer zu finden sind oder nicht existieren.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++