PH1 – Rechtwinklige Dreiecke

Ein rechtwinkliges Dreieck zeichnet sich dadurch aus, dass einer von drei Winkeln ein 90°-Winkel darstellt. Ein 90°-Winkel wird auch als rechter Winkel bezeichnet und mit einem Punkt im Winkel angegeben.

Für ein optimales Verständnis hilft dir ein ausführlicher Videoclip zum Thema. Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH1 – Grundlagen der Physik.

In dieser Lerneinheit schauen wir uns rechtwinklige Dreiecke an und zeigen dir, wie du die Seiten richtig beschriftest!

Für die Berechnungen von Winkeln und Seitenlängen innerhalb der technischen Mechanik ist die Kenntnis über die Trigonometrie am rechtwinkligen Dreieck notwendig.

Rechtwinklige Dreiecke

Wir betrachten zunächst ein rechtwinkliges Dreieck und zeigen dir, wie die Seiten bezeichnet werden:

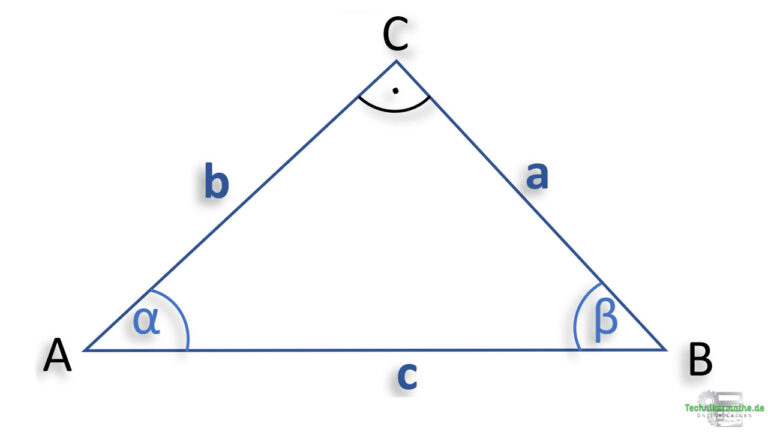
In der obigen Grafik ist ein rechtwinkliges Dreieck mit den drei Seite a, b und c und den spitzen Winkeln $\alpha$ und $\beta$ zu sehen. Der rechte Winkel ist ein 90°-Winkel und wird mit einem Punkt im Winkel dargestellt.

rechtwinklige dreiecke, hypotenuse — rechtwinklige Dreiecke

Die Seite, die dem rechten Winkel gegenüberliegt, wird als Hypotenuse bezeichnet. Die beiden Seiten, die den rechten Winkel einschließen (hier: a und b), werden als Kathetenseiten bezeichnet. Je nachdem welcher Winkel betrachtet wird, ist eine Kathetenseite die Ankathete und eine die Gegenkathete.

Rechtwinklige Dreiecke: Seiten in Bezug auf Winkel α

Beschriftung der Seiten in einem rechtwinkligen Dreieck ausgehend vom Winkel Alpha — Beschriftung der Seiten ausgehend vom Winkel Alpha

Betrachten wir den Winkel α im obigen rechtwinkligen Dreieck, so ist die Kathetenseite die an diesem Winkel liegt die ANkathete und die Seite die gegenüber von dem betrachteten Winkel liegt die GEGENkathete. Die gegenüberliegende Seite vom Winkel $\alpha$ ist die Gegenkathete [Seite a] zu diesem Winkel, die Seite am Winkel $\alpha$ ist die Ankathete [Seite b].

Rechtwinklige Dreiecke: Seiten in Bezug auf Winkel β

Beschriftung der Seiten in einem rechtwinkliges Dreieck ausgehend vom Winkel Beta — Beschriftung der Seiten ausgehend vom Winkel Beta

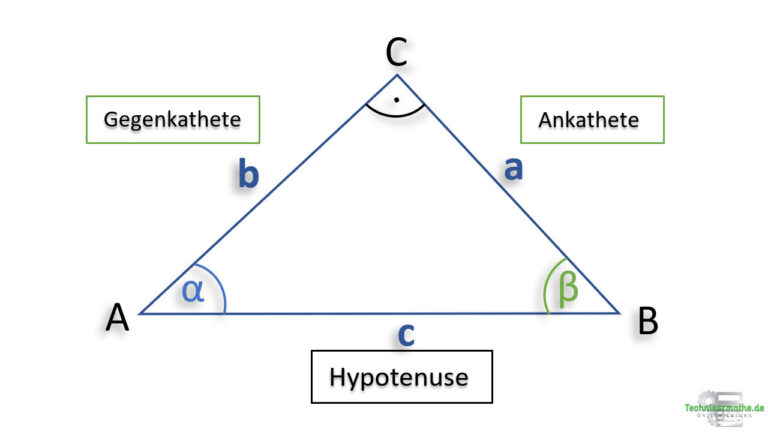
Betrachten wir hingegen den Winkel β, so ändern sich die beiden Kathetenseiten. Die gegenüberliegende Seite vom Winkel $\beta$ ist die Gegenkathete [Seite b] zu diesem Winkel, die Seite am Winkel $\beta$ ist die Ankathete [Seite a].

Merk’s dir!

Für die Trigonometrie am rechtwinkligen Dreieck ist es wichtig die drei Seiten benennen zu können. Die Hypotenuse liegt immer gegenüber vom rechten Winkel. Die Ankathete liegt immer am betrachteten Winkel und die Gegenkathete immer gegenüber vom betrachteten Winkel.

Innerhalb der Technischen Mechanik ist die Anwendung der Trigonometrie am rechtwinkligen Dreieck unverzichtbar. Viele geometrische Körper bzw. Flächen können so aufgeteilt werden, dass ein rechtwinkliges Dreieck entsteht. Mittels der Trigonometrie kannst du dann Seitenlängen und Winkel ermitteln, die für die weiteren Berechnungen notwendig sind.

Allgemeine Dreiecke mit Höhe h

Das allgemeine Dreieck zeichnet sich dadurch aus, dass es keinen rechten Winkel aufweist. Alle drei gegebenen Winkel sind demnach ungleich 90°. Wir können die Trigonometrie am rechtwinkligen Dreieck hier also zunächst nicht anwenden. Es ist aber möglich das allgemeine Dreieck in zwei rechtwinklige Dreiecke aufzuteilen, indem wir eine Höhe $h$ einzeichnen.

Du hast nun zwei rechtwinklige Dreiecke gegeben und kannst auf jedes von diesen Teildreiecken die Trigonometrie am rechtwinkligen Dreieck (folgende Lerneinheit) anwenden.

Du solltest in jedem Fall beachten, dass der Winkel γ durch die Höhe h geteilt wird und jedes Teildreieck einen Anteil des Winkels erhält. Das linke Teildreieck weist damit den Winkel γ₁ und das rechte Teildreieck den Winkel γ₂ auf. Die beiden Winkel sind dann identisch, wenn du ein gleichseitiges oder gleichschenkliges Dreieck gegeben hast.

Für jedes Dreieck gilt, dass die Summe seiner Winkel 180° ergeben muss, demnach muss auch die Summe der Winkel im jeweiligen Teildreieck 180° ergeben.

Für das linke Teildreieck gilt also:

$\alpha + 90^{\circ} + \gamma_1 = 180^{\circ}$

Für das rechte Teildreieck gilt:

$\beta + 90^{\circ} + \gamma_2 = 180^{\circ}$

Gleichschenklige und gleichseitige Dreiecke

In der nachfolgenden Grafik zeigen wir dir den Unterschied zwischen einem gleichschenkligen und einem gleichseitigen Dreieck auf:

In einem gleichschenkligen Dreieck sind die beiden Schenkel, also die Seite a und b gleich lang (a = b). Damit sind auch die beiden unteren Winkel α und β gleich groß (α = β). Der Winkel γ hingegen ist ungleich der beiden Winkel α und β. Wenn du nun aber die Höhe h einzeichnest, dann teilt sich der Winkel γ genau in zwei gleich große Teile. Damit sind für das linke und das rechte Teildreieck die beiden Winkel γ₁ und γ₂ gleich groß.

In einem gleichseitigen Dreieck sind alle drei Seite gleich lang (a = b = c). Damit sind auch alle gegebenen Winkel gleich groß (α = β = γ). Auch hier gilt, dass der Winkel γ sich genau in zwei gleich große Winkel teilt, wenn die Höhe h eingezeichnet wird.

Video: Rechtwinklige Dreiecke

In dem nachfolgenden Video zeige ich dir, wie du allgemeine Dreiecke in zwei rechtwinklige Dreiecke aufteilst:

Aus dem Video weißt du nun also, dass eine Höhe $h$ aus einem allgemeinen Dreieck zwei rechtwinklige Dreiecke macht und dass die Winkelsumme eines Dreiecks 180° betragen muss. Mit diesem Wissen kannst du nun die Trigonometrie am rechtwinkligen Dreieck anwenden.

Tausende interaktive Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++