(ET5-22) Komplexe Wechselstromschaltungen – Die symbolische Methode

In diesem Kurstext erklären wir dir einfach und ausführlich, was die Symbolische Methode in der Wechselstromtechnik ist und wie man mit dieser arbeitet.

Symbolische Methode – Überblick

undefiniert

Aaah, ich erinnere mich....

Wie du in den vorangegangenen Kurstexten bereits erfahren hast, kann man mit komplexen Spannungen und komplexen Strömen, welche die Eigenschaft von $j \omega$ als Differentialoperator besitzen, sowie genau definierten Impedanzen und Admittanzen die Differentialgleichungen eines Netzwerks in algebraische Gleichungen überführen. Dadurch fällt die Berechnung wesentlich leichter aus.

“Die Verwendung der symbolischen Methode in der komplexen Wechselstromtechnik macht die Berechnung noch mal leichter. Denn hier verzichtet die symbolische Methode darauf zuvor eine Differentialgleichung aufzustellen und transformiert das Schaltbild direkt ins Komplexe.”

Grundsätzlich ist die symbolische Methode der Wechselstromtechnik eine Verallgemeinerung der komplexen Wechselstromrechnung. Sie bezieht sich auf exponentiell anschwellende sowie abklingende Sinussignale.

“Nicht selten spricht man im Zusammenhang mit der symbolischen Methode von einer Transformation sinusförmiger Signale des Zeitbereiche in die komplexen Amplituden des Frequenzbereichs.”

Zweck der Symbolischen Methode

Die Symbolische Methode hilft komplexe Berechnungen von Wechselstromnetzwerken auf Methoden von Gleichstromnetzwerken zu überführen, jedoch bedeutet diese nicht, dass es sie auf die Einfachheit dieser reduziert.

Symbolische Methode – Lösungsprogramm

“Das Lösungsprogramm erfolgt in 5 aufeinander folgenden Schritten.“

Schritt 1: Ersatz der Spannungen und Ströme (Symbolische Methode)

Zuerst ersetzen wir alle im Schaltbild befindlichen stationären Sinusspannungen und Sinusströme durch ihre zeitunabhängigen komplexen Amplituden oder Effektivwerte.

Schritt 2: Ersatz der linearen Zweipolgleichungen (Symbolische Methode)

Danach ersetzen wir alle im Schaltbild befindlichen linearen Zweipolgleichungen der elektrischen Bauteile durch ihre Impedanzen oder Admittanzen. Dies gelingt durch den Ersatz des Differentialoperators $j \cdot \omega$ .

Schritt 3: Algebraisches Gleichungssystem aufstellen (Symbolische Methode)

Jetzt stellen wir das algebraische Gleichungssystem des Netzwerks auf. Hierzu bedienen wir uns ganz einfach der bereits bekannten Rechenregeln aus der Gleichstromtechnik.

Dabei sind zu nennen:

Ohmsches Gesetz,

Maschensatz nach Kirchhoff,

Knotensatz nach Kirchhoff,

Regel für Reihenschaltungen,

Regel für Parallelschaltungen,

Stromteilerregel,

Spannungsteilerregel.

Hinzu kommen die vereinfachten Analyseverfahren für lineare Netzwerke.

Schritt 4: Auflösen der algebraischen Gleichungssysteme (Symbolische Methode)

Mit den bekannten mathematischen Methoden für lineare Gleichungssystem lösen wir das algebraische Gleichungssystem auf. Damit können wir die komplexen Amplituden oder Effektivwerte der unbekannten Größen ermitteln. Die ermittelten Werte haben dann ausreichend Aussagekraft und können als Zeigerdiagramm oder als Ortskurven verbildlicht werden.

“Wählt man die Darstellung in Form der Exponentialschreibweise, so können die reellen Amplituden und Nullphasen direkt abgelesen werden. Damit endet dann die Berechnung.”

Schritt 5: Rücktransformation (optional) (Symbolische Methode)

Falls es in der Aufgabenstellung gefordert wird, kann man mit Hilfe der Rücktransformation die Ergebnisse von den komplexen Amplituden oder Effektivwerten in reellen Signalen angeben. Dies erfolgt durch die Multiplikation mit $e^{j \cdot \omega \cdot t}$ oder $\sqrt{2} \cdot e^{j \cdot \omega \cdot t}$ und der anschließenden Bildung des Realteils und Imaginärteils.

Symbolische Methode – Fourier-Transformation

Wie du bereits oben gelesen hast, sprechen wir von einer Transformation der sinusförmigen Signale des Zeitbereichs in die komplexen Methoden des Frequenzbereichs. Eine anschauliche Variante um dies darzustellen ist die Fourier-Transformation.

Exemplarisch führen wir die für eine Spannung im Zeitbereich durch und führen als neue Größe den Fourierkoeffizienten $\underline{c}_n$ ein:

$\boxed{\underline{c}_n = \frac{2}{T} \int_T \hat{u} \cdot cos (\omega \cdot t + \varphi_u) \cdot e^{-j \cdot n \cdot \omega \cdot t} dt }$

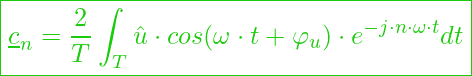
daraus ergibt sich:

$\boxed{\underline{c}_n = \frac{\hat{u}}{T} \int_T \cdot (e^{j\cdot (\omega \cdot t + \varphi_u)} + e^{- j\cdot (\omega \cdot t + \varphi_u)} \cdot e^{- j \cdot n \cdot \omega \cdot t} dt }$

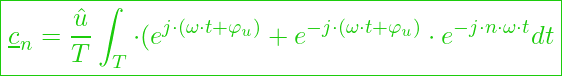
dies entspricht letztlich:

$\boxed{\underline{c}_{n=1} = \underline{\hat{U}} }$

oder

$\boxed{ \underline{c}_{n=1} = \underline{U} \cdot \sqrt{2} }$

Wir haben jetzt die komplexe Amplitude bzw. den komplexen Effektivwert im Frequenzbereich gegeben. Es zeigt sich, dass die Fourierkoeffizienten $\underline{c}_n$ genau den ruhenden komplexen Zeigern $\underline{U}$ bzw. $\underline{\hat{U}}$ darstellen.

“Die Fourier-Transformation ist somit eine Rechenoperation, womit man zeitabhängige reelle Ströme und Spannungen in eine komplexe Beschreibung zu überführen kann und sie anschließend zurücktransformiert.”

Beispiel: Tiefpass (Symbolische Methode)

undefiniert

Beispiel: Tiefpass

Damit du eine praktische Vorstellung von dem Lösungsprogramm für die symbolische Methode erhältst, wollen wir eine beispielhafte Berechnung durchführen. Hierzu wählen wir einen Tiefpass.

Erklärung – Tiefpass

Falls du nicht wissen solltest was ein Tiefpass ist, hier die kurze Erklärung:

“Ein Tiefpass ist ein in der Elektrotechnik verwendeter Filter, welche Anteile von Signalen mit Frequenz unterhalb einer festgelegten Grenzfrequenz annähernd ungehindert durchlassen, jedoch Anteile von Signalen, die oberhalb der Grenzfrequenz liegen, derart dämpfen, dass sie den Grenzwert nicht mehr überschreiten. Du findest solche Filter in der Mechanik, Hydraulik oder Akustik. Die Abschwächung bewirkt zudem eine Zeitverzögerung, die eine Verschiebung des Phasenwinkels eines Sinussignalverlaufs verursacht.”

In Netzwerken bzw. Schaltplänen erkennst du Tiefpassfilter an dem nachfolgenden Schaltzeichen:

Symbolische Methode - Beispiel - Tiefpass — Symbolische Methode – Beispiel – Tiefpass

undefiniert

Was hat der Tiefpass mit den bisher bekannten Schaltelementen zu tun?....

Falls du dir jetzt diese Frage stellt, dann können wir dir direkt sagen: Sehr viel sogar. Denn der Tiefpass ist in den meisten Fällen ein passiver analoger Tiefpass, welcher aus Widerständen, Spulen und Kondensatoren besteht. Daher eignet sich der Tiefpass besonders gut für unser Beispiel.

Wenn es einen passiven analogen Tiefpass gibt, dann sollte es ja auch einen aktiven analogen Tiefpass geben, oder? Richtig!

Ein aktiver analoger Tiefpass besitzt zudem noch Operationsverstärker oder Transistoren.

Aufgabenstellung

Da jetzt weißt, was ein Tiefpass ist können wir mit der Aufgabe starten.

Uns ist folgendes Schaltbild eines Tiefpasses im Bildbereich der komplexen Wechselstromrechnung gegeben:

Symbolische Methode - Tiefpassfilter — Symbolische Methode – Tiefpassfilter

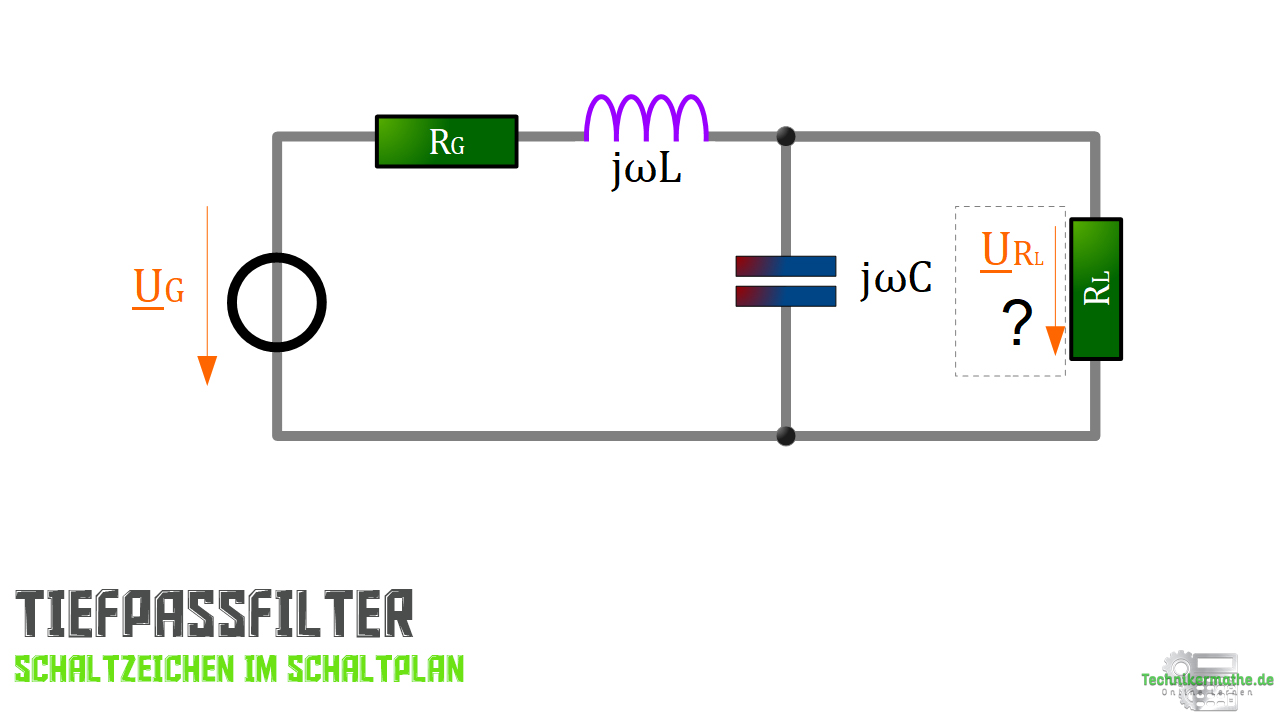
In diesem Schaltbild finden wir eine Spannungsquelle (Generator), zwei Widerstände (Generatorwiderstand $R_G$ und Lastwiderstand $R_L$ ), eine Induktivität (Spule) und eine Kapazität (Kondensator).

Als Angabe für die Berechnung liegen uns die Generatorspannung $\underline{U_G}$ und alle anderen Werte der elektrischen Bauteile vor.

Die gesuchte Größe ist die Spannung $\underline{U}_{R_L}$ am Lastwiderstand. Beide haben die komplexen Effektivwerte als Beschriftung.

Die elektrischen Bauteile sind alle durch ihre komplexen Impedanzen gekennzeichnet.

Lösung

Wir können jetzt unter Hinzunahme der Regeln für die Reihen- und Parallelschaltung, sowie der Spannungsteilerregel die notwendige Gleichung aufstellen:

$\boxed{ \underline{U}_{R_L} = \underline{U}_G \cdot \frac{ R_L || \frac{1}{j \cdot \omega \cdot C}}{R_G + (j \cdot \omega \cdot L) + R_L || \frac{1}{j \cdot \omega \cdot C}} }$

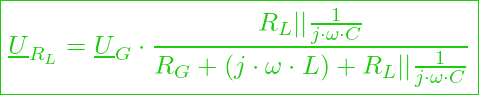
Im ersten Schritt dividieren wir den Zähler und den Nenner durch $R_L || \frac{1}{j \cdot \omega \cdot C}$ und erhalten

$\boxed{\underline{U}_{R_L} = \underline{U}_G \cdot \frac{1}{\frac{R_G + (j \cdot \omega \cdot L}{R_L || \frac{1}{j \cdot \omega \cdot C}} + 1} }$

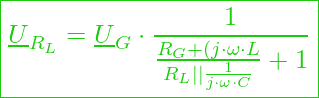
Im nächsten Schritt lösen wir den Doppelbruch auf mit $\frac{1}{R_L || \frac{1}{j \cdot \omega \cdot C}} = \frac{1}{R_L} + j \cdot \omega \cdot C$ und erhalten

$\boxed{ \underline{U}_{R_L} = \underline{U}_G \cdot \frac{1}{(R_G + j \cdot \omega \cdot L) \cdot (\frac{1}{R_L} + j \cdot \omega \cdot C) + 1} }$

Das gesuchte Übertragungsverhalten im Frequenzbereich können wir jetzt mit einem nach Realteil und Imaginärteil geordneten Nenner darstellen:

$\boxed{\underline{U}_{R_L} = \frac{\underline{U}_G}{1 + \frac{R_G}{R_L} - \omega^2 \cdot L \cdot C + j \cdot \omega \cdot (\frac{L}{R_L} + R_G \cdot C)} }$

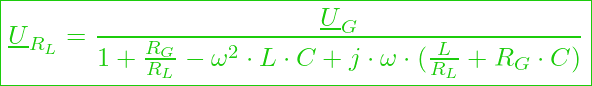
Über diesen Rechenschritt hinaus, könnten wir jetzt noch eine Normierung vornehmen und das Ergebnis als Ortkurve darstellen. Man kann jetzt noch eine Exponentialschreibweise wählen, um den Frequenzgang von der Amplitude und der Phase separat abzulesen und anschließend grafisch darzustellen:

$\boxed{\frac{\underline{U}_{R_L}}{\underline{U}_G} = \frac{1}{\sqrt{(1 + \frac{R_G}{R_L} - \omega^2 \cdot L \cdot C)^2 + \omega^2 \cdot (\frac{L}{R_L} + R_G \cdot C)^2} \cdot exp( - j \cdot arctan \frac{\omega \cdot (\frac{L}{R_L} + R_G \cdot C)}{1 + \frac{R_G}{R_L} - \omega^2 \cdot L \cdot C}) }}$

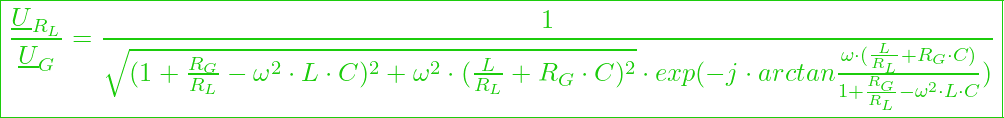
An dieser Stelle möchten wir noch mal betonen, dass eine solche Aufgabe vermutlich nicht in deiner Prüfung drankommt, jedoch solltest du diese einfach mal gesehen haben, um sie zu verstehen. Hätten wir jetzt ganz normal mit Differentialgleichungen gerechnet, so kämen wir zwar auf das gleiche Ergebnis mit dem entscheidenden Unterschied, dass der Berechnungsaufwand um ein vielfaches höher gewesen wäre.

Symbolische Methode – Zeigerdarstellung

Für die grafische Darstellung von komplexen Größen verwenden wir ja bekanntlich die Zeigerdarstellung. Auf dem Weg dahin gelten immer die Regeln für die Parallelschaltung, die Reihenschaltung, sowie der Maschensatz und der Knotensatz nach Kirchhoff.

Reihenschaltung

Im Zeigerbild legen wir die Bezugsgröße in die reelle Achse. Bei einer Reihenschaltung der elektrischen Bauteile, wählen wir den Strom als zweckmäßige Größe und liegen den Zeiger in die reelle Achse.

Für jedes Bauteil, welches durch den selben Strom durchflossen wird, können wir die angelegten Spannungen ermitteln, als Zeiger darstellen und mittels Vektoraddition zusammenfassen.

Alternativ lassen sich alle komplexen Widerstände addieren und anschließend mit dem Strom multiplizieren.

Parallelschaltung

Bei einer Parallelschaltung der elektrischen Bauteile, geben wir als zweckmäßige Größe die Spannung vor und können anschließend für jedes Bauteil den Strom getrennt berechnen und anschließend alle komplexen Ströme durch Vektoraddition der Zeiger verbinden.

Alternativ lassen sich alle komplexen Leitwerte addieren und anschließend mit der Spannung multiplizieren.

Mischschaltung

Liegt eine Mischschaltung, als eine Kombination von Reihen- und Parallelschaltung vor, so empfiehlt es sich diese passend zu zerlegen, die Teilelementen einzeln zu berechnen und sie anschließend wieder zusammenzuführen.

Beispiel: Zeigerdarstellung – Reihenschaltung (Symbolische Methode)

undefiniert

Beispiel: Reihenschaltung von RC

Abschließend zu diesem Thema schauen wir uns noch mal eine Aufgabe an.

Aufgabenstellung

Wir haben eine Reihenschaltung von einem Widerstand $R$ und einem Kondensator $C$ gegeben. Zudem liegt eine Wechselspannung vor.

Die Kennwerte sind:

$\boxed{ R = 150 \Omega }$ – Wirkwiderstand

$\boxed{ C = 10 \mu F }$ – Kapazität

$\boxed{ \omega = 500 s^{-1} }$ – Wechselspannung

Ermittle den Blindwiderstand $X_C$ , die Gesamtimpedanz $\underline{Z}$ , den Scheinwiderstand $Z$ sowie den Phasenverschiebungswinkel $\varphi$

Lösung

Blindwiderstand

Im ersten Schritt können wir jetzt den Blindwiderstand mit den gegebenen Größen ermitteln

$\boxed{ X_C = - \frac{1}{\omega \cdot C} = - \frac{1}{500 s^{-1} \cdot 10^{-5} F} = - 200 \Omega }$

Gesamtimpedanz

Um jetzt die Gesamtimpedanz (Summe aus Wirkwiderstand und Blindwiderstand) als komplexe Größe ermitteln zu können, schauen wir uns zuerst die richtige Umrechnung für die Maßeinheiten an:

$\boxed{ F = \frac{A\cdot s}{V} = \frac{s}{\Omega} }$

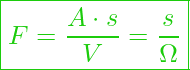
jetzt stellen wir die typische Gleichung für eine Reihenschaltung auf:

$\boxed{ \underline{Z} = \underline{Z}_R + \underline{Z}_C }$

Dies entspricht:

$\boxed{\underline{Z} = R + j \cdot X_C }$

mit Zahlenwerten:

$\boxed{\underline{Z} = 150 \Omega - j \cdot 200 \Omega }$

Scheinwiderstand

Der Scheinwiderstand als Betrag der Impedanz, ist das Verhältnis der Beträge von Spannung sowie Strom und ergibt sich durch die Verwendung des Satz des Pythagoras:

$\boxed{ Z = |\underline{Z}| = \sqrt{(Re{\underline{Z}})^2 + (Im{\underline{Z}})^2} }$

mit Zahlenwerten:

$\boxed{ Z = \sqrt{(150 \Omega)^2 + (200 \Omega)^2} }$

Phasenverschiebungswinkel

Den Phasenverschiebungswinkel zwischen der Spannung und dem Strom ermitteln wir wie folgt:

$\boxed{\varphi = arctan \frac{Im{\underline{Z}}}{Re{\underline{Z}}} }$

mit Zahlenwerten:

$\boxed{\varphi = arctan \frac{-200 \Omega}{150 \Omega} = -53,13 ^{\circ} }$

Mit der Angabe des Phasenverschiebungswinkels können wir die Gesamtimpedanz alternativ als Schreibweise in Polarkoordinaten angeben:

$\boxed{\underline{Z} = 250 \Omega \cdot e^{- j \cdot 53,13 ^{\circ}}}$

oder in Versorschreibweise:

$\boxed{ \underline{Z} = 250 \Omega \angle{-53,13 ^{\circ}} }$

wie gehts weiter?

Nachdem du jetzt weißt, was es mit dem Thema Symbolische Methode im komplexen Bereich auf sich hat, starten wir im kommenden Kurstext damit, dir die Leistung im komplexen Bereich zu erklären.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET6 (Wechselstromtechnik 1) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++