In diesem Kurstext stellen wir dir kurz das Thema Ohmsches Gesetz im komplexen Bereich vor und erklären dir, wie sich die komplexen Größen Strom und Spannung in diesem Zusammenhang verhalten und nutzen lassen um den komplexen Widerstand und den komplexen Leitwert für einen Ohmschen Widerstand, einen Kondensator und eine Spule zu ermitteln.

Ohmsches Gesetz – Überblick
Das Ohmsche Gesetz ist ja bekanntlich eines der einfachsten und gleichzeitig wichtigsten Grundgesetze in der Elektrotechnik. Egal ob Gleichstromtechnik oder Wechselstromtechnik, dieses Gesetz taucht immer wieder auf.
In der Allgemeinen Form hat es folgende Erscheinung:
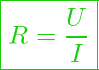 Ohmsches Gesetz für den Elektrischen Widerstand
Ohmsches Gesetz für den Elektrischen Widerstand
![]() Ohmsches Gesetz für die Elektrische Spannung
Ohmsches Gesetz für die Elektrische Spannung
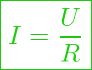 Ohmsches Gesetz für dir Elektrische Stromstärke
Ohmsches Gesetz für dir Elektrische Stromstärke
“Ziel dieses Kurstextes besteht darin, dir zu erklären wir dieses Gesetz im komplexen Bereich genutzt werden kann. Man spricht in diesem Zusammenhang vom Ohmschen Gesetz des Wechselstromkreises oder gelegentlich auch vom Ohmschen Gesetz der Wechselstromtechnik.”
Dazu müssen wir uns kurz vor Augen halten, wodurch sich eine komplexe Gleichung auszeichnet. Es müssen immer zwei voneinander nicht abhängige Aussagen erfüllt sein. Die Trennung der Aussagen erfolgt mit Hilfe von reellen Gleichungen für
- Zeigerlänge und Phasenwinkel
- Realteil und Imaginärteil.
Ohmsches Gesetz – Komplexer Widerstand
Bildet man den Quotienten aus elektrischer Spannung und elektrischen Strom, so erhält man daraus eine konstante Größe, die im Wechselstromkreis als komplexer Widerstand ![]() oder als Impedanz bezeichnet wird.
oder als Impedanz bezeichnet wird.
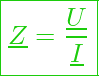
Auch diese konstante Größe lässt sich in der komplexen Ebene als Zeiger darstellen nur mit dem Unterschied, dass sie im Gegensatz zu Darstellung von komplexen Strom und komplexer Spannung als zeitunabhängige Größe nicht rotiert.
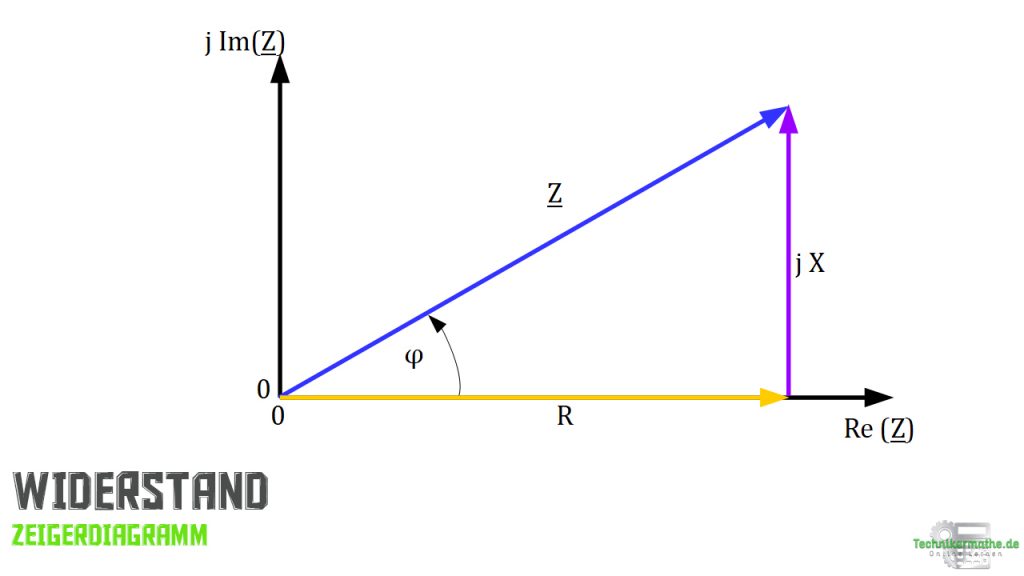
Wir unterscheiden wieder zwischen den beiden Ansätzen
Zeigerlänge und Phasenwinkel
Hier sieht die Gleichung wie folgt aus:
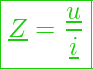
bzw.

Aus der Anpassung der Gleichung ergibt sich dann
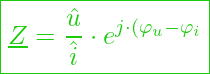
Realteil und Imaginärteil
Die Gleichung für den Realteil und den Imaginärteil hat folgende Erscheinung:
![]()
![]() ist der Wirkwiderstand (Resistanz),
ist der Wirkwiderstand (Resistanz), ![]() ist der Blindwiderstand (Reaktanz) und
ist der Blindwiderstand (Reaktanz) und ![]() ist der Scheinwiderstand.
ist der Scheinwiderstand.
Die Vorsilbe "Wirk" bezeichnet den Realteil und die Vorsilbe "Blind" drückt den Imaginärteil aus. Mit "Schein" beschreiben wir den Betrag der Größe.
Ohmsches Gesetz – Komplexer Leitwert
Bildet man den Kehrwert der Impedanz, so erhält man als Ergebnis den komplexen Leitwert. Diesen bezeichnet man auch als Admittanz oder Leitwertoperator.
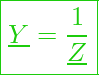
Diese Entspricht dann ebenfalls:
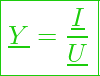
Zeigerlänge und Phasenwinkel
Hier sieht die Gleichung wie folgt aus:
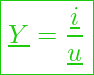
bzw.

Aus der Anpassung der Gleichung ergibt sich dann
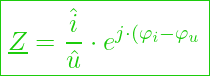
Realteil und Imaginärteil
Die Gleichung für den Realteil und den Imaginärteil hat folgende Erscheinung:
![]()
![]() ist der Wirkleitwert (Konduktanz),
ist der Wirkleitwert (Konduktanz), ![]() ist der Blindleitwert (Suszeptanz) und
ist der Blindleitwert (Suszeptanz) und ![]() ist der Scheinleitwert.
ist der Scheinleitwert.
Ohmsches Gesetz – Elektrische Bauteile
Jetzt schauen wir uns das ganze Mal für die drei bekannten elektrischen Bauteile Ohmsche Widerstand, Kondensator und Spule genauer an.
Ohmsches Gesetz – Ohmscher Widerstand
Verwenden wir in der Gleichung für den Ohmschen Widerstand anstelle von ![]() und
und ![]() Zeiger, so erhalten wir die Gleichung:
Zeiger, so erhalten wir die Gleichung:
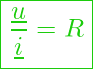
![]() ist ein reelle Größe. Aus diesem Grund gilt für die Phasenwinkel von Strom und Spannung
ist ein reelle Größe. Aus diesem Grund gilt für die Phasenwinkel von Strom und Spannung
![]()
Denn es gilt:
![]()
Da bedeutet, dass die Zeiger ![]() und
und ![]() die gleichen Nullphasenwinkel am Ohmschen Widerstand aufweisen und somit gleichphasig sind.
die gleichen Nullphasenwinkel am Ohmschen Widerstand aufweisen und somit gleichphasig sind.
Komplexer Widerstand am Ohmschen Widerstand (Ohmsches Gesetz)
Der zugehörige komplexe Widerstand hat dann die Form:
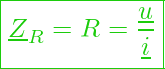
bzw.
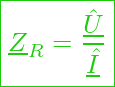
Oder in Versordarstellung:
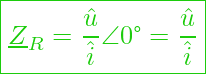
Komplexer Leitwert am Ohmschen Widerstand
Der zugehörige komplexe Leitwert hat dann die Form:
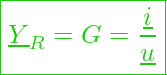
bzw.
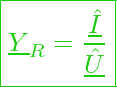
Oder in Versordarstellung:
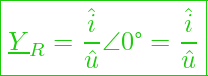
Ohmsches Gesetz – Kondensator
Verwenden wir in der Gleichung für die Kapazität (Kondensator) ![]() anstelle von
anstelle von ![]() und
und ![]() Zeiger, so erhalten wir nach der Differentiation die Gleichung:
Zeiger, so erhalten wir nach der Differentiation die Gleichung:
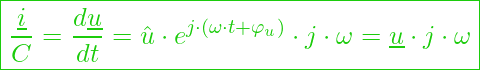
Jetzt kommt uns folgende Gleichung zur Hilfe:
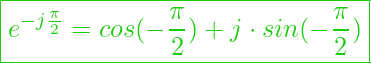
das ergibt dann:
![]()
und letztlich:
![]()
Nach der Umstellung der obigen Gleichung und dem Einsetzen von ![]() erhalten wir final
erhalten wir final

das entspricht

oder halt
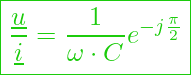
Aber was können wir jetzt damit anfangen? – Schauen wir uns die Phasenwinkel an:
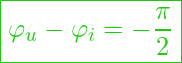
Denn es gilt:
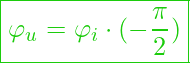
Es zeigt sich, dass die ![]() bei einem Kondensator (ideal) gegenüber
bei einem Kondensator (ideal) gegenüber ![]() um
um ![]() in der Phase verschoben ist.
in der Phase verschoben ist.
Komplexer Widerstand am Kondensator (Ohmsches Gesetz)
Für die Impedanz gilt dann:
![]()
oder in Versordarstellung:
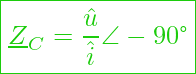
Schaut man jetzt wieder auf den Realteil und den Imaginärteil, so zeigt sich beim komplexen Widerstand ![]() am Kondensator, dass dieser nur aus einem negativen Imaginärteil besteht. Daher haben wir nur einen negativen Blindwiderstand und keinen Wirkwiderstand vorliegen.
am Kondensator, dass dieser nur aus einem negativen Imaginärteil besteht. Daher haben wir nur einen negativen Blindwiderstand und keinen Wirkwiderstand vorliegen.
Formal äußert sich das dann so:
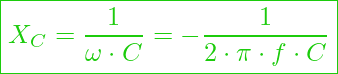
Komplexer Leitwert am Kondensator
Der zugehörige komplexe Leitwert (Admittanz) hat dann die Form:
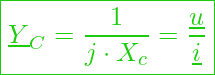
bzw.
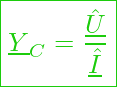
Oder in Versordarstellung:
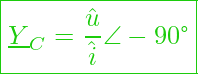
Formal äußert sich das dann so:
![]()
Ohmsches Gesetz – Spule
Verwenden wir in der Gleichung für die Induktivität (Spule) ![]() anstelle von
anstelle von ![]() und
und ![]() Zeiger, so erhalten wir nach der Differentiation die Gleichung:
Zeiger, so erhalten wir nach der Differentiation die Gleichung:
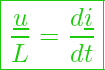
Das entspricht
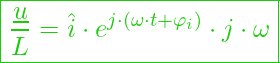
und angepasst erhalten wir:
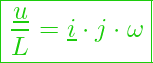
Jetzt kommt uns folgende Gleichung zur Hilfe:
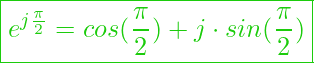
das ergibt dann letztlich:
![]()
Nach der Umstellung der obigen Gleichung und dem Einsetzen von ![]() erhalten wir final
erhalten wir final
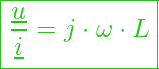
das entspricht ebenfalls

Aber was können wir jetzt erneut damit anfangen? – Schauen wir uns die Phasenwinkel an:
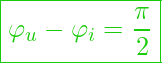
Denn es gilt:
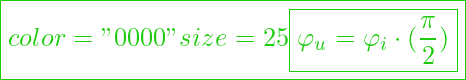
Es zeigt sich, dass die ![]() bei einer Spule (ideal) gegenüber
bei einer Spule (ideal) gegenüber ![]() um
um ![]() in der Phase voreilt ist.
in der Phase voreilt ist.
Komplexer Widerstand an der Spule (Ohmsches Gesetz)
Für die Impedanz gilt dann:
![]()
oder in Versordarstellung:
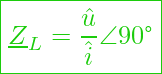
Schaut man jetzt wieder auf den Realteil und den Imaginärteil, so zeigt sich beim komplexen Widerstand ![]() an der Spule, dass dieser nur aus einem positiven Imaginärteil besteht. Daher haben wir nur einen positiven Blindwiderstand und keinen Wirkwiderstand vorliegen.
an der Spule, dass dieser nur aus einem positiven Imaginärteil besteht. Daher haben wir nur einen positiven Blindwiderstand und keinen Wirkwiderstand vorliegen.
Formal äußert sich das dann so:
![]()
Komplexer Leitwert am Kondensator
Der zugehörige komplexe Leitwert (Admittanz) hat dann die Form:
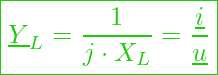
bzw.
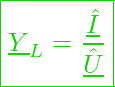
Oder in Versordarstellung:
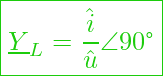
Formal äußert sich das dann so:
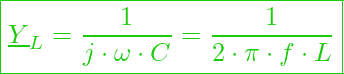
Was gibt es noch bei uns?
Was ist Technikermathe.de?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Interaktive Übungsaufgaben
Quizfrage 1
Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?
Auszüge aus unserem Kursangebot
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET6 (Wechselstromtechnik 1) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team









