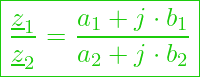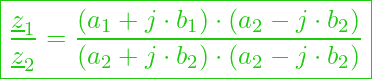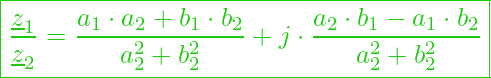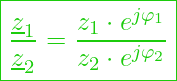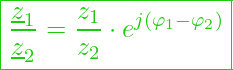(ET5-18) Komplexe Wechselstromschaltungen – Komplexe Zahlen

In diesem Kurstext stellen wir dir kurz die komplexen Zahlen vor und erklären dir, wie wir diese für die nachfolgenden komplexen Größen der Wechselstromtechnik nutzen.

Komplexe Zahlen – Überblick

Wir zeigen die wie Komplexe Zahlen uns helfen komplexe Berechnungen von Wechselstromschaltungen durchzuführen. Damit ist es uns möglich komplexe Spannungen, Ströme, Widerstände und Leitwerte zu ermitteln.

Komplexe Zahlen – Regeln

Wie du bereits weißt, nutzen wir die komplexen Zahlen um komplexe Netzwerke der Wechselstromtechnik zu lösen. Hierbei beschreiben wir die Größen mit komplexen Zahlen. Nachfolgend zeigen wir dir zuerst die Darstellung im Zeigerdiagramm auf und gehen anschließend auf die mathematische Darstellung im Detail ein.

Geometrische Ansicht

“Für die Darstellung der komplexen Zahlen bedienen wir uns der Gaußschen Zahlenebene.”

Im Koordinatensystem teilen wir die Achsen ein in eine reelle Achse (Abzissenachse) und in eine imaginäre Achse (Ordinatenachse). Wie das aussieht, kannst du in der nächsten Abbildung nachvollziehen.

Komplexe Zahlen - Gaußsche Zahlenebene — Komplexe Zahlen – Gaußsche Zahlenebene

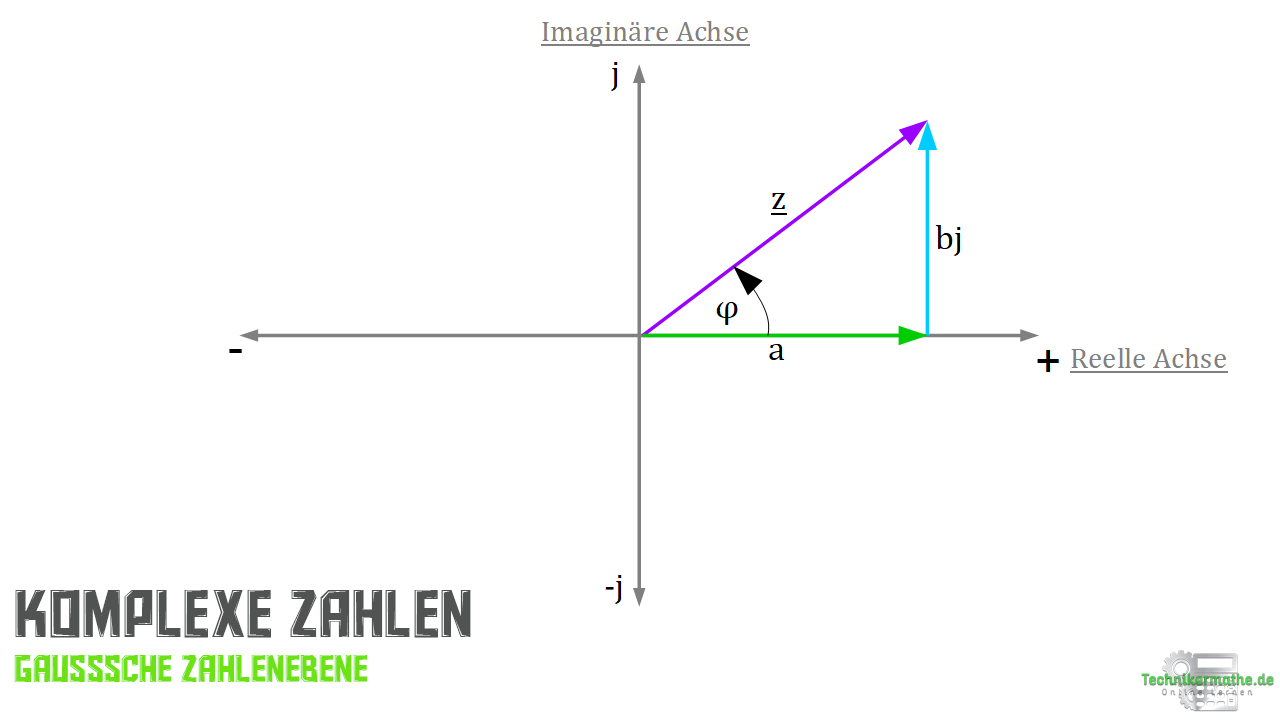
Auf der reellen Achse tragen wir die reellen Zahlen ab.

Als imaginäre Einheit wählen wir die Zahl (Buchstaben) j. Deren Quadrat ergibt den Wert $- 1$ . Formal äußert sich das wie folgt:

$\boxed{ j = \sqrt{-1} }$ – Imaginäre Einheit.

undefiniert

Gute Frage...

Falls du dich jetzt fragst, warum wir hierfür nicht wie in der allgemeinen Mathematik ein $i$ verwenden, dann liegt das daran, dass $i$ bereits für die komplexe Stromstärke in der Wechselstromtechnik reserviert ist und wir somit ausweichen müssen um Verwechslungen vorzubeugen.

Merk's dir!

Bei der Gaußschen Zahlenebene gilt, dass jeder Punkt durch einen Zeiger dargestellt wird. Dieser schließt zusammen mit der reellen Achse den Winkel $\varphi$ ein. Daraus können wir ebenfalls ableiten, dass jede komplexe Zahl einem Zeiger entspricht, welcher im Achsenursprung startet und bis zum zugehörigen Punkt zeigt.

Damit wir den Überblick zwischen reellen und komplexen Größen behalten, unterstreichen wir die komplexen Größen.

Komplexe Zahlen – Darstellungen

“Im Folgenden verwenden wir immer $\underline{z}$

als Stellvertreter für die komplexen Wechselgrößen $\underline{u}$

und $\underline{i}$

“

Komplexe Zahlen können auf unterschiedliche Weise dargestellt werden. So kann jede komplexe Zahl $\underline{z}$ durch folgende Gleichung beschrieben werden:

$\boxed{ \underline{z} = a + j \cdot b }$

wobei

$\boxed{ a, b \in R }$

Kennzahlen:

$\boxed{j = }$ Imaginäre Zahl

$\boxed{a = }$ Realteil ( $Re(\underline{z})$ ) von $\underline{z}$

$\boxed{b = }$ Imaginärteil ( $Im(\underline{z})$ ) von $\underline{z}$

Merk's dir!

Nimmt $b$ den Wert null an, also $b = 0$ , so erhalten wir als Ergebnis die reellen Zahlen als Sonderfall der komplexen Zahlen.

Algebraische Form der Darstellung

Die algebraische Form nutzt die kartesischen Koordinaten und sieht wie folgt aus:

$\boxed{ \underline{z} = a + j \cdot b }$

Hier ist $\underline{z}$ ein Punkt mit einer Abszisse a und einer Ordinate b.

Trigonometrische Form der Darstellung

Die trigonometrische Form nutzt die Polarkoordinaten und sieht wie folgt aus:

$\boxed{ \underline{z} = z \cdot (cos \varphi + j \cdot sin \varphi) }$

Hier wird $\underline{z}$ durch einen Zeiger mit der Länge $z$ dargestellt. Zwischen dem Zeiger und der Abszissenachse liegt der Winkel $\varphi$ .

Hier gilt für $z$

$\boxed{ z = |\underline{z}| = \sqrt{a^2 + b^2}}$ – Betrag der komplexen Zahl

sowie

$\boxed{ \varphi = arctan \frac{b}{a}}$ – Argument der komplexen Zahl

Exponentialform der Darstellung

Die Exponentialform bedient sich der Eulerschen Formel und sieht wie folgt aus:

$\boxed{\underline{z} = z \cdot e^{j\varphi} }$

mit

$\boxed{ e^{j\varphi} = cos \varphi + j \cdot sin \varphi }$ – Eulersche Formel

Merk's dir!

Für komplexe Zahlen sind Überlegungen wie im Vergleich kleiner oder größer nicht definiert. Sie können laut Definition lediglich gleich sein, wenn ihre jeweiligen Realteile und Imaginärteile identisch sind.

Komplexe Konjugation

In der nachfolgenden Abbildung kannst du erkennen, dass ein Vorzeichenwechsel stattgefunden hat und somit der Zeiger an der reellen Achsen gespiegelt wurde.

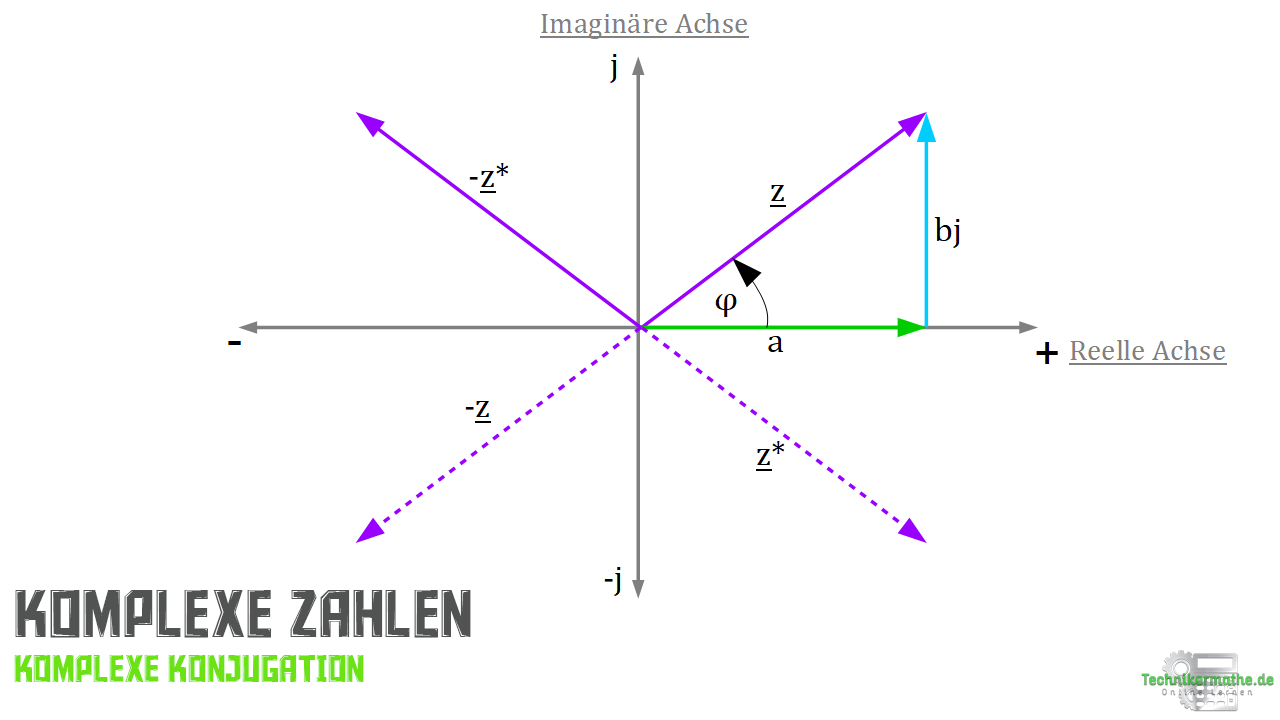
Dies geschieht, weil wir das Vorzeichen des Imaginärteils geändert haben. Dadurch wird $\underline{z}$ zu der konjugierten komplexen Zahl $\underline{z}*$ :

$\boxed{ \underline{z}* = a - j \cdot b }$ konjugiert komplexe Zahl der algebraischen Form

oder

$\boxed{ \underline{z}* = z \cdot e^{-j \varphi} }$ konjugiert komplexe Zahl der Exponentialform

Führt man nun noch zwei Mal eine Konjugation durch, so erhält man wieder den ursprünglichen Wert.

$\boxed{(\underline{z}*)* = \underline{z} }$

Abschließend noch eine weitere Gegebenheit: Wenn man das Produkt aus der anfänglichen Zahl und der konjugierten Zahl bildet, so ergibt das das Quadrat des Betrags der komplexen Zahl:

$\boxed{ \underline{z} \cdot \underline{z} = (a + j \cdot b)(a - j \cdot b) = a^2 + b^2 = |\underline{z}|^2 }$

Siehst du die Analogie zu den Binomischen Formeln?

Komplexe Zahlen – Rechnungen

Nachfolgend findet du die üblichen Rechnenoperationen, die man für die komplexen Zahlen der Wechselgrößen verwendet. Die Menge, die wir als Ergebnis erhalten bildet einen “Körper” den wir mit $C$ bezeichnen.

Addition und Subtraktion

Wie du vermutlich bereits erahnen kannst, verhalten sich die komplexen Zahlen wie Vektoren in einem zweidimensionalen Feld.

” Daher können wir bei der Addition und Subtraktion von komplexen Zahlen wie bei der Vektoraddition vorgehen.”

In der nächsten Abbildung siehst du die Darstellung der Vektoraddition bezogen auf unsere komplexen Zahlen:

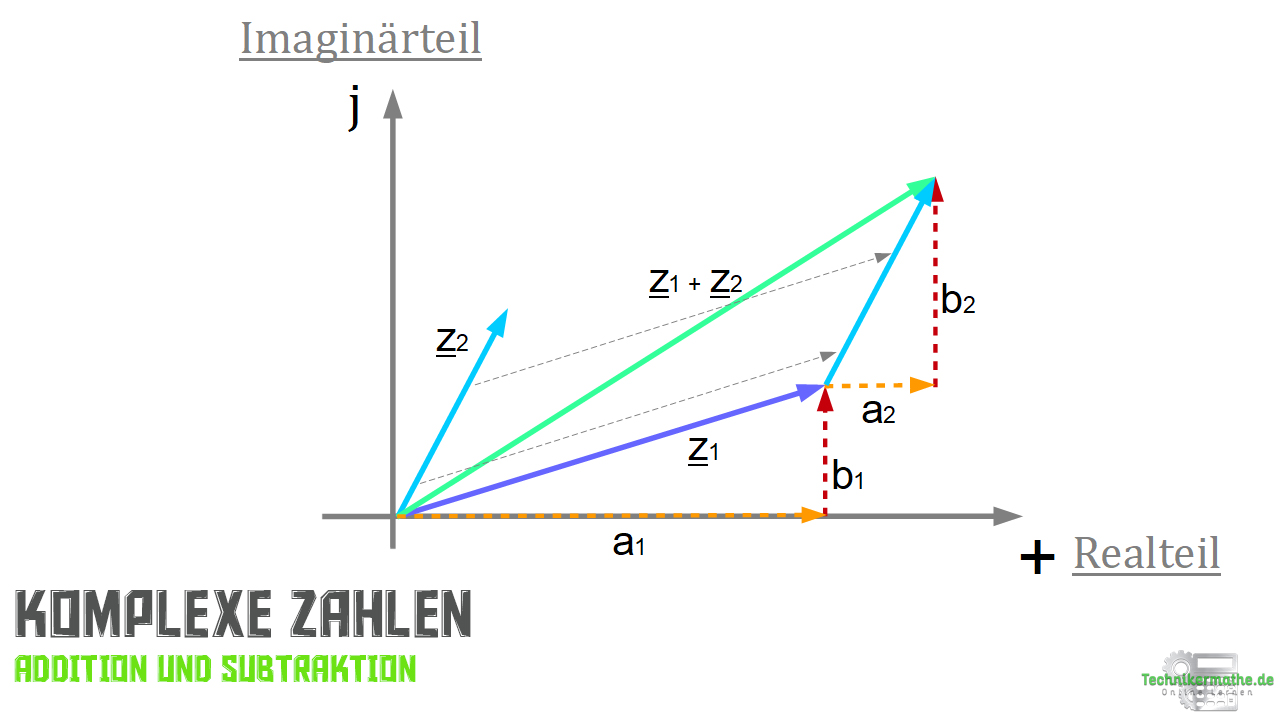
Die Berechnung der Real- und Imaginärteile erfolgt getrennt:

Komplexe Zahlen – Addition

$\boxed{ \underline{z}_1 + \underline{z}_2 = (a_1 + j \cdot b_1) + (a_2 + j \cdot b_2) }$

Ausklammern der Imaginären Zahl $j$ und anpassen von Real- und Imaginärteil (a, b) ergibt dann:

$\boxed{ \underline{z}_1 + \underline{z}_2 = (a_1 + a_2) + j \cdot (b_1 + b_2) }$

Komplexe Zahlen – Subtraktion

$\boxed{ \underline{z}_1 - \underline{z}_2 = (a_1 + j \cdot b_1) - (a_2 + j \cdot b_2) }$

Ausklammern der Imaginären Zahl $j$ und anpassen von Real- und Imaginärteil (a, b) ergibt dann:

$\boxed{ \underline{z}_1 + \underline{z}_2 = (a_1 - a_2) + j \cdot (b_1 - b_2) }$

Multiplikation und Division

Die Vorgehensweise bei der Multiplikation und Division für komplexe Zahlen erfolgt anders.

“Hier werden die Winkel $\varphi$

zwischen der Zeiger zur Ordinate addiert.”

In der nächsten Abbildung siehst du die Darstellung der Multiplikation im Zeigerbild bezogen auf unsere komplexen Zahlen:

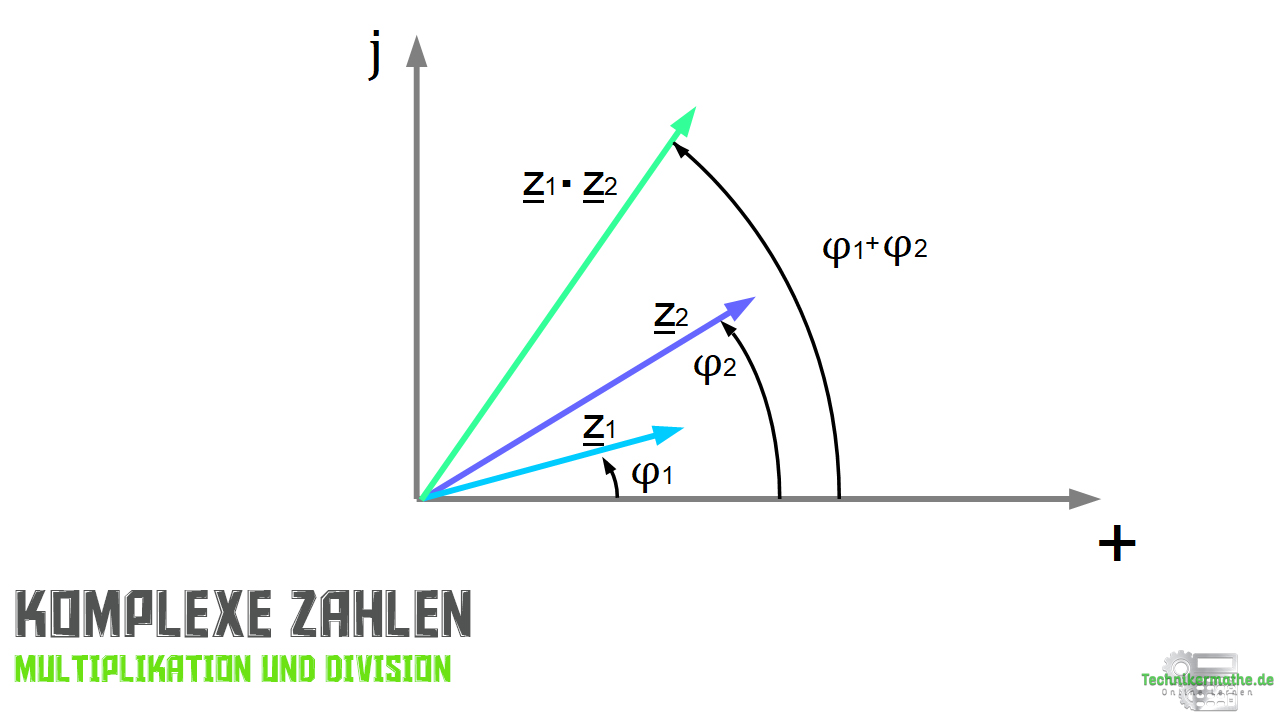
Komplexe Zahlen – Multiplikation

Wollen wir eine komplexe Zahl mit einer anderen komplexen Zahl multiplizieren, dann gelten folgende Gleichungen:

Für die algebraische Form gilt:

$\boxed{ \underline{z}_1 \cdot \underline{z}_2 = (a_1 + j \cdot b_1) \cdot (a_2 + j \cdot b_2) }$

Ausklammern der Imaginären Zahl $j$ und anpassen von Real- und Imaginärteil (a, b) ergibt dann:

$\boxed{\underline{z}_1 + \underline{z}_2 = (a_1 \cdot a_2 - b_1 \cdot b_2) - j \cdot (a_1 \cdot b_2 + b_1 \cdot a_2) }$

Für die Exponentialform gilt:

$\boxed{ \underline{z}_1 \cdot \underline{z}_2 = z_1 \cdot e^{j \varphi_1} \cdot z_2 \cdot e^{j \varphi_2} }$

Ausklammern der Imaginären Zahl $j$ in den Exponenten ergibt:

$\boxed{ \underline{z}_1 \cdot \underline{z}_2 = z_1 \cdot z_2 \cdot e^{ j(\varphi_1+ \varphi_2)}}$

Merk's dir!

In der obigen Abbildung und mit Blick auf die Gleichungen zeigt sich, dass bei der Multiplikation von $\underline{z}_1$ und $\underline{z}_2$ der Zeiger $\underline{z}_1$ mit dem Faktor $z_2 = |\underline{z}_2|$ verlängert wird und gleichzeitig um den Winkel $\varphi_2$ gedreht wird. Hier bei erfolgt die Drehung gegen den Uhrzeigersinn also in positive Drehrichtung einer elektrischen Wechselgröße.

Komplexe Zahlen – Division

Wollen wir eine komplexe Zahl durch eine andere komplexe Zahl dividieren, dann gelten folgende Gleichungen:

Für die algebraische Form gilt:

$\boxed{ \frac{\underline{z}_1}{\underline{z}_2} = \frac{a_1 + j \cdot b_1}{a_2 + j \cdot b_2} }$

Die Brucherweiterung ergibt:

$\boxed{ \frac{\underline{z}_1}{\underline{z}_2} = \frac{(a_1 + j \cdot b_1) \cdot (a_2 - j \cdot b_2)}{(a_2 + j \cdot b_2) \cdot (a_2 - j \cdot b_2)} }$

Ausklammern der Imaginären Zahl $j$ ergibt:

$\boxed{ \frac{\underline{z}_1}{\underline{z}_2} = \frac{a_1 \cdot a_2 + b_1 \cdot b_2}{a_2^2 + b_2^2} + j \cdot \frac{a_2 \cdot b_1 - a_1 \cdot b_2}{a_2^2 + b_2^2} }$

Für die Exponentialform gilt:

$\boxed{\frac{\underline{z}_1}{\underline{z}_2} = \frac{z_1 \cdot e^{j \varphi_1}}{z_2 \cdot e^{j \varphi_2}}}$

Ausklammern der Imaginären Zahl $j$ in den Exponenten ergibt:

$\boxed{ \frac{\underline{z}_1}{\underline{z}_2} = \frac{z_1}{z_2} \cdot e^{j (\varphi_1 - \varphi_2)} }$

Merk's dir!

In der obigen Abbildung und mit Blick auf die Gleichungen zeigt sich, dass bei der Division von $\underline{z}_1$ und $\underline{z}_2$ der Zeiger $\underline{z}_1$ um den Winkel $\varphi_2$ gedreht wird. Hier bei erfolgt die Drehung aber im Uhrzeigersinn also in negative Drehrichtung einer elektrischen Wechselgröße. Zudem verkürzt sich die Länge des Zeigers um den Faktor $\frac{1}{z_2}$

Komplexe Zahlen – Zusammenfassung

Aus diesem Kurstext zum Thema komplexe Zahlen solltest du für die weiteren Kurstext folgendes im Gedächtnis behalten:

Jede komplexe Zahl entspricht einem Zeiger in der Gaußschen Zahlenebene
Komplexe Zahlen kann man auf dreierlei Weise beschreiben: algebraische Form, trigonometrische Form & Exponentialform.
a ist der Realteil und b der Imaginärteil der komplexen Zahlen
$|\underline{z}| = z$ ist der Betrag für komplexe Zahlen $\underline{z}$
$\varphi$ ist das Argument für komplexe Zahlen
$\underline{z}*$ ist das Konjugierte der komplexen Zahl $\underline{z}$
Die Multiplikation von $\underline{z}$ und $\underline{z}*$ ergibt: $\underline{z} \cdot \underline{z}* = |\underline{z}|²$
Alle vier Grundrechenarten können für die komplexen Zahlen genutzt werden.

undefiniert

Was nehme ich wofür?...

In den meisten Fällen verwendet man die Addition und Subtraktion von komplexen Zahlen die algebraische Form und für die Multiplikation und Division die Exponentialform.

wie gehts weiter?

Nachdem du jetzt weißt, was es mit dem Thema komplexe Zahlen auf sich hat, starten wir im kommenden Kurstext damit, dir die Komplexe Spannung und den komplexen Strom zu erklären.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET6 (Wechselstromtechnik 1) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++