(ET5-17) Komplexe Wechselstromschaltungen – Anwendung

In diesem Kurstext gehen wir auf die Anwendung für die komplexe Wechselstromrechnung ein und stellen dir hier schon mal die Regeln und Größen für die Berechnungen in den kommenden Kurstexten vor.

Im Vorherigen Kurstext hast du bereits den möglichen Aufbau einer komplexen Wechselstromschaltung kennengelernt. Zur Erinnerung hier noch mal die zugehörige Abbildung:

Komplexe Wechselstromschaltung, komplexe Wechselstromrechnung

Komplexe Wechselstromrechnung – Schreibweisen

Damit du auch die komplexe Wechselstromrechnung richtig verstehst, sollten dir der Umgang mit den komplexen Zahlen und die Berechnung von elektrischen Netzwerken bekannt sein. Ersteres erlernst du noch mal im nachfolgenden Kurstext und letzteres sollte dir ohnehin bekannt sein.

Falls dir die Regeln zur Reihen- und Parallelschaltung, sowie der Maschensatz und Knotensatz von Kirchhoff nicht mehr so geläufig sind, dann schaue dir bitte noch mal die vorherigen Kursabschnitte genau an.

Die komplexe Wechselstromrechnung befasst sich mit zeitlich veränderlichen Spannungen und Strömen, die einen sinusförmigen Verlauf im Zeitdiagramm aufweisen.

Damit wir genau wissen, dass es sich um eine Veränderlichkeit und nicht um zeitlich fixe Größen handelt, formulieren dir die Augenblickswerte. Diese zeitlich veränderlichen Werte kennzeichnen wir immer mit Kleinbuchstaben:

$\boxed{i = }$ Elektrischer Strom

$\boxed{u = }$ Elektrische Spannung

” Der Wert für den elektrischen Widerstand hingegen, ist zeitlich nicht veränderlich und wird weiterhin mit einem Großbuchstaben angegeben.”

$\boxed{R = }$ Elektrischer Widerstand

Damit wir auch nicht den Fehler begehen diese Werte mit anderen Werten zu vertauschen, kennzeichnen wir zusätzlich die Zeitabhängigkeit damit, dass wir sie für den Strom und die Spannung angeben. Dies erfolgt über runde Klammern die den Buchstaben t (Zeit) umklammern.

$\boxed{i (t) = }$ Elektrischer Strom in Zeitabhängigkeit

$\boxed{u (t) = }$ Elektrische Spannung in Zeitabhängigkeit

” Auch hier gilt wieder für den elektrischen Widerstand, dass keine Angabe für die Zeitabhängigkeit erfolgt”

$\boxed{R = }$ Elektrischer Widerstand ohne Zeitabhängigkeit

Die Formelzeichen von komplexen Größen werden durch einen Unterstrich eindeutig gekennzeichnet.

Damit es nicht zur Verwechslungen mit dem zeitabhängigen Strom $i$ kommt, verwenden wir für die imaginäre Einheit den Buchstaben $j$ für den gilt $j^2 = - 1$ .

Komplexe Wechselstromrechnung – Bedingungen

Bevor wir jetzt wahllos loslegen und alles berechnen was uns vor die “Flinte” kommt. Müssen wir uns zuerst die Bedingungen anschauen, die für die komplexe Wechselstromrechnung gelten.

Eine komplexe Wechselstromrechnung gilt nur für ein linear zeitinvariantes System. Hier muss gewährleistet sein, dass sich der Überlagerungssatz anwenden lässt.

Es gilt daher, dass alle elektrischen Bauteile, unabhängig davon, ob es sich jetzt um Widerstände, Spulen (Induktivitäten) oder Kondensatoren (Kapazitäten) handelt, lineare Eigenschaften im vorliegenden Frequenzbereich besitzen.

Ausgeschlossen werden müssen daher Spulen bei denen eine magnetische Sättigung eintritt oder Kondensatoren (zumeist Plattenkondensatoren) bei denen das Dielektrikum von der elektrischen Feldstärke beeinflusst wird.

Zudem sind auch elektrische Bauteile wie Modulatoren und Gleichrichter von der komplexen Wechselstromrechnung ausgeschlossen, da sie auf einer Nichtlinearität beruhen und somit kein sinusfömiges Verhalten aufweisen.

Halbleiterelemente können ebenfalls nicht mit dieser Rechnung abgebildet werden, ausgenommen sind Fälle in denen die Kennlinie linearisiert werden kann und sie somit für die komplexe Wechselstromrechnung anwendbar werden. Stichwort: Zweitorttheorie für Transistorschaltungen.

Komplexe Wechselstromrechnung – Einschränkungen

Auch wenn die obigen Bedingungen allesamt erfüllt sind, so gibt es Einschränkungen, die wir beachten müssen.

Bei der komplexen Wechselstromrechnung gehen wir immer von einer sinusförmigen elektrischen Größe aus. Hier muss jedoch darauf geachtet werden, dass das Einschalten und das damit einhergehende Einschwingen der Frequenz so lange zurückliegen, dass es keinen Einfluss mehr auf das Verhalten des Systems gibt.

Ein System mit sinusförmigen Größen ist immer nur dann eingeschwungen, wenn jede dieser Größen die gleiche Kreisfrequenz aufweist. Also $\omega = 2 \cdot \pi \cdot f$ .

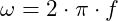Wir können nur den stationären Zustand, jedoch nicht den flüchtigen Einschaltvorgang berechnen. Somit sind Berechnungen zum Zeitpunkt eines Ein- und Ausschaltens nicht möglich.

Auch das Systemverhalten bei einzelnen Impulsen oder mehreren Impulsfolgen können nicht mit der komplexen Wechselstromrechnung untersucht werden. Abhilfe können hier nur noch die Laplace-Transformation und die Fourierreihen schaffen.

Obwohl wir uns ab jetzt lediglich auf elektrische Spannungen und Ströme beschränken, können wir unsere Aussagen bedingt auch auf andere physikalische Größen übertragen.

Komplexe Wechselstromrechnung – Einführung

Wie dir ja bekannt ist, schauen wir uns fast immer das Verhältnis von elektrische Stromstärke zur elektrischen Spannung innerhalb eines Stromkreise an.

Deren Verhältnisse können, sofern zumindest eine der Größen zeitlich konstant ist, entweder einen Rückschluss auf den elektrischen Widerstand oder den elektrischen Leitwert in einem Netzwerk liefern.

“Dabei unterscheiden wir ob die elektrische Spannung U konstant ist und der elektrische Strom I bestimmt werden muss, oder ob der umgekehrte Fall vorliegt.”

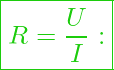$\boxed{ R = \frac{U}{I} : }$ Elektrischer Widerstand

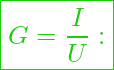$\boxed{G = \frac{I}{U} : }$ Elektrischer Leitwert

Soweit ist all das wirklich nichts neues für dich.

Auch das in der Wechselstromtechnik mit zeitlich veränderlichen Spannungen und Strömen gerechnet wird, die zudem einen sinusförmigen Verlauf besitzen, ist dir seit Beginn dieses Kurses bekannt.

Diese Veränderlichkeit drücken wir durch die Momentanwerte aus und grenzen sie damit von den zeitlich fixen Größen ab. Wie diese dargestellt werden, hast du ja oben erfahren.

Für einen ordentlichen Überblick hier noch mal die Gleichungen der passiven, linearen Elemente zur Bestimmung der Änderung der elektrischen Stromstärke und Spannung:

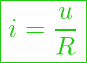$\boxed{i = \frac{u}{R} }$ – Stromstärke bei einen elektrischen Widerstand – verhält sich proportional zur Spannung.

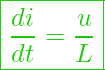$\boxed{ \frac{d i }{d t} = \frac{u}{L} }$ – Stromstärke bei einer Spule (Induktivität) – Änderung der Stromstärke verhält sich proportional zur Spannung.

alternativ geht auch:

$\boxed{i \cdot L = \int u \cdot dt }$

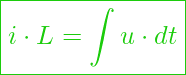
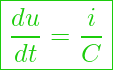$\boxed{\frac{d u}{d t} = \frac{i}{C} }$ Spannung bei einem Kondensator (Kapazität) – Änderung der Spannung verhält sich proportional zur Stromstärke.

alternativ geht hier auch:

$\boxed{ u \cdot C = \int i \cdot dt }$

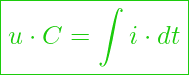
Wir ziehen den Rückschluss, dass wenn die Spannung oder die Stromstärke konstant ist, so ist auch die resultierenden Größe bei einem rein ohmschen Stromkreis konstant. – Hier befinden wir uns im Geltungsbereich der Gleichstromrechnung. Diese Konstanz liegt nicht beim Ein- oder Ausschalten vor.

haben wir weder einen Einschalt- noch einen Ausschaltvorgang gegeben, so stellt

die ideale Induktivität einen Kurzschluss des Stromzweiges

sowie

die ideale Kapazität eine Unterbrechung des Stromzweiges

darstellen.

Komplexe Wechselstromrechnung – Ab wann nötig?

” Die komplexe Wechselstromrechnung brauchen wir immer ab dem Zeitpunkt, ab welchem wir ein Netzwerk gegeben haben, in dem die vorgegebene Größe nicht mehr konstant oder der Stromkreis kein rein ohmsches Verhalten mehr zeigt. “

Denn jetzt haben wir eine komplizierte Strom-Spannungs-Beziehung vorliegen. Daraus resultiert, dass eine Kapazität oder eine Induktivität ab jetzt über Differentialgleichungen in die Berechnung eingehen. Formulierte Sonderfälle vereinfachen uns diese Berechnung aber.

Zu den Sonderfällen zählen Netzwerke in denen die vorgegebene Größen einen sinusförmigen periodischen Verlauf aufweist:

$\boxed{i (t) = \hat{i} \cdot sin( \omega \cdot t + \varphi_i) }$ – Sinusförmiger Wechselstrom

$\boxed{u (t) = \hat{u} \cdot sin( \omega \cdot t + \varphi_u) }$ – Sinusförmige Wechselspannung

Kennzahlen:

$\boxed{\hat{u} = }$ Maximalwert der Spannung

$\boxed{\hat{i} = }$ Maximalwert des Stroms

$\boxed{\omega = 2 \cdot \pi \cdot f = }$ Kreisfrequenz

$\boxed{\varphi_u = }$ Nullphasenwinkel der Spannung

$\boxed{\varphi_i = }$ Nullphasenwinkel des Stroms.

Der Phasenverschiebungswinkel ergibt sich aus der Differenz: $\varphi_u - \varphi_i$

Komplexe Wechselstromrechnung - Sinusspannung und Sinusstrom — Komplexe Wechselstromrechnung – Sinusspannung und Sinusstrom (Hier mit Effektivwerten dargestellt)

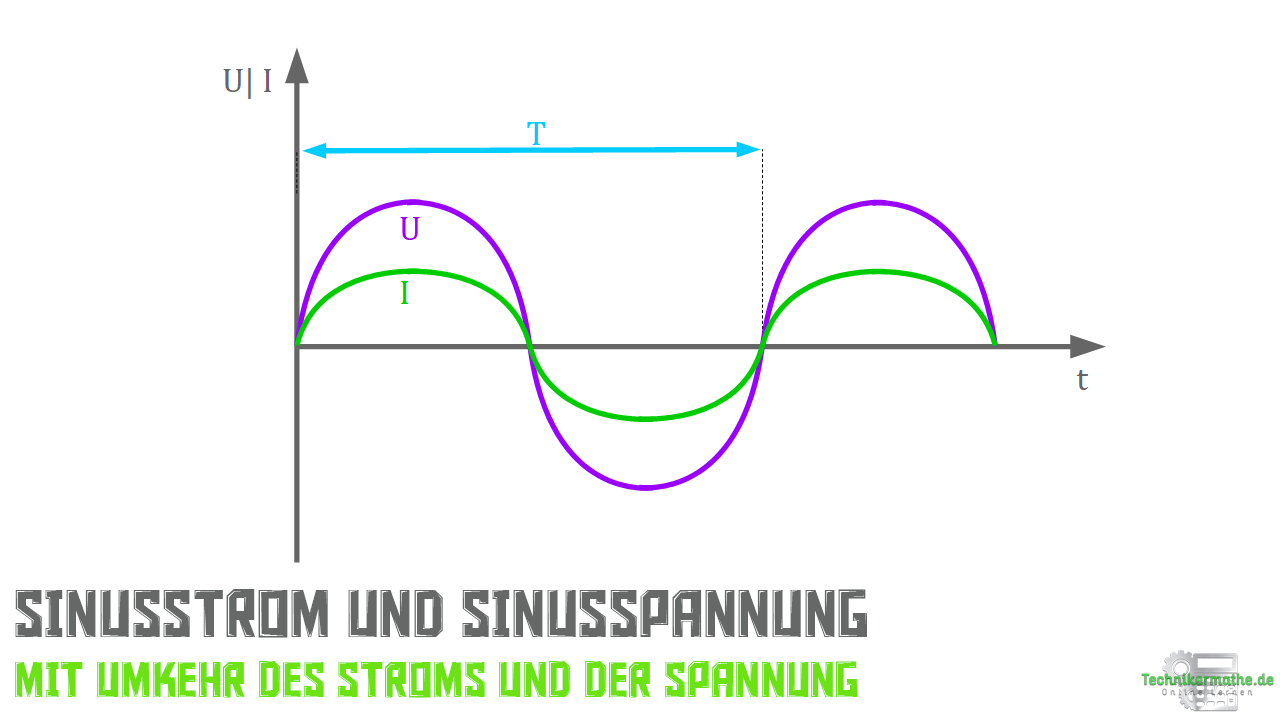
Obwohl sich die einstellende Größe in der Phasenverschiebung und dem Amplitudenverhältnis mit der Frequenz verändern kann, besitzt sie trotzdem einen periodischen Verlauf mit gleicher Frequenz.

wie gehts weiter?

Nachdem du jetzt weißt, was es mit dem Thema komplexe Wechselstromrechnung auf sich hat, starten wir im kommenden Kurstext damit, dir die Grundlagen der komplexen Zahlen als Vorarbeit für spätere Berechnungen zu vermitteln.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema Komplexe Wechselstromrechnung gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ET6 (Wechselstromtechnik 1) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++