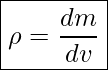Nun wenden wir uns der Mengenbilanz zu und erklären dir was du als Techniker dafür wissen musst. Mit Hilfe der Mengenbilanz kannst du fundierte Aussagen zu vielen Prozessen treffen.

Mengenbilanz – Grundsätzliches
Die Bestimmung dieser Größe setzt ein paar Grundsätze voraus:
- Die Größe des betrachteten Gebiets
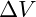 muss im Untersuchungszeitraum konstant bleiben.
muss im Untersuchungszeitraum konstant bleiben.
sowie
- Das System muss homogen sein, Inhomogenitäten verursachen Messungenauigkeiten.
sowie
- Die Mengenkonzentration innerhalb des Untersuchungsgebiets wird als stetige Funktion beschrieben.
Mengenbilanz – Bilanzraum
In der nächsten Abbildung findest du einen Bilanzraum mit den eingetragenen Größen:
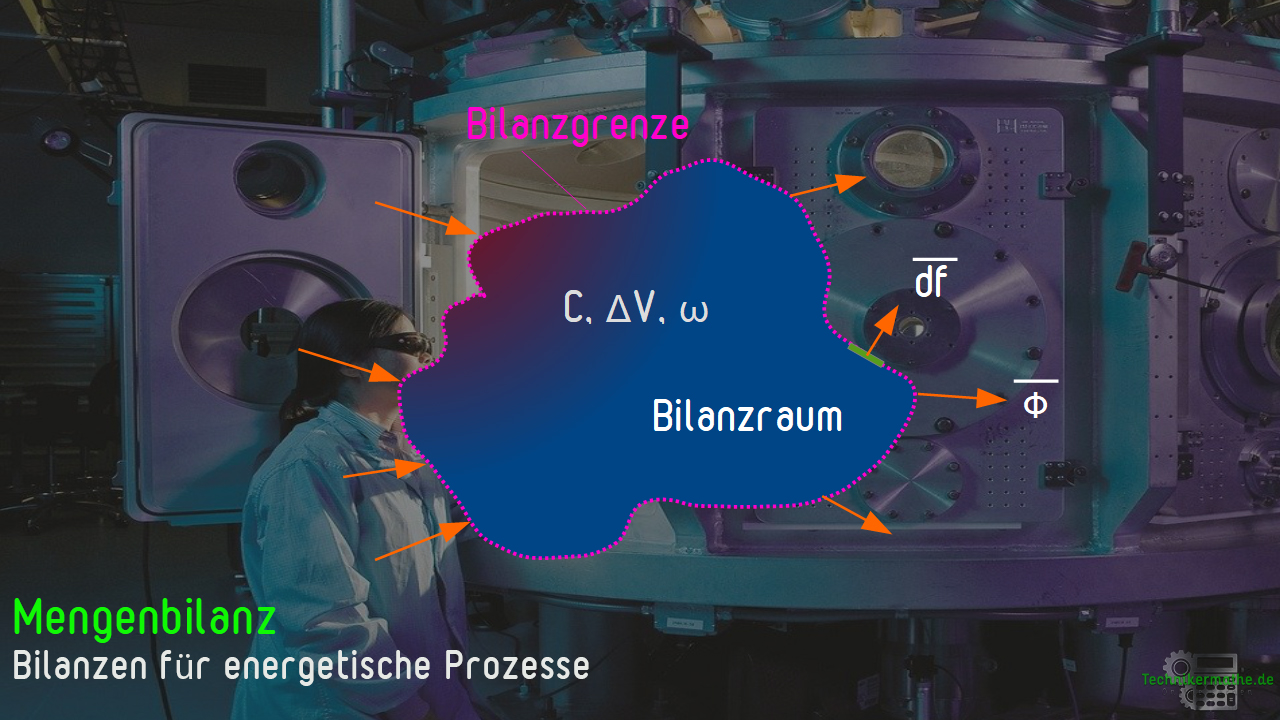
Mengenbilanz – Integrale Darstellung
Sind Punkt 1-3 erfüllt so erhalten wir für unseren Bilanzraum ![]() als integrale Darstellung:
als integrale Darstellung:
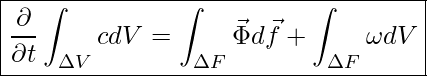
Kennzahlen:
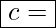 Mengenkonzentration für c(x, y, z)
Mengenkonzentration für c(x, y, z)
sowie
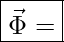 Mengenstromdichte, die austritt aus
Mengenstromdichte, die austritt aus 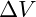 durch
durch 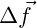
sowie
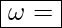 Umwandlungsrate pro Zeit und Volumeneinheit
Umwandlungsrate pro Zeit und Volumeneinheit
Eine integrale Darstellung ist zumeist rechenaufwendiger als eine differentielle Darstellung.
Mengenbilanz – Differentielle Darstellung
Aus diesem Grund wenden wir den Gauß’schen Satz an und erhalten als differentielle Gleichung als Ableitung:
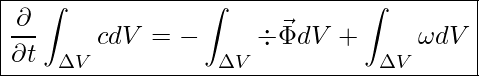
Diese differentielle Gleichung hat einen universellen Charakter, womit sie sich auf jedes Volumenelement anwenden lässt.
Mengenbilanz – partielle Differentialgleichung
Folglich bleibt es nur noch der Transfer zu einer partielle Differentialgleichung:
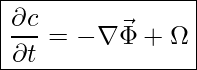
In dieser Darstellung besteht für die Größen ![]() und
und ![]() nur noch eine Abhängigkeit von der Zeit und den Ortskoordinaten. Um Abhängigkeiten zu reduzieren verwendet man die partielle (teilweise) Ableitung.
nur noch eine Abhängigkeit von der Zeit und den Ortskoordinaten. Um Abhängigkeiten zu reduzieren verwendet man die partielle (teilweise) Ableitung.
Davon ausgehend, dass für die Mengenkonzentration c eine Ortsunabhängigkeit vorliegt, vereinfacht sich unsere Gleichung zu:
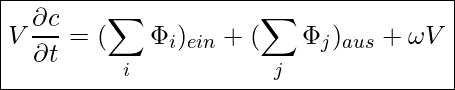
Kennzahlen:
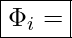 in das Gebiet eintretender Strom
in das Gebiet eintretender Strom
sowie
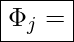 aus dem Gebiet austretender Strom
aus dem Gebiet austretender Strom
sowie
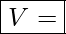 Gebiet
Gebiet
Dass die Umwandlungsrate ![]() und die Konzentration
und die Konzentration ![]() nur schwach ortsabhängig sind, erlaubt es uns entsprechende Mittelwerte
nur schwach ortsabhängig sind, erlaubt es uns entsprechende Mittelwerte ![]() zu bilden, die wir dann anstelle von
zu bilden, die wir dann anstelle von ![]() verwenden:
verwenden:
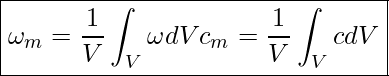
Kennzahlen:
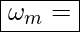 Mittelwert der Umwandlungsrate
Mittelwert der Umwandlungsrate
sowie
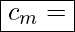 Mittelwert der Konzentration
Mittelwert der Konzentration
Materialbilanzgleichung
Nun betrachten wir die Materialbilanz im Detail.

In der Materialbilanzgleichung kommt die Relation von Mengenkonzentration sowie Mengenstromdichte zum Ausdruck:
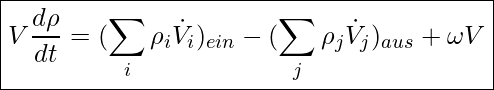
dabei entsprechen
sowie
Bilanzgleichung der Massenströme
Abschließend schauen wir uns noch die Gleichung für die Bilanzierung von Massenströmen an.

Nachdem wir nun sehr viel Vorarbeit geleistet haben, können wir nun die Massenströme bilanzieren. Hierzu definieren wir im ersten Schritt die Masse:
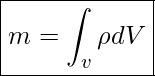
und anschließend stellen wir die Bilanz für die Massenströme auf.
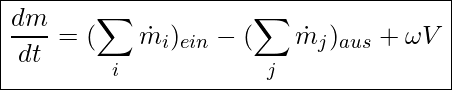
Was gibt es noch bei uns?
Was ist Technikermathe.de?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Interaktive Übungsaufgaben
Quizfrage 1
Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?
Auszüge aus unserem Kursangebot
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
ENT3 (Energetische Berechnungen) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++
Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++
Technikermathe.de meets Social-Media
Dein Technikermathe.de-Team