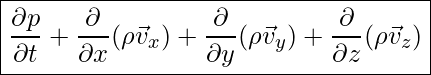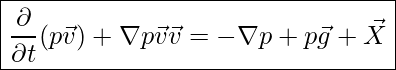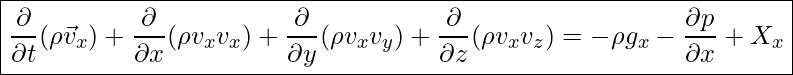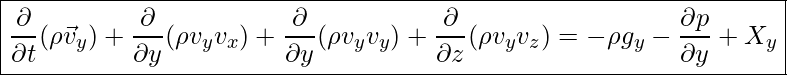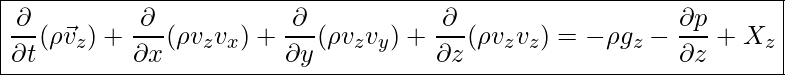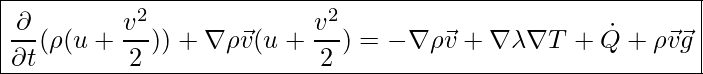(ENT2 30) – Erhaltungsgleichungen energetischer Prozesse

In diesem Kurstext erklären wir dir als angehenden Techniker ausführlich die Erhaltungsgleichung energetische Prozesse.

Erhaltungsgleichungen - Impuls — Erhaltungsgleichungen – Impuls

undefiniert

Noch einen Nachschlag? - Nein, danke! Lieber nicht...

Stell dir vor, dass du im Ring stehst und dein Gegner attackiert dich. Mit jedem Schlag den du einstecken musst, überträgt dein Gegner Energie auf dich – Die Energie geht also nicht verloren, sondern bleibt erhalten. Diesen Umstand beschreibt eine Erhaltungsgleichung

Erhaltungsgleichung – Grundsätzliches

Um die Transporte von Massen, Energie oder Impulsen in technischen Systemen/ Anlagen genau beschreiben zu können, verwendet man Erhaltungsgleichungen.

Merk's dir!

Erhaltungsgleichungen sind, durch partielle Differentialgleichung gekennzeichnete, Darstellungen.

Der mathematische Umfangs solcher Berechnungen ist besonders hoch. Daher erfolgt eine Bestimmung in den meisten Fällen näherungsweise sowie numerisch.

Nachfolgend betrachten wir:

Kontinuitätsgleichung,

sowie

Impulsgleichung,

sowie

Energiegleichung

Erhaltungsgleichung – Kontinuitätsgleichung

Die Kontiniutätsgleichung, als Grundgleichung, eignet sich besonders zur Beschreibung von instationären Vorgängen in kompressiblen als auch inkompressiblen Medien.

Im Fall eines kompressiblen Mediums und unter der Annahme, dass temperaturunabhängige Stoffwerte und Konzentrationen vorliegen, gilt:

$\boxed{ \frac{\partial p}{\partial t} + \nabla (\rho \vec{v}) = 0 }$ ,

$\boxed{ \frac{\partial p}{\partial t} + \frac{\partial}{\partial x}(\rho \vec{v}_x) + \frac{\partial}{\partial y}(\rho \vec{v}_y) + \frac{\partial}{\partial z}(\rho \vec{v}_z) }$

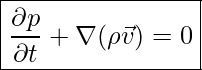
inkl. Kartesischen Koordinaten

Kennzahlen

$\boxed{t = }$ Zeit

sowie

$\boxed{\rho =}$ Dichte

sowie

$\boxed{\vec{v} = }$ Geschwindigkeit

Impulsgleichung

Die Impulsgleichung setzt die Trägheitskräfte, d. h. die zeitliche Impulsänderung und den mit der Strömung mitgeführten Impuls, mit den Druckkräften, der Schwerkraft und gegebenenfalls der Zähigkeitskraft ins Gleichgewicht. In der allgemeinen Form gilt:

$\boxed{ \frac{\partial}{\partial t} (p \vec{v}) + \nabla p \vec{v} \vec{v} = - \nabla p + p \vec{g} + \vec{X} }$

Kennzahlen:

$\boxed{ g = }$ Erdbeschleunigung

sowie

$\boxed{X =}$ Äußere Kräfte

sowie

$\boxed{p = }$ Druck

Gilt 1:

$\boxed{ \vec{X} = 0 }$ – so erhalten wir die Eulersche Gleichung.

Gilt 2:

$\boxed{ \vec{X} = \eta \nabla^2 \vec{v} }$ – so liegt die Navier-Stokes-Gleichung vor, zumal die Zähigkeit des Fluids mit $\eta$ berücksichtigt wird.

Impulsgleichungen für drei Richtungen

In kartesischen Koordinaten (drei Richtungen) formulieren wir dann folgende drei Impulsgleichungen:

Impulsgleichung – in X-Richtung, dann gilt:

$\boxed{ \frac{\partial}{\partial t} (\rho \vec{v}_x) + \frac{\partial}{\partial x} (\rho v_x v_x) + \frac{\partial}{\partial y} (\rho v_x v_y) + \frac{\partial}{\partial z} (\rho v_x v_z) = - \rho g_x - \frac{\partial p}{\partial x} + X_x }$

Impulsgleichung – in Y-Richtung, dann gilt:

$\boxed{ \frac{\partial}{\partial t} (\rho \vec{v}_y) + \frac{\partial}{\partial y} (\rho v_y v_x) + \frac{\partial}{\partial y} (\rho v_y v_y) + \frac{\partial}{\partial z} (\rho v_y v_z) = - \rho g_y - \frac{\partial p}{\partial y} + X_y }$

Impulsgleichung – in Z-Richtung, dann gilt:

$\boxed{ \frac{\partial}{\partial t} (\rho \vec{v}_z) + \frac{\partial}{\partial x} (\rho v_z v_x) + \frac{\partial}{\partial y} (\rho v_z v_y) + \frac{\partial}{\partial z} (\rho v_z v_z) = - \rho g_z - \frac{\partial p}{\partial z} + X_z }$

Energiegleichung

Nun stellen wir im letzten Schritt die Energiegleichung auf:

$\boxed{ \frac{\partial}{\partial t} (\rho ( u + \frac{v^2}{2})) + \nabla \rho \vec{v} (u + \frac{v^2}{2}) = - \nabla \rho \vec{v} + \nabla \lambda \nabla T + \dot{Q} + \rho \vec{v} \vec{g} }$

Terme – Erläuterung

Hinter den Termen rechts vom Gleichheitszeichen stecken Größen, die wir dir nachfolgend aufgelistet haben:

$\boxed{ - \nabla \rho \vec{v} = }$ Differentielle Arbeit $pdv$

sowie

$\boxed{\nabla \lambda \nabla T =}$ Wärmeübertragung durch die Leitung

sowie

$\boxed{\dot{Q} =}$ Wärmequelle oder Wärmesenke [jeweils volumetrische]

sowie

$\boxed{\rho \vec{v} \vec{g} = }$ Potentielle Energie

Eine Vereinfachung dieser Gleichung stellt die nachfolgende partielle Differentialgleichung für den Wärmetransport dar:

$\boxed{ \rho c (\frac{\partial T}{\partial t} + v_x \frac{\partial T}{\partial x} + v_y \frac{\partial T}{\partial y} + v_z \frac{\partial T}{\partial z}) = \lambda \cdot (\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}) + \dot{Q} }$

Erläuterung der Energiegleichung

Auf der linken Seite vom Gleichheitszeichen sind die Änderung der inneren Energie im Zeitverlauf sowie der Energietransport durch Mitführung in der Strömung bilanziert.

sowie

Auf der rechten Seite vom Gleichheitszeichen hingegen sind finden sich der Energietransport durch Wärmeleitung sowie die gegebene Wärmequelle/-senke wieder.

sowie

Selbst jetzt ist die Berechnung einzelner Größen noch äußerst umfangreich. Daher führen wir im kommenden Kurstext einfache Bilanzgleichungen ein.

Wir unterscheiden dabei

Bilanzgleichungen für Mengenbilanzen von
Bilanzgleichungen für Energiebilanzen.

wie gehts weiter

Wie geht's weiter?

Nachdem wir dir jetzt die Erhaltungsgleichung vorgestellt haben, folgen im nächsten Kurstext die Bilanzgleichungen.

Was gibt es noch bei uns?

Finde die richtige Schule für dich!

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe.de?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Interaktive Übungsaufgaben

Quizfrage 1

Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?

Auszüge aus unserem Kursangebot

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

ENT3 (Energetische Berechnungen) und
TM1 (Technische Mechanik – Statik) an.

Perfekte Prüfungsvorbereitung für nur 19,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 22 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 8,90 EUR/Monat
++ Besser geht’s nicht!! ++