PH1 – Einheiten umrechnen [Definition, Umrechnung, 4 Beispielaufgaben]

In dieser Lerneinheit zeigen wir dir, wie das Einheiten umrechnen funktioniert, welches innerhalb der Physik notwendig ist, damit du am Ende das richtige Ergebnis mit der richtigen Einheit erhältst.

Für ein optimales Verständnis helfen dir ein Videoclip und vier Beispiele zu dem Thema Einheiten umrechnen.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH1-Grundlagen der Physik.

Einheiten umrechnen – Überblick

In dieser Lerneinheit schauen wir uns das sehr wichtige Thema Einheiten umrechnen an. Für beinahe jeden Bereich deines Studiums benötigst du die Fähigkeit Einheiten und besonders SI-Einheiten in andere Einheiten umzurechnen.

SI-Einheiten umrechnen — Einheiten umrechnen

Nachdem du die Übersicht über die SI-Einheiten kennst und sicher immer mal wieder auf die Tabellen zurückgreifen wirst, ist es außerdem wichtig, dass du weißt wie gegebene Einheiten in SI-Einheiten umgerechnet werden.

Für die späteren Berechnungen müssen die Einheiten der einzelnen Größen zusammenpassen, damit diese gekürzt oder zusammengefasst werden können.

Zunächst zeigen wir dir die wichtigsten Umrechnungen in Tabellenform auf. Am Ende des Textes findest du einige Beispiele zur Umrechnung von Einheiten.

Einheiten umrechnen – Längen-, Zeit- und Gewichtseinheiten – Tabelle

Längeneinheiten werden zur Angaben von Entfernungen (Weg, Strecke, Abstände) verwendet. Die Basiseinheit ist das Meter (m). Die gängigen Einheiten sind hier Kilometer, Meter, Dezimeter, Zentimeter und Millimeter.

Zeiteinheiten geben die Dauer eines Ereignisses an. Die Basiseinheit ist hier die Sekunde (s). Gängig sind hier Tage (d), Stunden (h), Minuten (min) und Sekunden (s).

Gewichtseinheiten dienen zur Angabe der Masse von Körpern, also zum Beispiel dem Gewicht einer Kugel. Die Basiseinheit ist das Kilogramm (kg). Hier werden häufig Tonne (t), Kilogramm (kg) und Gramm (g) verwendet.

Gewicht - Einheiten umrechnen — Gewicht – Einheiten umrechnen

Die Umrechnungen in die SI-Einheiten siehst du in der folgenden Tabelle:

Bezeichnung	SI-Einheit	Umrechnungen in die SI-Einheit
Länge	Meter	1 km = 1.000 m 1 dm = 0,1 m 1cm = 0,01 m 1mm = 0,001 m
Zeit	Sekunde	1 d = 86.400 s 1 h = 3.600 s 1 min = 60 s
Gewicht	Kilogramm	1 t = 1.000 kg 1 g = 0,001 kg

Einheiten umrechnen – Flächen- und Volumeneinheiten – Tabelle

Aus der Basiseinheit Meter können die Flächen- und Volumeneinheiten abgeleitet werden. Hierbei ist die abgeleitete Größe für die Fläche der Quadratmeter (m²) und für das Volumen der Kubikmeter (m³).

Flächeneinheiten werden zur Angabe über die Größe einer Fläche, wie zum Beispiel der Fläche eines Dreiecks oder der Fläche eines Grundstücks, verwendet. Die Angabe erfolgt häufig in Quadratmeter (m²), Quadratzentimeter (cm²) oder Quadratmillimeter (mm²).

Volumeneinheiten geben an wie groß das Volumen eines Körpers ist, wie zum Beispiel das Volumen einer Flasche oder eines Tanks. Die Angabe erfolgt hier üblicherweise in Kubikmeter (m³), – dezimeter (dm³), -zentimeter (cm³) oder -millimeter (mm³) sowie in Liter (l).

Volumeneinheiten, Flächeneinheiten, Längeneinheiten, Einheiten umrechnen — Volumen – Einheiten umrechnen

In der nachfolgenden Tabelle siehst du wie die Flächen- und Volumeneinheiten in die SI-Einheiten umgerechnet werden: die

Bezeichnung

abgleitete SI-Einheit

Umrechnungen in die abgeleitete SI-Einheit

Fläche

Quadratmeter

1 dm² = 0,01 m²

1 cm² = 0,0001 m²

1 mm² = 0,000001 m² = 1⋅ 10^-6

Volumen

Kubikmeter

1 l = 1 dm³ = 0,001m³

1 cm³ = 0,000001 m³ = 1⋅ 10^-6

1 mm³ = 0,000000001 m³ = 1⋅ 10^-9

Einheiten umrechnen – Die weiteren Basiseinheiten – Tabelle

Weitere Basiseinheiten sind

Ampere (A) für die elektrische Stromstärke, welche auch in Kiloampere (kA) oder Milliampere (mA) angegeben wird,
Kelvin (K) für die Temperatur, welche auch in Grad Celsius (°C) oder Grad Fahrenheit (°F) angegeben wird,
Candela (cd) für die Lichtstärke, welche grundsätzlich nur in Candela angegeben wird und
Mol (mol) für die Angabe einer Stoffmenge, welche auch in Megamol (Mmol), Kilomol (kmol), Millimol (mmol), Mikromol (µmol) und Nanomol (nmol) angegeben wird.

Temperatur, Celsius, Kelvin, Einheiten umrechnen — Temperatur, Celsius, Kelvin – Einheiten umrechnen

Die Umrechnungen der obigen Einheiten in die SI-Einheiten ist in der nachfolgenden Tabelle dargestellt:

Bezeichnung	SI-Einheit	Umrechnungen in die abgeleitete SI-Einheit
Elektrische Stromstärke	Ampere (A)	1 kA = 1.000 A 1 mA = 0,001 A
Temperatur	Kelvin (K)	0 °C = 273,15 K 23 °F = 273,15 K
Lichtstärke	Candela (cd)	–
Stoffmenge	Mol (mol)	01 Mmol = 1 Mio mol n1 kmol = 1.000 mol v1 mmol = 0,001 mol 61 µmol = 0,000001 mol = 1⋅ 10^-6 mol 1 nmol = 1⋅ 10^-9 mol

Einheiten umrechnen: Winkeleinheit

Eine Winkeleinheit ist das Maß für die Größe eines Winkels. Es gibt die unterschiedlichsten Möglichkeiten die Größe eines Winkels anzugeben wie u.a. Grad, Gon und Radiant.

Die bekannteste Winkeleinheit ist das Grad (°), welches schon im alten Babylon verwendet wurde. Beim Grad besitzt der Vollkreis 360°, ein Halbkreis 180° und ein Viertelkreis bzw. der rechte Winkel 90°.

Bei der Einheit Gon (gon) hat der Vollkreis 400 gon, der Halbkreis 200 gon und der Viertelkreis bzw. rechte Winkel 100 gon. Diese Einheit hat sich aber nicht durchgesetzt.

Das Radiant (rad) oder auch das Bogenmaß ist die SI-Einheit für die Größe eines Winkels. Beim Winkelmaß Radiant gibt man den Winkel als Länge des Kreisbogens an, und zwar für einen Kreis mit Radius r = 1. Dadurch hat ein Vollkreis genau 2π rad, ein Halbkreis π rad und ein Viertelkreis bzw. rechter Winkel π/2 rad.

Winkel umrechnen, Einheiten umrechnen — Winkel – Einheiten umrechnen

Der Winkel wird aber häufig nicht in Radiant angegeben, sondern in Grad, weshalb du die Umrechnung in jedem Fall kennen solltest:

Bezeichnung

SI-Einheit

Umrechnungen in die SI-Einheit

Winkel

Radiant (rad)

1 ° = π/180 rad

1 rad = 180/π °

Alle weiteren Einheiten wie zum Beispiel Newton, Watt oder Joule setzen sich aus den obigen Einheiten zusammen.

Videoclip: Abgleitete Einheiten umrechnen

Im folgenden Video zeigen wir dir die Längen-, Flächen- und Volumeneinheiten sowie die Winkeleinheiten auf.

Lernclip

Längen-, Flächen-, Volumen- und Winkeleinheiten

Schauen wir uns mal einige Beispiele zum Umrechnen von Einheiten an.

Beispiele: Einheiten umrechnen

In den nachfolgenden Beispielen schauen wir uns mal an, wie Einheiten umgerechnet werden. Das Umrechnen von Einheiten ist eine Grundvoraussetzung bei der späteren Berechnung von Aufgaben innerhalb der Physik. Du solltest diese Fertigkeit in jedem Fall beherrschen, da ansonsten Berechnungsfehler auftreten können.

Beispiel 1: Einheiten umrechnen: Zusammenfassen

Gegeben sei eine Kiste mit dem Gewicht von 2.000 g. Du sollst die Gewichtskraft dieser Kiste angeben.

Die Gewichtskraft $F_G$ wird wie folgt bestimmt:

$F_G = m \cdot g$

Hierbei ist $m$ die Masse, also das Gewicht und g die Erdbeschleunigung. Die Erdbeschleunigung ist eine Konstante mit $g = 9,81 \frac{m}{s^2}$ . Du musst nun also die Masse und Erdbeschleunigung miteinander multiplizieren, um die Gewichtskraft berechnen zu können.

$F_G = 2.000 g \cdot 9,81 \dfrac{m}{s^2} = 19.620 g \dfrac{m}{s^2}$

Für die Berechnung kannst du nicht einfach Gramm einsetzen, da dies nicht die SI-Einheit der Masse ist. Die SI-Einheit ist Kilogramm. Du musst also zunächst Gramm in Kilogramm umrechnen und kannst dann die Berechnung durchführen:

$F_G = 2 kg \cdot 9,81 \dfrac{m}{s^2} = 19,62 \dfrac{kg \; m}{s^2} = 19,62 N$

Du erhältst hieraus die abgeleitete Einheit Newton mit $N = \dfrac{kg \; m}{s^2}$ . In diesem Beispiel hast du die Einheiten zu einer neuen Einheit zusammengefasst.

Beispiel 2: Einheiten umrechnen: Kürzen von Einheiten

Ein weiteres Beispiel zeigt auf, dass die Einheiten auch gekürzt werden können:

Eine Kraft $F$ mit dem senkrechten Abstand von 10 cm zu einem Punkt A übt ein Drehmoment von $M = 240 Nm$ auf den Punkt A aus.

Wie groß ist die Kraft $F$ ?

Ein Moment ist die Drehwirkung einer Kraft auf einen bestimmten festgelegten Punkt und wird wie folgt berechnet:

$M = F \cdot h$

Hierbei ist $F$ die Kraft in Newton und $h$ der senkrechte Abstand (auch: Hebelarm) in Meter. Wir wollen aus dieser Gleichung die Kraft berechnen und stellen nach $F$ um:

$F = \dfrac{M}{h}$

Wir können nun aber nicht einfach $M = 240 Nm$ und $h = 10 cm$ einsetzen. Wir müssen die Längenangabe in Meter umrechnen:

$10 cm = 0,1 m$

Einsetzen:

$F = \dfrac{240 Nm}{0,1m} = 2.400 N$

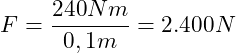
In diesem Beispiel kürzt sich das Meter heraus und verbleibt Newton, welches die Einheit einer Kraft ist.

Beispiel 3: Einheiten umrechnen: Einheiten als Bruch

Du musst natürlich ebenfalls wissen, wie man Einheiten umrechnet, die als Bruch dargestellt sind.

Die Dichte einer Flüssigkeit oder eines Körpers ist nichts anderes als die Masse eines Körpers durch sein Volumen:

$\rho = \dfrac{m}{V}$

Die abgeleitete SI-Einheit ist also Kilogramm (für die Masse) durch Kubikmeter (für das Volumen). Die Dichte wird aber häufig in g/cm³ oder kg/dm³ oder auch kg/l angegeben. Ist dies der Fall, so musst du wissen, wie du diese Einheit so umrechnest, dass kg/m³ resultiert.

Schauen wir uns dazu mal ein Beispiel zur Dichte an.

Gegeben sei die Dichte von Wasser mit $0,997 \dfrac{g}{cm^3}$ .

Gebe die Dichte in kg/m³ an!

Bei dieser Angabe ist sowohl der Zähler als auch der Nenner nicht gemäß der SI-Einheiten. Für den Zähler muss kg gelten und für den Nenner m³. Du kannst nun beiden Berechnungen separat durchführen und danach mit der Zahl davor multiplizieren:

Zähler: $1 g = 0,001 kg$

Nenner: $1 cm^3 = 0,000001 m^3$

Dein neuer Einheitenbruch sieht also wie folgt aus:

$0,997 \; \dfrac{0,001 kg}{0,000001 m^3}$

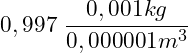
Die Zahlen kannst du nach vorne holen:

$0,997 \; \dfrac{ 0,001}{0,000001} \; \dfrac{kg}{ m^3}$

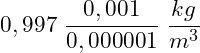
Und dann berechnest du den Zahlenbruch und multiplizierst das Ergebnis mit der Zahl davor:

$0,997 \cdot 1.000 \; \dfrac{kg}{ m^3}$

$997 \; \dfrac{kg}{ m^3}$

Und schon hast du die Dichte so gegeben, dass diese innerhalb von Berechnungen eingesetzt werden kann.

Beispiel 4: Einheiten umrechnen: Winkeleinheiten

Zum Schluss wollen wir uns noch ein Beispiel für die Umrechnung von Winkeleinheiten anschauen.

Gegeben sei der Winkel 132°. Rechne diese in Radiant, also Bogenmaß, um!

Aus der Tabelle weiter oben auf der Seite entnehmen wir:

$1^\circ = \dfrac{\pi}{180^\circ} rad$

Wir haben nun aber 132°, also gilt:

$132^\circ = 132 \dfrac{\pi}{180^\circ } rad$

$132^\circ = 2,30 rad$

Die Länge des Kreisbogens von 0° bis 132° beträgt 2,3 Radiant. Die Länge des Kreisbogens ist abhängig vom Radius. Ist ein Radius von 5 cm gegeben, so ist die Länge des Kreisbogens in Radiant mit dem Radius des Kreises zu multiplizieren, um die genaue Länge angeben zu können:

$5cm \cdot 2,3 rad = 11,5 cm$ .

Der Kreisbogen ist in diesem Fall 11,5 cm lang.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++