[INFO3] Probekurs – Einblick in unser Lernsystem [INFO3] TM2 – Ebener Spannungszustand – Spannungstransformation

Kapitel 12 von 44

Daran arbeitest Du

← Zurück Weiter→

[INFO3] TM2 – Ebener Spannungszustand – Spannungstransformation

dein_dozent_jan

Dieser Kurstext ist ein Auszug aus unserem Onlinekurs: TM2 – Festigkeitslehre

In dieser Lerneinheit betrachten wir den ebenen Spannungszustand sowie die Formeln zur Transformation des ebenen Spannungszustandes.

Ebener Spannungszustand

Ein ebener Spannungszustand ist dann gegeben, wenn innerhalb eines dreidimensionalen Bauteils die Spannungen nur in in zwei Raumrichtungen auftreten.

Ein ebener Spannungszustand liegt zum Beispiel näherungsweise in Scheiben vor.

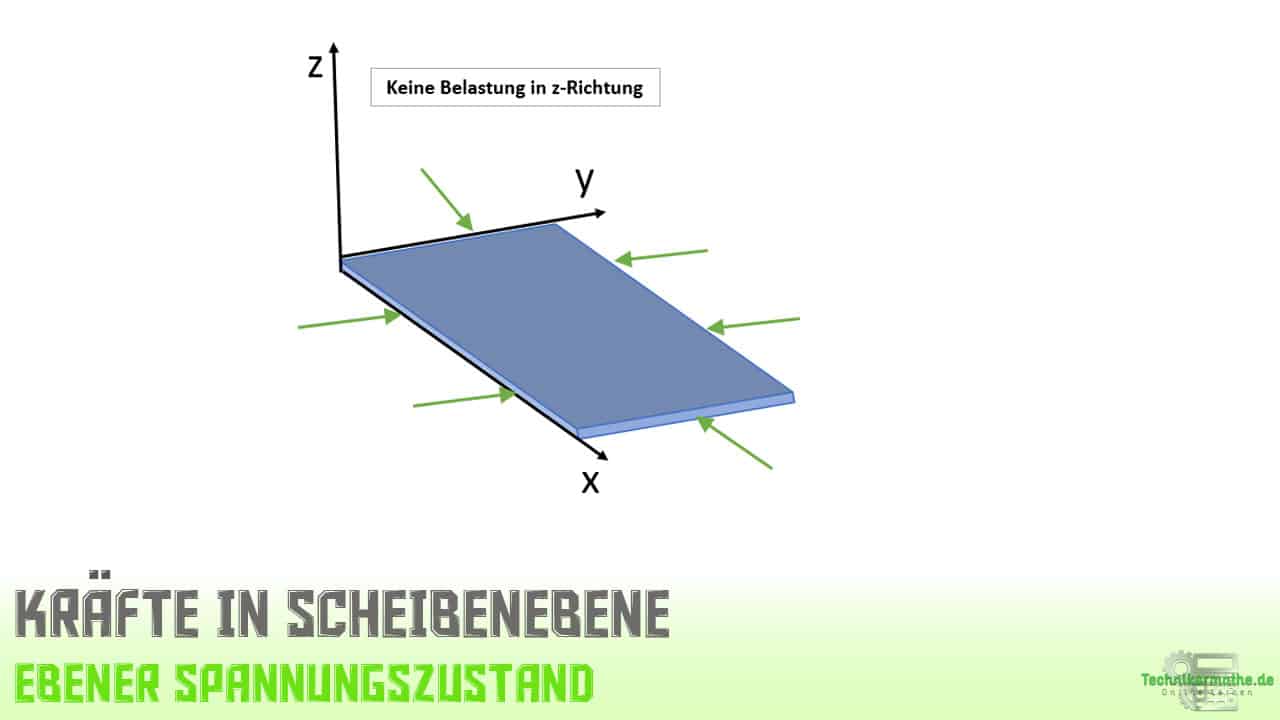
Scheibe, ebener Spannungszustand

Eine Scheibe ist dadurch gekennzeichnet, dass ihre Dicke klein gegenüber den übrigen Abmessungen ist und dass sie nur in der x,y-Ebene belastet wird. Das bedeutet, dass die Spannungen, Verzerrungen und Verschiebungen nur von den x und y Koordinaten abhängen.

Dadurch, dass die Scheibe nur in der x,y-Ebene belastet wird, sind die Spannungen in der z-Richtung gleich Null:

$\sigma_z = 0$

$\tau_{xz} = \tau_{zx} = 0$

$\tau_{yz} = \tau_{zy} = 0$

Der Spannungstensor S reduziert sich im ebenen Spannungszustand auf 3 Spannungskomponenten:

$S = \begin{pmatrix} \sigma_x & \tau_{xy} \\ \tau_{yx} & \sigma_y \end{pmatrix}$

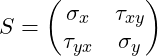
mit

$\tau_{xy} = \tau_{yx}$

Die Spannungen σ_x, σ_y und τ_xy sind diejenigen Spannungen, die in den Schnitten parallel zu den Koordinatenachsen auftreten. Schneiden wir also ein Stück so aus der Scheibe heraus, dass die Schnitte parallel zu den Koordinatenachsen sind, so erhalten wir die Spannungen wie folgt:

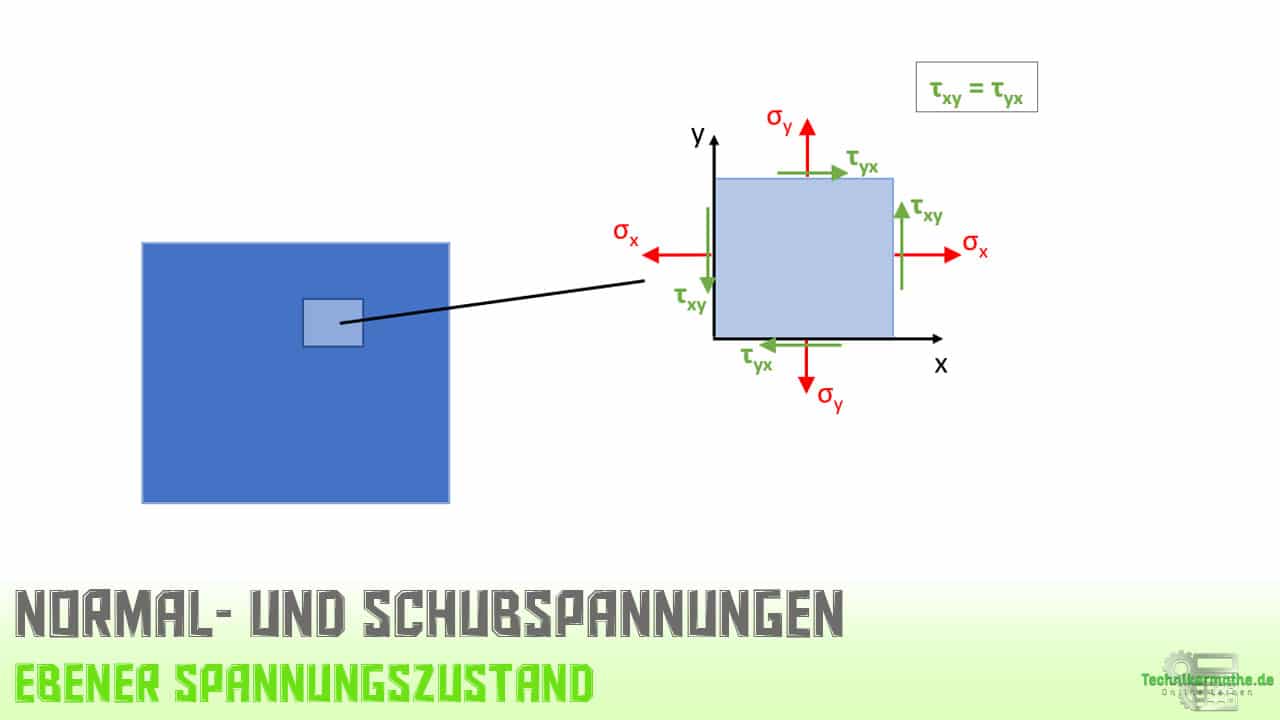
Spannungen, ebener Spannungszustand

Wir gehen im Folgenden davon aus, dass die obigen Spannungen für Schnitte parallel zu den Koordinatenachsen bekannt sind. Wir können aus diesen gegebenen Spannungen dann auch diejenigen Spannungen berechnen, die nicht in Richtung der Koordinatenachsen zeigen, die also nicht in Schnitten auftreten, die parallel zu den Koordinatenachsen sind.

Video: Spannungstransformation

Im folgenden Videoclip zeigen wir dir, was genau die Spannungstransformation des ebenen Spannungszustand bedeutet und welche Formeln du hierfür benötigst.

Spannungstransformation

Wir wollen uns jetzt anschauen, wie wir die Spannungen berechnen die bei einem Schnitt durch das Bauteil auftreten, welcher nicht parallel zu den Koordinatenachsen ist.

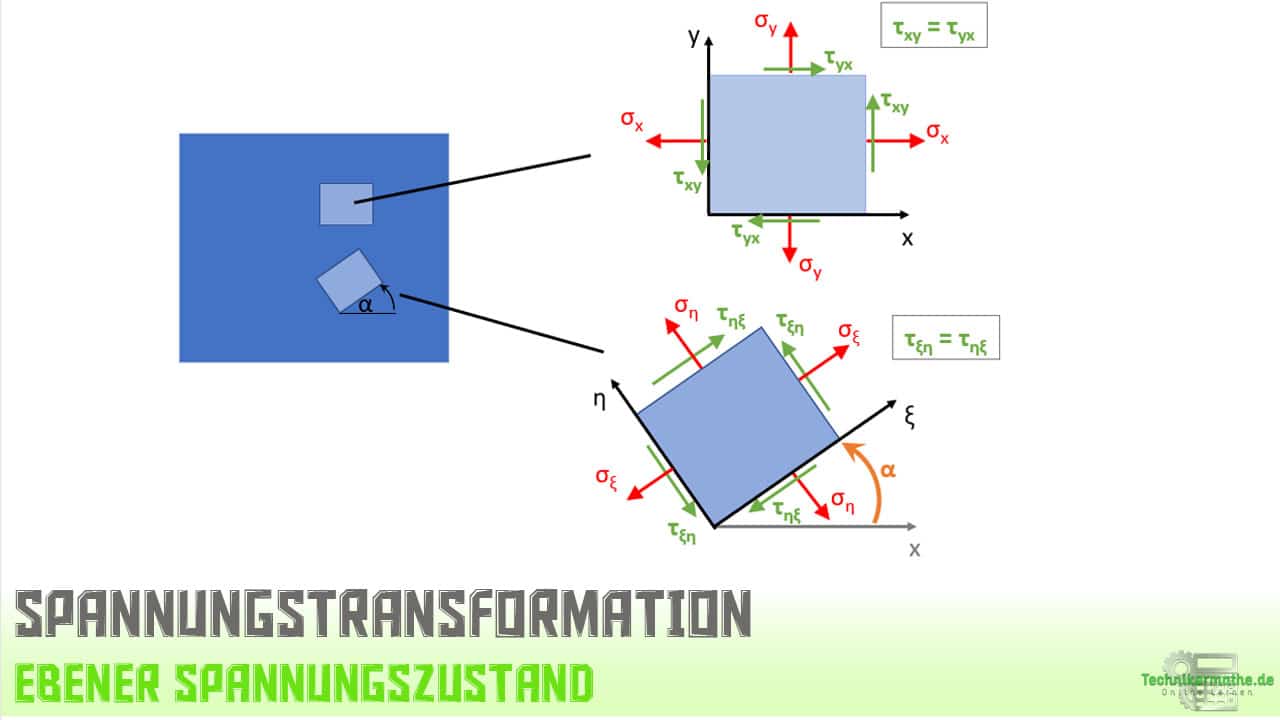
Spannungstransformation, ebener Spannungszustand, Koordinatentransformation

In der obigen Grafik betrachten wir zum einen ein herausgeschnittenes ebenes Element, für welches die Schnitte parallel zu den x,y-Achsen liegen und zum anderen ein herausgeschnittenes Element, für welches die Schnitte nicht parallel zu den x,y-Achsen liegen.

Für das untere herausgeschnittene Element können wir neue Koordinatenachsen einführen und legen diese parallel zu den Schnittflächen. Die Beschriftung der Koordinatenachsen haben wir hier beliebig mit ξ (griechischer Buchstabe Xi) und η (griechischer Buchstabe Eta) gewählt.

Für das untere Element treten Normal- und Schubspannungen auf. Die Normalspannungen σ_ξ und σ_η stehen senkrecht auf den Schnittflächen, die Schubspannungen τ_ξη und τ_ηξliegen parallel zu den Schnittflächen.

Der Winkel α gibt die Drehung des Elements ausgehend von der x-Achse an.

Wir gehen davon aus, dass die Spannungen σ_x, σ_y sowie τ_xy für die Schnitte parallel zu den Koordinatenachsen bekannt sind.

Formeln für die Spannungstransformation

Mit den gegebenen Spannungen σ_x, σ_yund τ_xy sowie dem Winkel α können wir die unbekannten Spannungen σ_ξ, σ_ηundτ_ξη berechnen. Dazu können wir die folgenden Formeln heranziehen:

$\boxed{\sigma_{\xi} = \dfrac{\sigma_x + \sigma_y}{2} + \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) + \tau_{xy} \cdot \sin(2 \alpha)}$

$\boxed{\sigma_{\eta} = \dfrac{\sigma_x + \sigma_y}{2} - \dfrac{\sigma_x - \sigma_y}{2} \cdot \cos(2 \alpha) - \tau_{xy} \cdot \sin(2 \alpha)}$

$\boxed{\tau_{\eta \xi} = \tau_{\xi \eta} = - \dfrac{\sigma_x - \sigma_y}{2} \cdot \sin(2 \alpha) + \tau_{xy} \cdot \cos(2 \alpha)}$

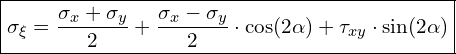
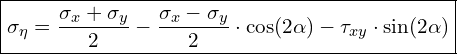
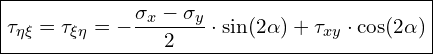
Außerdem gelten:

$\boxed{\sigma_x + \sigma_y = \sigma_{\xi} + \sigma_{\eta} }$ 1. Invariante

$\boxed{\sigma_x \cdot \sigma_y - \tau_{xy} = \sigma_{\xi} \cdot \sigma_{\eta} - \tau_{\xi \eta}}$ 2. Invariante

Für die obigen Formeln gilt die folgende Ausgangsituation für positive Spannungen:

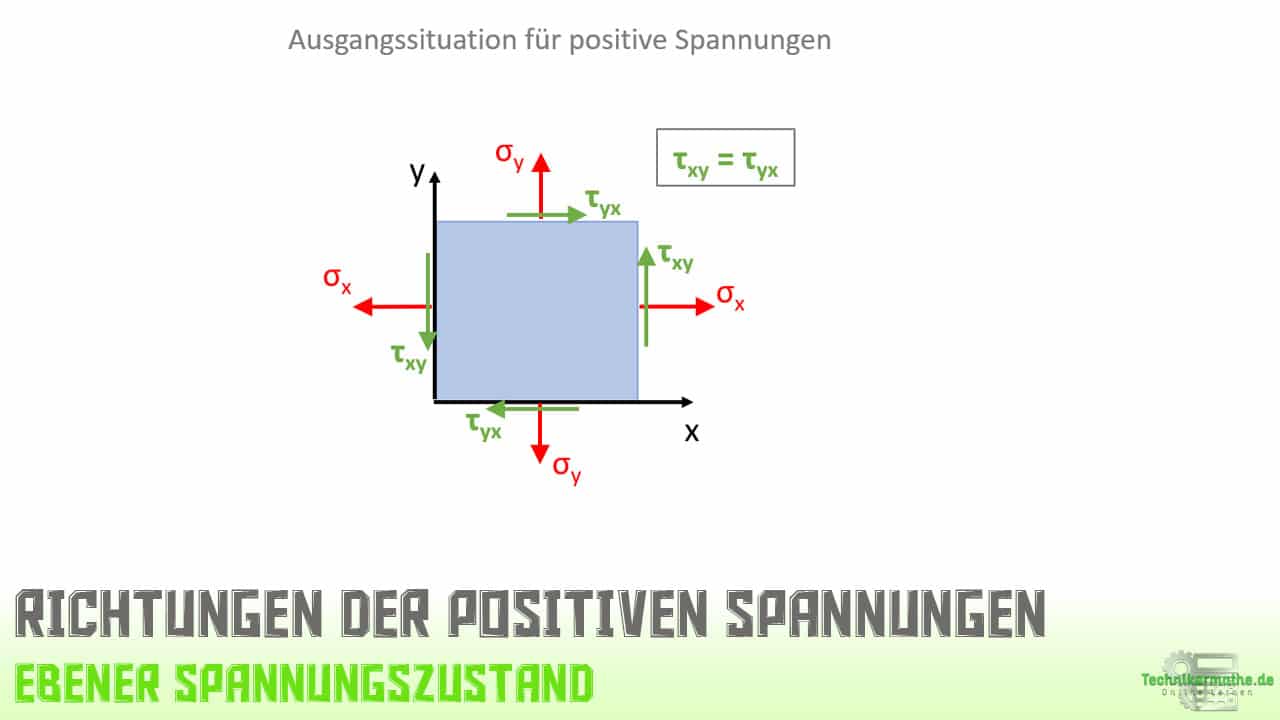
Koordinatentransformation, ebener Spannungszustand, Spannungstransformation

Sind positive Spannungen gegeben, so wirken diese in die oben gezeigten Richtungen. Bei negativen Spannungen wirken diese genau entgegengesetzt (um 180° gedreht). Die obigen Formeln gelten für positive Spannungen, sind also negative Spannungen gegeben, so müssen diese innerhalb der Formel mit einem Minuszeichen berücksichtigt werden.

Der Winkel α wird dann positiv berücksichtigt, wenn die Drehung des Ausgangskoordinatensystems in einer Linksdrehung (gegen den Uhrzeigersinn) erfolgt und negativ, wenn ein Rechtsdrehung (mit dem Uhrzeigesinn) des Ausgangskoordinatensystems stattfindet.

Schnittwinkel vs. Drehwinkel

Wenn wir aus einem ebenen Bauteil (z.B. einer Scheibe) ein Stück herausschneiden und die Spannungen abtragen, dann können wir entweder wie oben den Drehwinkel α im Bezug zum Ausgangskoordinatensystem angeben oder aber den Schnittwinkel β unter welchem der Schnitt durchgeführt wird:

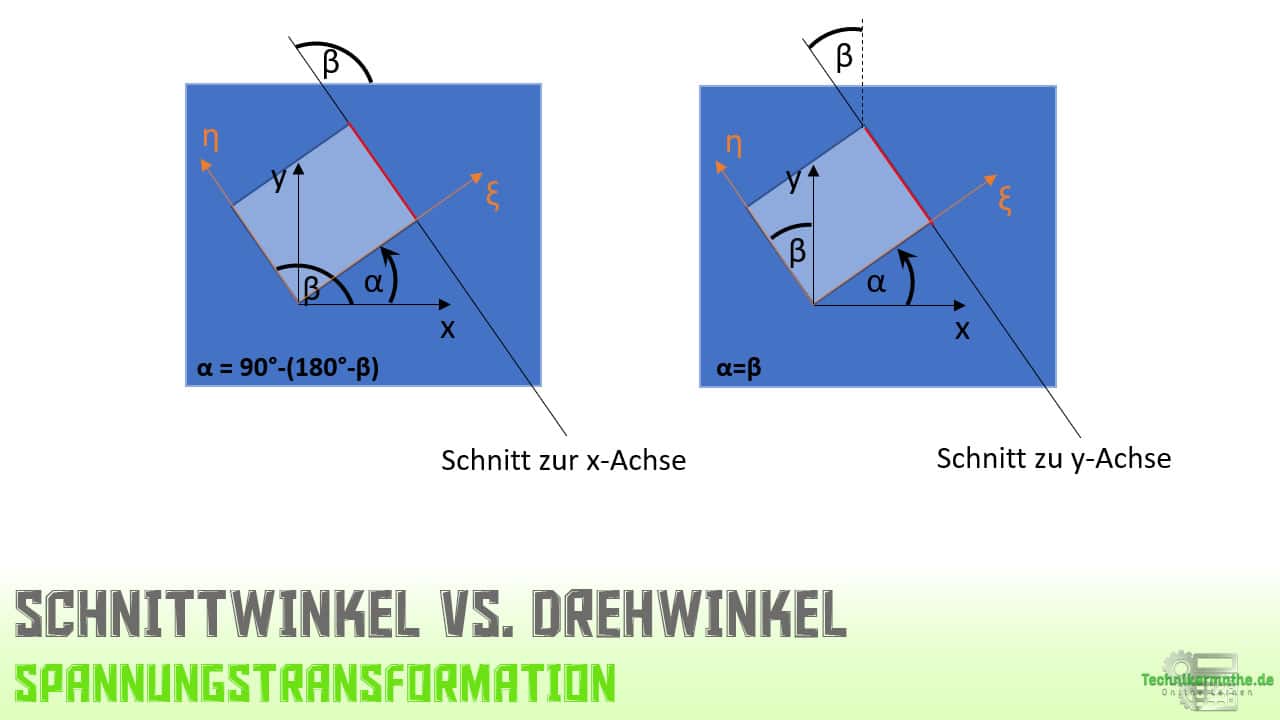
Spannungstransformation, ebener Spannungszustand, Schnittwinkel

In der obigen Grafik unterscheiden wir zwischen einem Schnittwinkel zur x-Achse und einem Schnittwinkel zur y-Achse. Je nachdem zu welcher Achse der Schnitt erfolgt, ergeben sich unterschiedliche Drehungen des Ausgangskoordinatensystems und damit unterschiedliche Drehwinkel.

Ist in der Aufgabe der Schnittwinkel β gegeben, so kannst du den Drehwinkel α, welchen du für die obigen Formeln benötigst, wie folgt berechnen:

Schnittwinkel zur x-Achse:

$\boxed{\alpha = 90^\circ - (180^\circ - \beta)}$

Schnittwinkel zur y-Achse:

$\boxed{\alpha = \beta}$

In der folgenden Lerneinheit schauen wir uns eine Aufgabe an, in welcher du die Anwendung der obigen Formeln erlernst.

[INFO3] Probekurs - Einblick in unser Lernsystem

Physik 1 (PH1) - Grundlagen der Physik