In dieser Lerneinheit behandeln wir die Schnittmenge von Mengen. Die Schnittmenge wird auch häufig als Durchschnitt von Mengen bezeichnet.
Für ein optimales Verständnis helfen dir zwei Videoclips und mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: Ma1-Grundlagen der Mathematik Auch interessant! Alles zu Linearen Gleichungen findest du im Kurs: Ma2-Lineare Gleichungssysteme

Schnittmengen | Grundlagen
Die Schnittmenge zweier Mengen A und B sind alle Elemente, die in der Menge A und in der Menge B enthalten sind.
Was ist eine Schnittmenge?
Die Schnittmenge zweier Mengen enthält alle Elemente, die in beiden Mengen gleichzeitig vorhanden sind. Diese Operation hilft, die gemeinsamen Elemente zwischen zwei oder mehr Mengen zu identifizieren.
Schnittmenge – Schreibweise
Das Zeichen für die Angabe der Schnittmenge bzw. der Durchschnitt von Mengen ist:
Ist also eine Menge A Schnittmenge der Menge B, so schreiben wir:
A geschnitten mit B
Wir können das ganze aber auch in beschreibender Mengenschreibweise wie folgt angeben:
Gelesen: A geschnitten mit B ist gleich die Menge aller x für die gilt: x ist Element von A und () Element von B.
Das -Zeichen ist das logische UND und bedeutet, dass beide Aussagen (die links und die rechts) erfüllt sein müssen, damit die gesamte Aussage erfüllt (wahr) ist.
Venn-Diagramm | Beschreibende Mengenschreibweise | Darstellung
In der nachfolgenden Grafik siehst du die Schnittmenge nochmal als Venn-Diagramm und in der beschreibenden Mengenschreibweise angegeben:
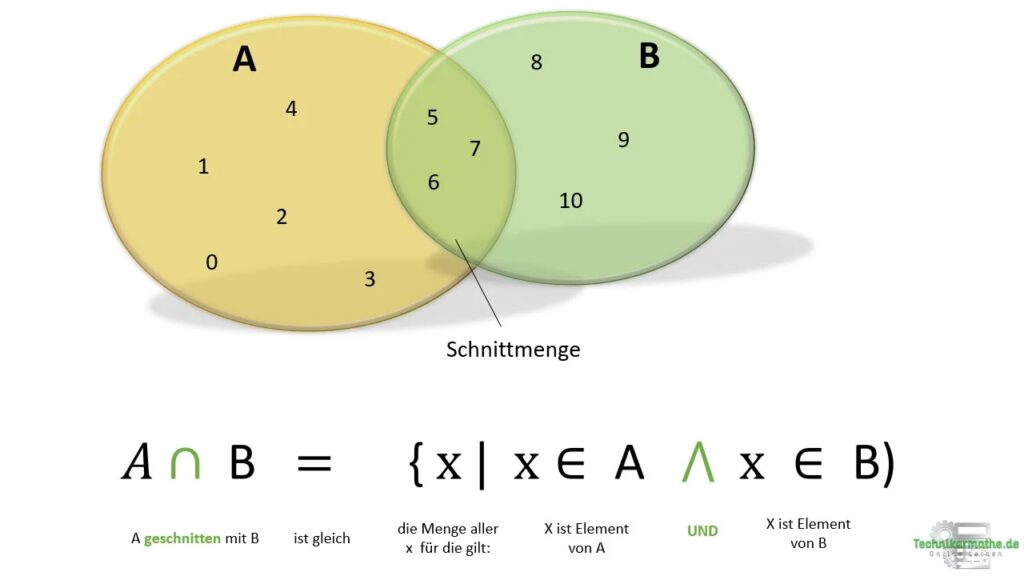
Im Venn-Diagramm ist die Schnittmenge der beiden Mengen genau der Bereich, bei welchem sich die Flächen der beiden Kreise überschneiden.
++ Videoclip – Schnittmengen ++
Im folgenden Video zeigen wir dir anhand eines Beispiels, wie du die Schnittmenge zweier Mengen bildest.
Schauen wir uns im folgenden mal einige Beispiele zur Schnittmenge zweier Mengen an.
Beispiele zur Schnittmenge
Beispiel 1 : Schnittmengen / Durchschnitt von Mengen
Gegeben seien die beiden Mengen A = {-4, -2, 0, 4, 5, 8, 10} und B = {-1, -2, 0, 8, 9, 10 }.
Bestimme !
Die Schnittmenge bzw. der Durchschnitt zweier Mengen A und B sind alle Elemente, die in der Menge A UND in der Menge B enthalten sind.
Die Schnittmenge bzw. der Durchschnitt der beiden Mengen enthält drei Elemente.
Beispiel 2: Schnittmengen / Durchschnitt von Mengen
Gegeben seien die beiden Mengen und
.
Bestimme !
Die Schnittmenge zweier Mengen A und B sind alle Elemente, die in der Menge A UND in der Menge B enthalten sind. Die Menge B ist als beschreibende Mengenschreibweise angegeben. Da es sich hierbei um die ganzen Zahlen handelt, können wir diese auch in aufzählender Mengenschreibweise angeben:
Wir können nun die gemeinsamen Elemente der beiden Mengen in der Schnittmenge zusammenfassen:
Beispiel 3: Schnittmengen / Durchschnitt von Mengen
Gegeben seien die beiden Mengen und
.
Bestimme bzw.
!
Die Schnittmenge ist kommutativ, d.h. .
Wir haben hier beide Mengen in beschreibender Mengenschreibweise angegeben. Für beide Mengen ist x Element der reellen Zahlen. Wir können dies Mengen nun nicht in aufzählender Mengenschreibweise angegeben, aber da sie den gleichen Zahlenbereich aufweisen miteinander vergleichen.
Menge A startet bei -10. Menge B startet bei -5.
Menge A endet bei 5. Menge B endet bei 20.
Die Zahlen dazwischen haben beide Mengen gemeinsamen, also von -5 bis 5. Wir müssen aber hier die Schnittmenge auch in beschreibender Form angegeben, da alle Zahlen zwischen -5 und 5 berücksichtigt werden (auch die Dezimalzahlen):
Anwendung der Schnittmenge
- Datenbanken: In Datenbanken wird die Schnittmenge verwendet, um Datensätze zu finden, die in mehreren Tabellen oder Abfragen gemeinsam vorkommen.
- Wahrscheinlichkeit: In der Wahrscheinlichkeitsrechnung hilft die Schnittmenge, die Wahrscheinlichkeit gemeinsamer Ereignisse zu berechnen.
- Venn-Diagramme: Venn-Diagramme visualisieren die Schnittmenge zwischen verschiedenen Mengen und zeigen gemeinsame Elemente.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist eine Schnittmenge?
Die Schnittmenge ist die Menge aller Elemente, die in beiden betrachteten Mengen gleichzeitig enthalten sind.
2. Wie berechnet man die Schnittmenge?
Man listet alle Elemente auf, die in beiden Mengen vorkommen.
3. Was passiert, wenn die Schnittmenge leer ist?
Wenn es keine gemeinsamen Elemente gibt, ist die Schnittmenge die leere Menge (∅).
4. Kann die Schnittmenge mehrerer Mengen berechnet werden?
Ja, die Schnittmenge mehrerer Mengen enthält alle Elemente, die in allen betrachteten Mengen gemeinsam sind.
Zusammenfassung
Die Schnittmenge zweier oder mehrerer Mengen enthält alle gemeinsamen Elemente. Mit Eigenschaften wie Kommutativität und Assoziativität ist das Arbeiten mit Schnittmengen in der Mathematik strukturiert und logisch. Diese Konzepte sind nicht nur theoretisch, sondern finden auch praktische Anwendung in verschiedenen Bereichen wie Datenbanken und Wahrscheinlichkeitsrechnung. Mit diesen Kenntnissen kannst du schnell und korrekt mit Schnittmengen arbeiten.
In der folgenden Lerneinheit behandeln wir die Vereinigung zweier Mengen (Vereinigungsmenge).
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






